LLMs for Supply Chain Management

The development of large language models (LLMs) has provided new tools for research in supply chain management (SCM). In this paper, we introduce a retrieval-augmented generation (RAG) framework that dynamically integrates external knowledge into the inference process, and develop a domain-specialized SCM LLM, which demonstrates expert-level competence by passing standardized SCM examinations and beer game tests. We further employ the use of LLMs to conduct horizontal and vertical supply chain games, in order to analyze competition and cooperation within supply chains. Our experiments show that RAG significantly improves performance on SCM tasks. Moreover, game-theoretic analysis reveals that the LLM can reproduce insights from the classical SCM literature, while also uncovering novel behaviors and offering fresh perspectives on phenomena such as the bullwhip effect. This paper opens the door for exploring cooperation and competition for complex supply chain network through the lens of LLMs.

New Additive OCBA Procedures for Robust Ranking and Selection

Robust ranking and selection (R&S) is an important and challenging variation of conventional R&S that seeks to select the best alternative among a finite set of alternatives. It captures the common input uncertainty in the simulation model by using an ambiguity set to include multiple possible input distributions and shifts to select the best alternative with the smallest worst-case mean performance over the ambiguity set. In this paper, we aim at developing new fixed-budget robust R&S procedures to minimize the probability of incorrect selection (PICS) under a limited sampling budget. Inspired by an additive upper bound of the PICS, we derive a new asymptotically optimal solution to the budget allocation problem. Accordingly, we design a new sequential optimal computing budget allocation (OCBA) procedure to solve robust R&S problems efficiently. We then conduct a comprehensive numerical study to verify the superiority of our robust OCBA procedure over existing ones. The numerical study also provides insights on the budget allocation behaviors that lead to enhanced efficiency.

Sample-Optimal Large-Scale Optimal Subset Selection

Ranking and selection (R&S) conventionally aims to select the unique best alternative with the largest mean performance from a finite set of alternatives. However, for better supporting decision making, it may be more informative to deliver a small menu of alternatives whose mean performances are among the top $m$. Such problem, called optimal subset selection (OSS), is generally more challenging to address than the conventional R&S. This challenge becomes even more significant when the number of alternatives is considerably large. Thus, the focus of this paper is on addressing the large-scale OSS problem. To achieve this goal, we design a top-$m$ greedy selection mechanism that keeps sampling the current top $m$ alternatives with top $m$ running sample means and propose the explore-first top-$m$ greedy (EFG-$m$) procedure. Through an extended boundary-crossing framework, we prove that the EFG-$m$ procedure is both sample optimal and consistent in terms of the probability of good selection, confirming its effectiveness in solving large-scale OSS problem. Surprisingly, we also demonstrate that the EFG-$m$ procedure enables to achieve an indifference-based ranking within the selected subset of alternatives at no extra cost. This is highly beneficial as it delivers deeper insights to decision-makers, enabling more informed decision-makings. Lastly, numerical experiments validate our results and demonstrate the efficiency of our procedures.

AlphaRank: An Artificial Intelligence Approach for Ranking and Selection Problems

We introduce AlphaRank, an artificial intelligence approach to address the fixed-budget ranking and selection (R&S) problems. We formulate the sequential sampling decision as a Markov decision process and propose a Monte Carlo simulation-based rollout policy that utilizes classic R&S procedures as base policies for efficiently learning the value function of stochastic dynamic programming. We accelerate online sample-allocation by using deep reinforcement learning to pre-train a neural network model offline based on a given prior. We also propose a parallelizable computing framework for large-scale problems, effectively combining "divide and conquer" and "recursion" for enhanced scalability and efficiency. Numerical experiments demonstrate that the performance of AlphaRank is significantly improved over the base policies, which could be attributed to AlphaRank's superior capability on the trade-off among mean, variance, and induced correlation overlooked by many existing policies.

Learning to Simulate: Generative Metamodeling via Quantile Regression

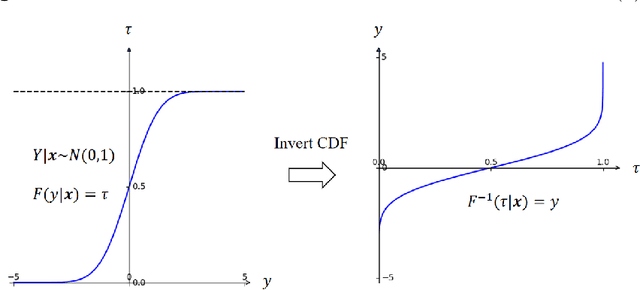
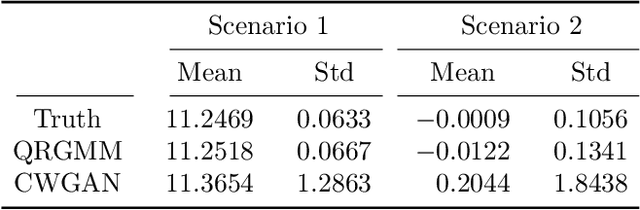
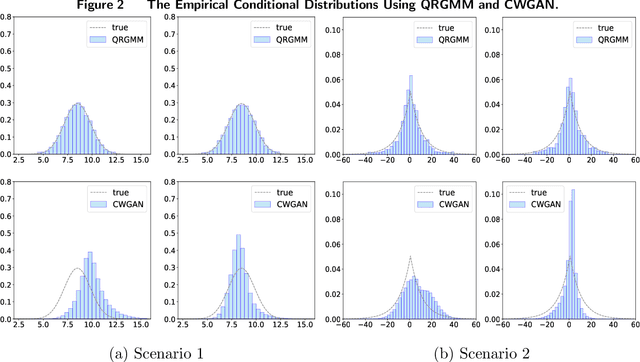
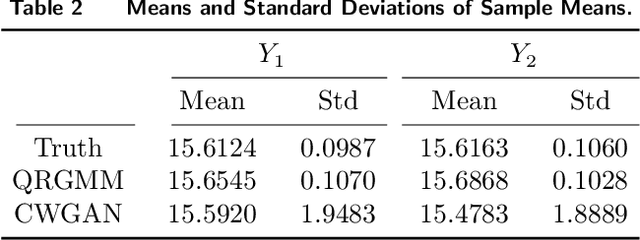
Stochastic simulation models, while effective in capturing the dynamics of complex systems, are often too slow to run for real-time decision-making. Metamodeling techniques are widely used to learn the relationship between a summary statistic of the outputs (e.g., the mean or quantile) and the inputs of the simulator, so that it can be used in real time. However, this methodology requires the knowledge of an appropriate summary statistic in advance, making it inflexible for many practical situations. In this paper, we propose a new metamodeling concept, called generative metamodeling, which aims to construct a "fast simulator of the simulator". This technique can generate random outputs substantially faster than the original simulation model, while retaining an approximately equal conditional distribution given the same inputs. Once constructed, a generative metamodel can instantaneously generate a large amount of random outputs as soon as the inputs are specified, thereby facilitating the immediate computation of any summary statistic for real-time decision-making. Furthermore, we propose a new algorithm -- quantile-regression-based generative metamodeling (QRGMM) -- and study its convergence and rate of convergence. Extensive numerical experiments are conducted to investigate the empirical performance of QRGMM, compare it with other state-of-the-art generative algorithms, and demonstrate its usefulness in practical real-time decision-making.

Large-Scale Inventory Optimization: A Recurrent-Neural-Networks-Inspired Simulation Approach

Many large-scale production networks include thousands types of final products and tens to hundreds thousands types of raw materials and intermediate products. These networks face complicated inventory management decisions, which are often too complicated for inventory models and too large for simulation models. In this paper, by combing efficient computational tools of recurrent neural networks (RNN) and the structural information of production networks, we propose a RNN inspired simulation approach that may be thousands times faster than existing simulation approach and is capable of solving large-scale inventory optimization problems in a reasonable amount of time.

Dimension Reduction in Contextual Online Learning via Nonparametric Variable Selection

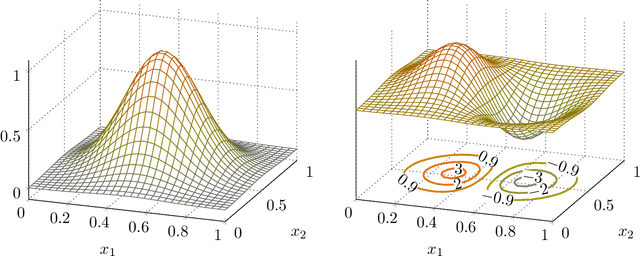
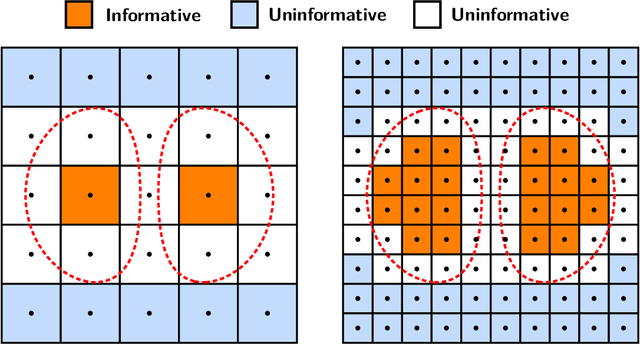
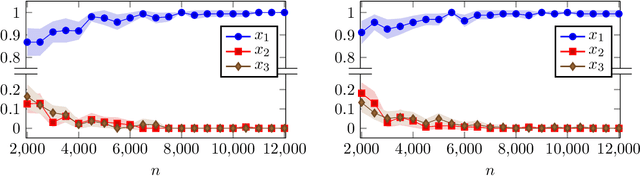
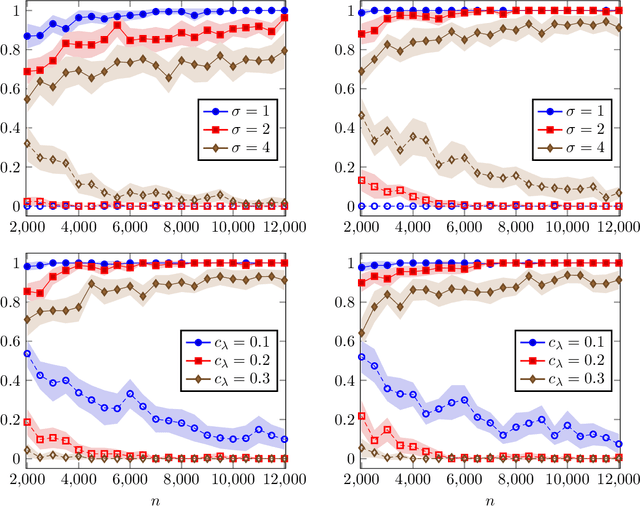
We consider a contextual online learning (multi-armed bandit) problem with high-dimensional covariate $\mathbf{x}$ and decision $\mathbf{y}$. The reward function to learn, $f(\mathbf{x},\mathbf{y})$, does not have a particular parametric form. The literature has shown that the optimal regret is $\tilde{O}(T^{(d_x+d_y+1)/(d_x+d_y+2)})$, where $d_x$ and $d_y$ are the dimensions of $\mathbf x$ and $\mathbf y$, and thus it suffers from the curse of dimensionality. In many applications, only a small subset of variables in the covariate affect the value of $f$, which is referred to as \textit{sparsity} in statistics. To take advantage of the sparsity structure of the covariate, we propose a variable selection algorithm called \textit{BV-LASSO}, which incorporates novel ideas such as binning and voting to apply LASSO to nonparametric settings. Our algorithm achieves the regret $\tilde{O}(T^{(d_x^*+d_y+1)/(d_x^*+d_y+2)})$, where $d_x^*$ is the effective covariate dimension. The regret matches the optimal regret when the covariate is $d^*_x$-dimensional and thus cannot be improved. Our algorithm may serve as a general recipe to achieve dimension reduction via variable selection in nonparametric settings.

A Dimension-free Algorithm for Contextual Continuum-armed Bandits

In contextual continuum-armed bandits, the contexts $x$ and the arms $y$ are both continuous and drawn from high-dimensional spaces. The payoff function to learn $f(x,y)$ does not have a particular parametric form. The literature has shown that for Lipschitz-continuous functions, the optimal regret is $\tilde{O}(T^{\frac{d_x+d_y+1}{d_x+d_y+2}})$, where $d_x$ and $d_y$ are the dimensions of contexts and arms, and thus suffers from the curse of dimensionality. We develop an algorithm that achieves regret $\tilde{O}(T^{\frac{d_x+1}{d_x+2}})$ when $f$ is globally concave in $y$. The global concavity is a common assumption in many applications. The algorithm is based on stochastic approximation and estimates the gradient information in an online fashion. Our results generate a valuable insight that the curse of dimensionality of the arms can be overcome with some mild structures of the payoff function.

Ranking and Selection with Covariates for Personalized Decision Making

We consider a ranking and selection problem in the context of personalized decision making, where the best alternative is not universal but varies as a function of observable covariates. The goal of ranking and selection with covariates (R&S-C) is to use sampling to compute a decision rule that can specify the best alternative with certain statistical guarantee for each subsequent individual after observing his or her covariates. A linear model is proposed to capture the relationship between the mean performance of an alternative and the covariates. Under the indifference-zone formulation, we develop two-stage procedures for both homoscedastic and heteroscedastic sampling errors, respectively, and prove their statistical validity, which is defined in terms of probability of correct selection. We also generalize the well-known slippage configuration, and prove that the generalized slippage configuration is the least favorable configuration of our procedures. Extensive numerical experiments are conducted to investigate the performance of the proposed procedures. Finally, we demonstrate the usefulness of R&S-C via a case study of selecting the best treatment regimen in the prevention of esophageal cancer. We find that by leveraging disease-related personal information, R&S-C can improve substantially the expected quality-adjusted life years for some groups of patients through providing patient-specific treatment regimen.