Sample-Optimal Large-Scale Optimal Subset Selection

Ranking and selection (R&S) conventionally aims to select the unique best alternative with the largest mean performance from a finite set of alternatives. However, for better supporting decision making, it may be more informative to deliver a small menu of alternatives whose mean performances are among the top $m$. Such problem, called optimal subset selection (OSS), is generally more challenging to address than the conventional R&S. This challenge becomes even more significant when the number of alternatives is considerably large. Thus, the focus of this paper is on addressing the large-scale OSS problem. To achieve this goal, we design a top-$m$ greedy selection mechanism that keeps sampling the current top $m$ alternatives with top $m$ running sample means and propose the explore-first top-$m$ greedy (EFG-$m$) procedure. Through an extended boundary-crossing framework, we prove that the EFG-$m$ procedure is both sample optimal and consistent in terms of the probability of good selection, confirming its effectiveness in solving large-scale OSS problem. Surprisingly, we also demonstrate that the EFG-$m$ procedure enables to achieve an indifference-based ranking within the selected subset of alternatives at no extra cost. This is highly beneficial as it delivers deeper insights to decision-makers, enabling more informed decision-makings. Lastly, numerical experiments validate our results and demonstrate the efficiency of our procedures.

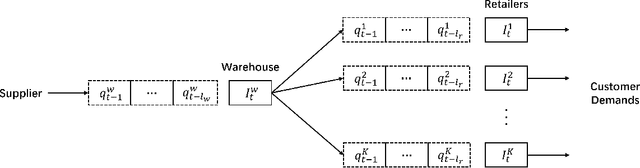
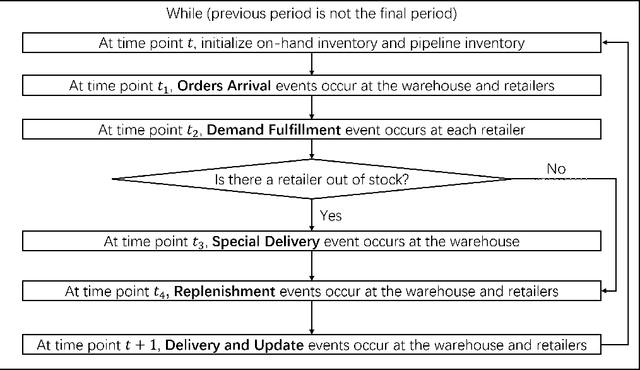
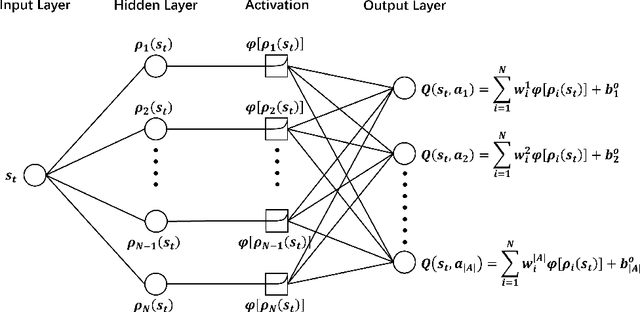
A Deep Q-Network Based on Radial Basis Functions for Multi-Echelon Inventory Management

This paper addresses a multi-echelon inventory management problem with a complex network topology where deriving optimal ordering decisions is difficult. Deep reinforcement learning (DRL) has recently shown potential in solving such problems, while designing the neural networks in DRL remains a challenge. In order to address this, a DRL model is developed whose Q-network is based on radial basis functions. The approach can be more easily constructed compared to classic DRL models based on neural networks, thus alleviating the computational burden of hyperparameter tuning. Through a series of simulation experiments, the superior performance of this approach is demonstrated compared to the simple base-stock policy, producing a better policy in the multi-echelon system and competitive performance in the serial system where the base-stock policy is optimal. In addition, the approach outperforms current DRL approaches.