Dimension Reduction in Contextual Online Learning via Nonparametric Variable Selection
Paper and Code
Sep 17, 2020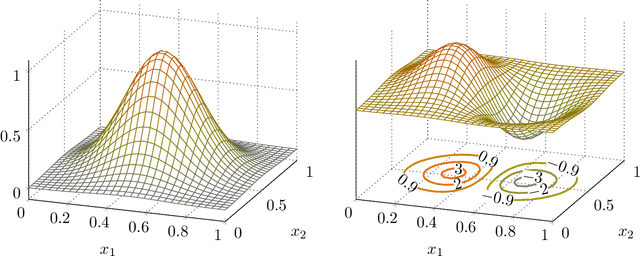
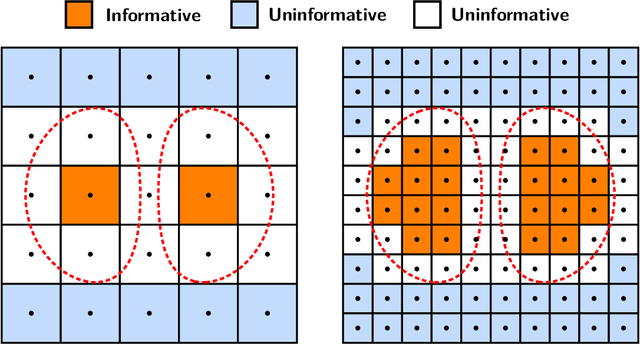
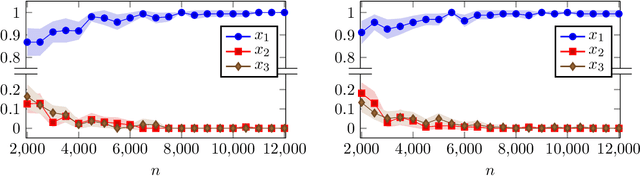
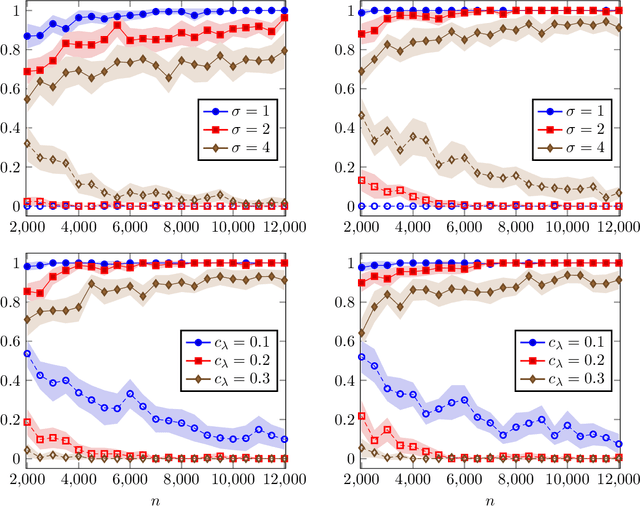
We consider a contextual online learning (multi-armed bandit) problem with high-dimensional covariate $\mathbf{x}$ and decision $\mathbf{y}$. The reward function to learn, $f(\mathbf{x},\mathbf{y})$, does not have a particular parametric form. The literature has shown that the optimal regret is $\tilde{O}(T^{(d_x+d_y+1)/(d_x+d_y+2)})$, where $d_x$ and $d_y$ are the dimensions of $\mathbf x$ and $\mathbf y$, and thus it suffers from the curse of dimensionality. In many applications, only a small subset of variables in the covariate affect the value of $f$, which is referred to as \textit{sparsity} in statistics. To take advantage of the sparsity structure of the covariate, we propose a variable selection algorithm called \textit{BV-LASSO}, which incorporates novel ideas such as binning and voting to apply LASSO to nonparametric settings. Our algorithm achieves the regret $\tilde{O}(T^{(d_x^*+d_y+1)/(d_x^*+d_y+2)})$, where $d_x^*$ is the effective covariate dimension. The regret matches the optimal regret when the covariate is $d^*_x$-dimensional and thus cannot be improved. Our algorithm may serve as a general recipe to achieve dimension reduction via variable selection in nonparametric settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge