Learning To Solve Differential Equation Constrained Optimization Problems

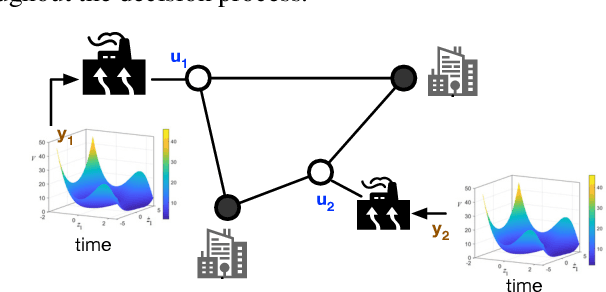
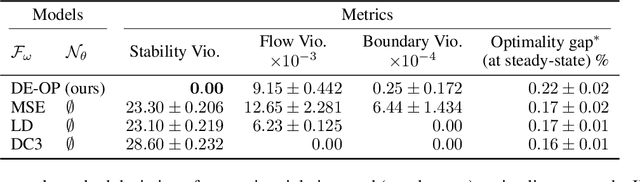
Differential equations (DE) constrained optimization plays a critical role in numerous scientific and engineering fields, including energy systems, aerospace engineering, ecology, and finance, where optimal configurations or control strategies must be determined for systems governed by ordinary or stochastic differential equations. Despite its significance, the computational challenges associated with these problems have limited their practical use. To address these limitations, this paper introduces a learning-based approach to DE-constrained optimization that combines techniques from proxy optimization and neural differential equations. The proposed approach uses a dual-network architecture, with one approximating the control strategies, focusing on steady-state constraints, and another solving the associated DEs. This combination enables the approximation of optimal strategies while accounting for dynamic constraints in near real-time. Experiments across problems in energy optimization and finance modeling show that this method provides full compliance with dynamic constraints and it produces results up to 25 times more precise than other methods which do not explicitly model the system's dynamic equations.

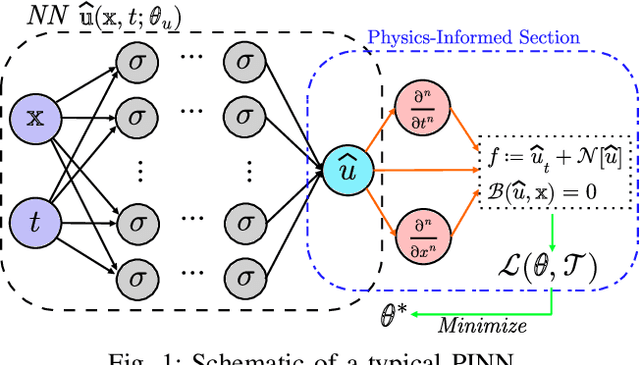
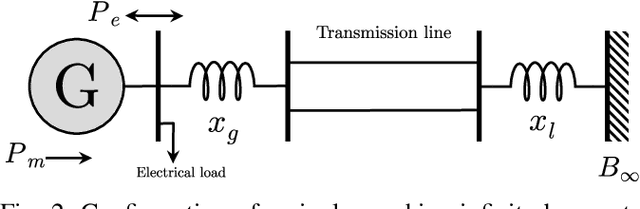
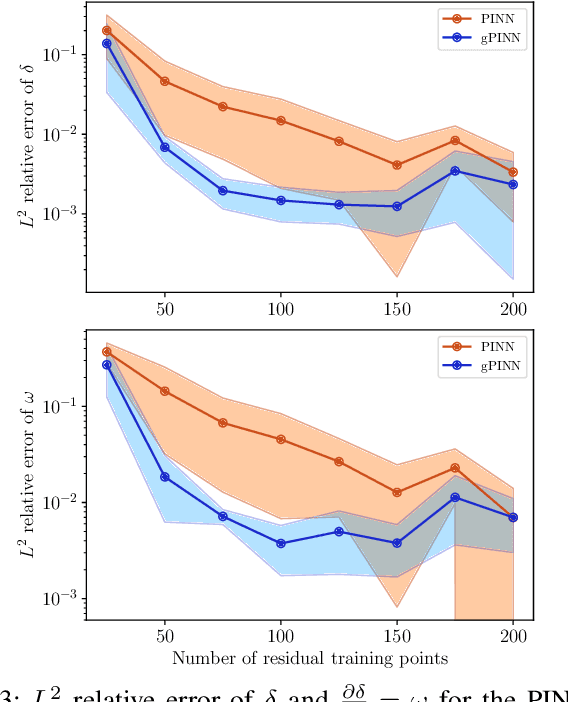
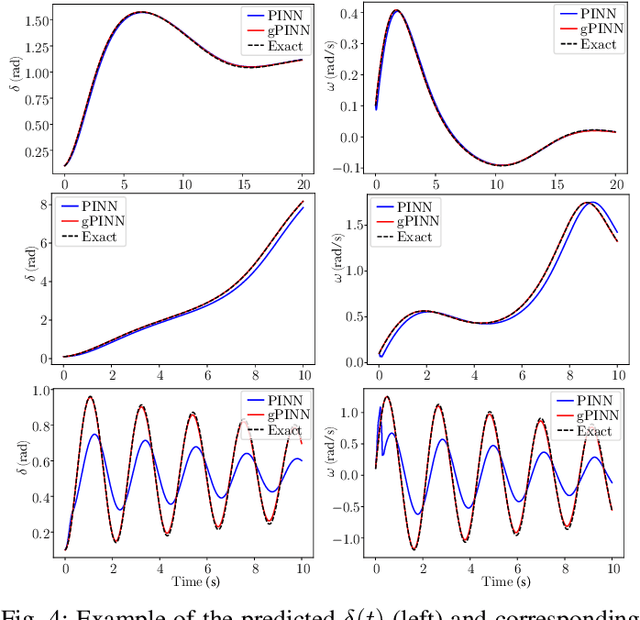
Gradient-Enhanced Physics-Informed Neural Networks for Power Systems Operational Support

The application of deep learning methods to speed up the resolution of challenging power flow problems has recently shown very encouraging results. However, power system dynamics are not snap-shot, steady-state operations. These dynamics must be considered to ensure that the optimal solutions provided by these models adhere to practical dynamical constraints, avoiding frequency fluctuations and grid instabilities. Unfortunately, dynamic system models based on ordinary or partial differential equations are frequently unsuitable for direct application in control or state estimates due to their high computational costs. To address these challenges, this paper introduces a machine learning method to approximate the behavior of power systems dynamics in near real time. The proposed framework is based on gradient-enhanced physics-informed neural networks (gPINNs) and encodes the underlying physical laws governing power systems. A key characteristic of the proposed gPINN is its ability to train without the need of generating expensive training data. The paper illustrates the potential of the proposed approach in both forward and inverse problems in a single-machine infinite bus system for predicting rotor angles and frequency, and uncertain parameters such as inertia and damping to showcase its potential for a range of power systems applications.

Towards Understanding the Unreasonable Effectiveness of Learning AC-OPF Solutions

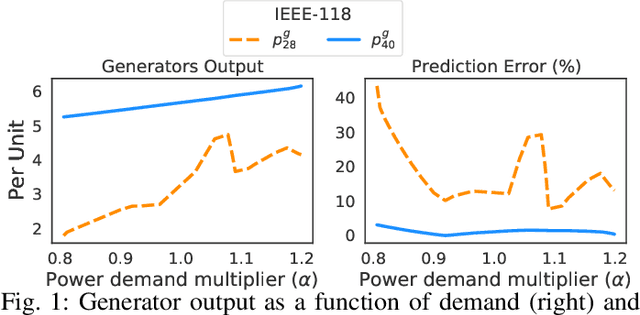
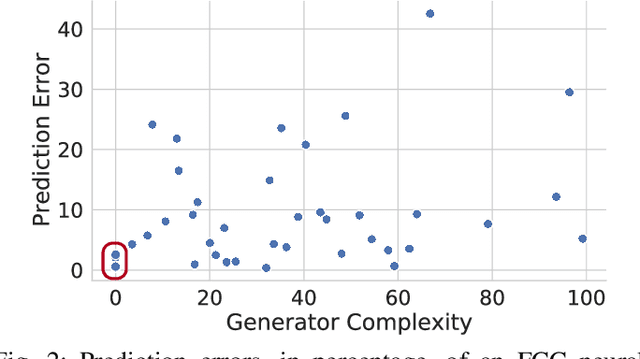
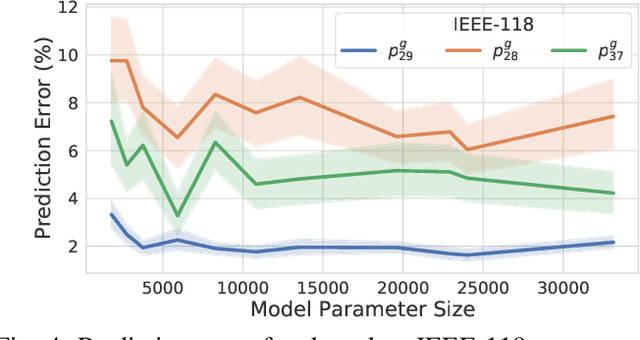
Optimal Power Flow (OPF) is a fundamental problem in power systems. It is computationally challenging and a recent line of research has proposed the use of Deep Neural Networks (DNNs) to find OPF approximations at vastly reduced runtimes when compared to those obtained by classical optimization methods. While these works show encouraging results in terms of accuracy and runtime, little is known on why these models can predict OPF solutions accurately, as well as about their robustness. This paper provides a step forward to address this knowledge gap. The paper connects the volatility of the outputs of the generators to the ability of a learning model to approximate them, it sheds light on the characteristics affecting the DNN models to learn good predictors, and it proposes a new model that exploits the observations made by this paper to produce accurate and robust OPF predictions.

OPF-Learn: An Open-Source Framework for Creating Representative AC Optimal Power Flow Datasets

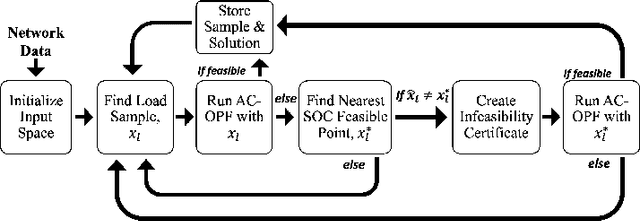
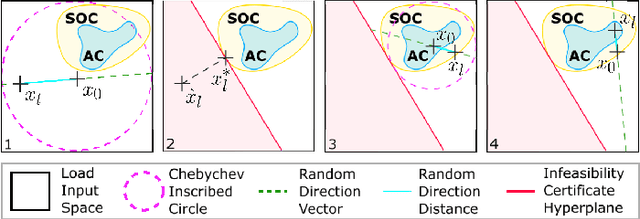
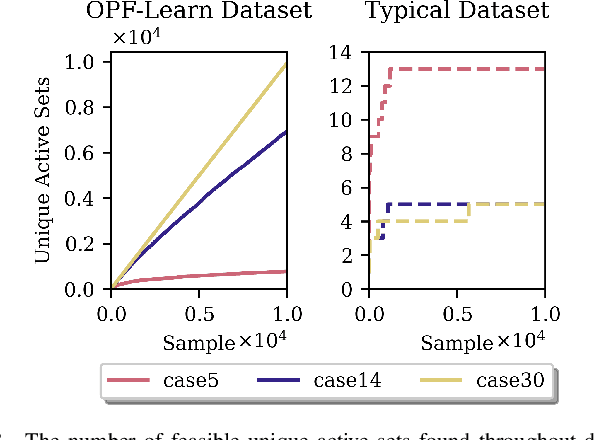
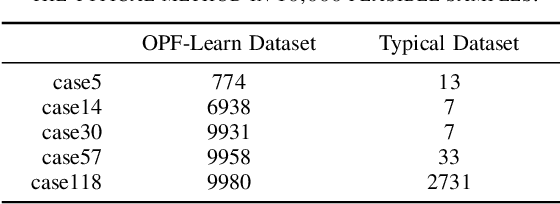
Increasing levels of renewable generation motivate a growing interest in data-driven approaches for AC optimal power flow (AC OPF) to manage uncertainty; however, a lack of disciplined dataset creation and benchmarking prohibits useful comparison among approaches in the literature. To instill confidence, models must be able to reliably predict solutions across a wide range of operating conditions. This paper develops the OPF-Learn package for Julia and Python, which uses a computationally efficient approach to create representative datasets that span a wide spectrum of the AC OPF feasible region. Load profiles are uniformly sampled from a convex set that contains the AC OPF feasible set. For each infeasible point found, the convex set is reduced using infeasibility certificates, found by using properties of a relaxed formulation. The framework is shown to generate datasets that are more representative of the entire feasible space versus traditional techniques seen in the literature, improving machine learning model performance.

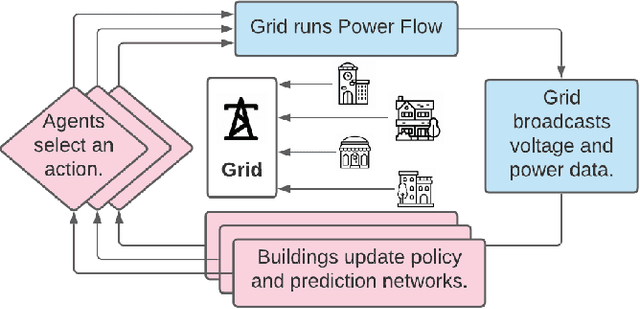
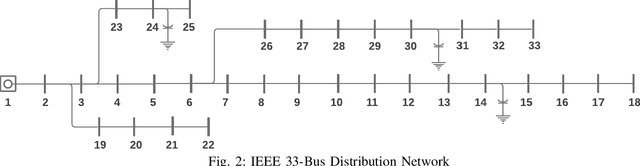
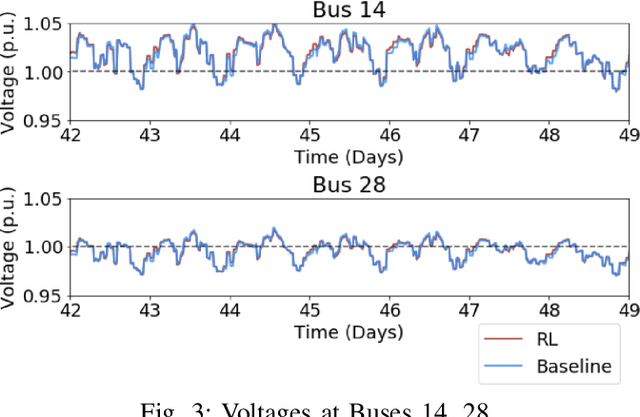
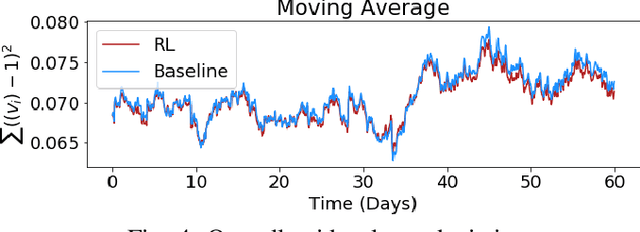
GridLearn: Multiagent Reinforcement Learning for Grid-Aware Building Energy Management

Increasing amounts of distributed generation in distribution networks can provide both challenges and opportunities for voltage regulation across the network. Intelligent control of smart inverters and other smart building energy management systems can be leveraged to alleviate these issues. GridLearn is a multiagent reinforcement learning platform that incorporates both building energy models and power flow models to achieve grid level goals, by controlling behind-the-meter resources. This study demonstrates how multi-agent reinforcement learning can preserve building owner privacy and comfort while pursuing grid-level objectives. Building upon the CityLearn framework which considers RL for building-level goals, this work expands the framework to a network setting where grid-level goals are additionally considered. As a case study, we consider voltage regulation on the IEEE-33 bus network using controllable building loads, energy storage, and smart inverters. The results show that the RL agents nominally reduce instances of undervoltages and reduce instances of overvoltages by 34%.

Enforcing Policy Feasibility Constraints through Differentiable Projection for Energy Optimization

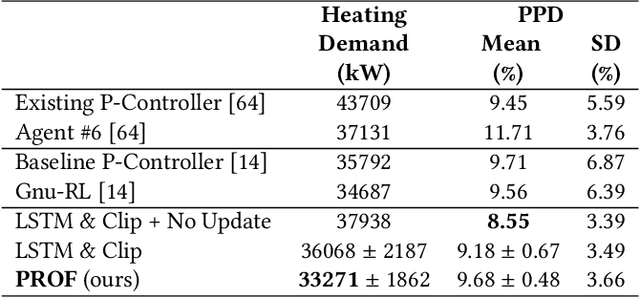
While reinforcement learning (RL) is gaining popularity in energy systems control, its real-world applications are limited due to the fact that the actions from learned policies may not satisfy functional requirements or be feasible for the underlying physical system. In this work, we propose PROjected Feasibility (PROF), a method to enforce convex operational constraints within neural policies. Specifically, we incorporate a differentiable projection layer within a neural network-based policy to enforce that all learned actions are feasible. We then update the policy end-to-end by propagating gradients through this differentiable projection layer, making the policy cognizant of the operational constraints. We demonstrate our method on two applications: energy-efficient building operation and inverter control. In the building operation setting, we show that PROF maintains thermal comfort requirements while improving energy efficiency by 4% over state-of-the-art methods. In the inverter control setting, PROF perfectly satisfies voltage constraints on the IEEE 37-bus feeder system, as it learns to curtail as little renewable energy as possible within its safety set.

Learning Optimal Solutions for Extremely Fast AC Optimal Power Flow

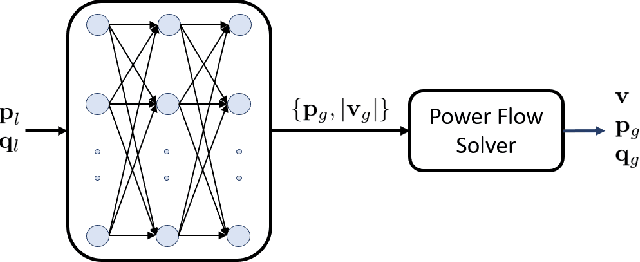
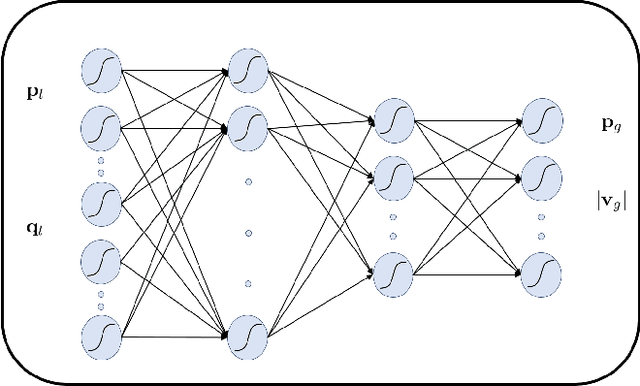
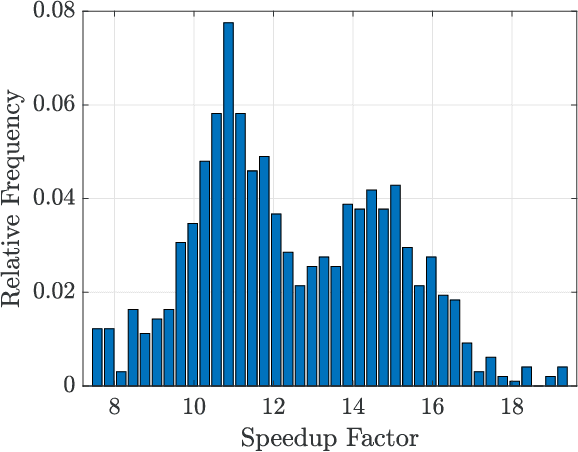
In this paper, we develop an online method that leverages machine learning to obtain feasible solutions to the AC optimal power flow (OPF) problem with negligible optimality gaps on extremely fast timescales (e.g., milliseconds), bypassing solving an AC OPF altogether. This is motivated by the fact that as the power grid experiences increasing amounts of renewable power generation, controllable loads, and other inverter-interfaced devices, faster system dynamics and quicker fluctuations in the power supply are likely to occur. Currently, grid operators typically solve AC OPF every 15 minutes to determine economic generator settings while ensuring grid constraints are satisfied. Due to the computational challenges with solving this nonconvex problem, many efforts have focused on linearizing or approximating the problem in order to solve the AC OPF on faster timescales. However, many of these approximations can be fairly poor representations of the actual system state and still require solving an optimization problem, which can be time consuming for large networks. In this work, we leverage historical data to learn a mapping between the system loading and optimal generation values, enabling us to find near-optimal and feasible AC OPF solutions on extremely fast timescales without actually solving an optimization problem.