Towards Quantifying the Carbon Emissions of Differentially Private Machine Learning

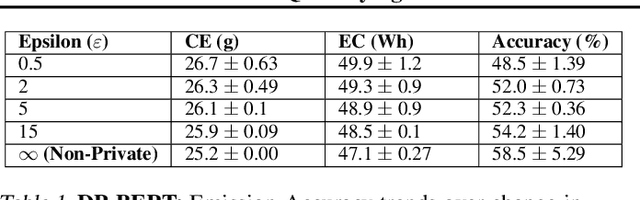
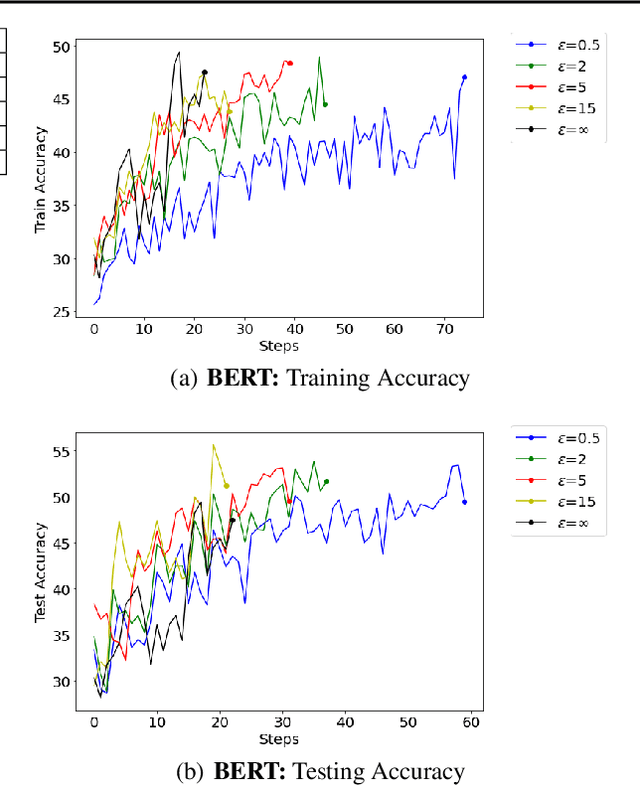
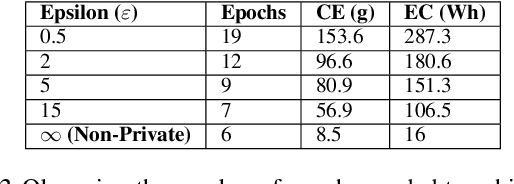
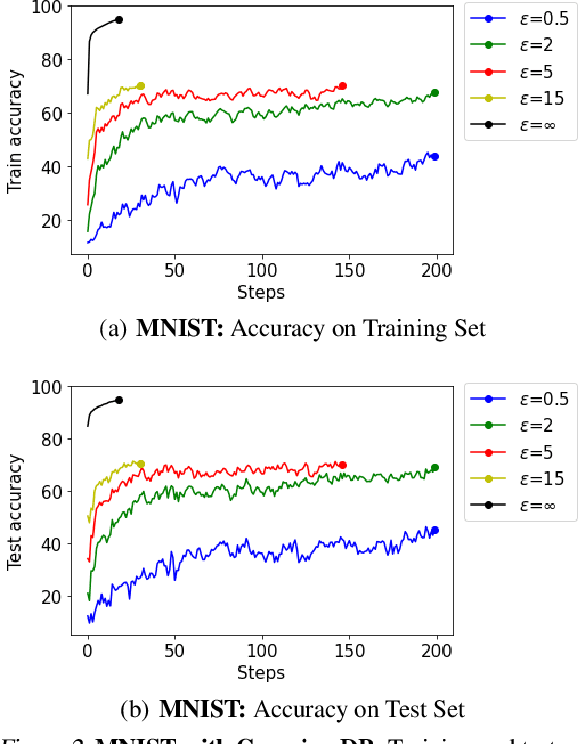
In recent years, machine learning techniques utilizing large-scale datasets have achieved remarkable performance. Differential privacy, by means of adding noise, provides strong privacy guarantees for such learning algorithms. The cost of differential privacy is often a reduced model accuracy and a lowered convergence speed. This paper investigates the impact of differential privacy on learning algorithms in terms of their carbon footprint due to either longer run-times or failed experiments. Through extensive experiments, further guidance is provided on choosing the noise levels which can strike a balance between desired privacy levels and reduced carbon emissions.

Learning Optimal Solutions for Extremely Fast AC Optimal Power Flow

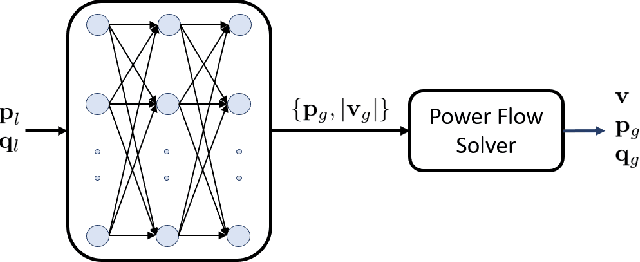
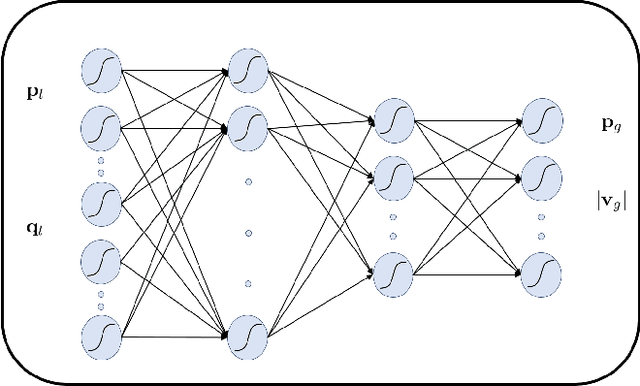
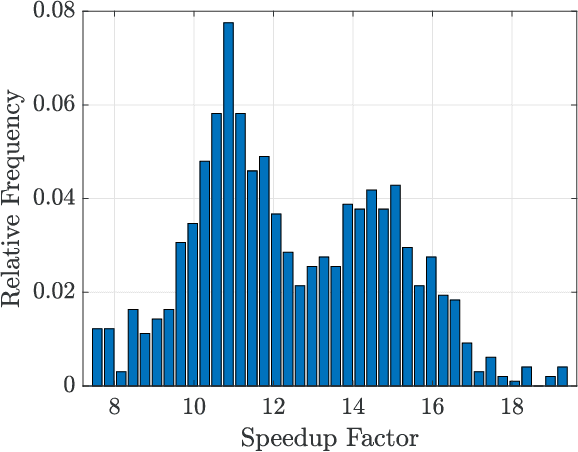
In this paper, we develop an online method that leverages machine learning to obtain feasible solutions to the AC optimal power flow (OPF) problem with negligible optimality gaps on extremely fast timescales (e.g., milliseconds), bypassing solving an AC OPF altogether. This is motivated by the fact that as the power grid experiences increasing amounts of renewable power generation, controllable loads, and other inverter-interfaced devices, faster system dynamics and quicker fluctuations in the power supply are likely to occur. Currently, grid operators typically solve AC OPF every 15 minutes to determine economic generator settings while ensuring grid constraints are satisfied. Due to the computational challenges with solving this nonconvex problem, many efforts have focused on linearizing or approximating the problem in order to solve the AC OPF on faster timescales. However, many of these approximations can be fairly poor representations of the actual system state and still require solving an optimization problem, which can be time consuming for large networks. In this work, we leverage historical data to learn a mapping between the system loading and optimal generation values, enabling us to find near-optimal and feasible AC OPF solutions on extremely fast timescales without actually solving an optimization problem.