Learning To Solve Differential Equation Constrained Optimization Problems

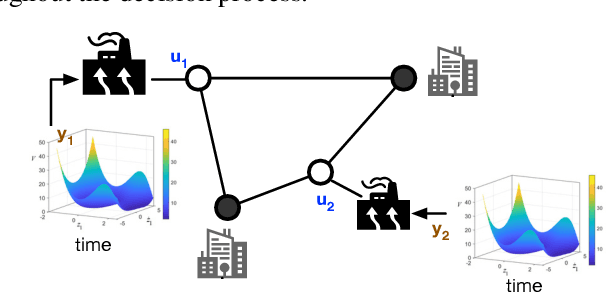
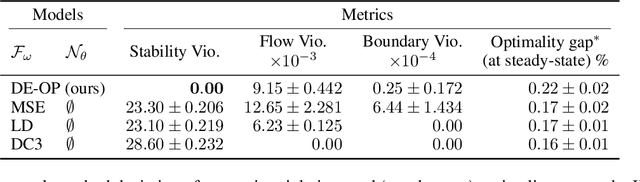
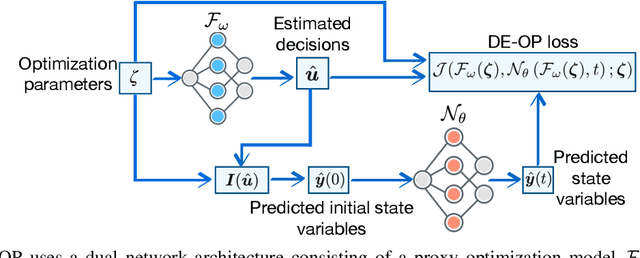
Differential equations (DE) constrained optimization plays a critical role in numerous scientific and engineering fields, including energy systems, aerospace engineering, ecology, and finance, where optimal configurations or control strategies must be determined for systems governed by ordinary or stochastic differential equations. Despite its significance, the computational challenges associated with these problems have limited their practical use. To address these limitations, this paper introduces a learning-based approach to DE-constrained optimization that combines techniques from proxy optimization and neural differential equations. The proposed approach uses a dual-network architecture, with one approximating the control strategies, focusing on steady-state constraints, and another solving the associated DEs. This combination enables the approximation of optimal strategies while accounting for dynamic constraints in near real-time. Experiments across problems in energy optimization and finance modeling show that this method provides full compliance with dynamic constraints and it produces results up to 25 times more precise than other methods which do not explicitly model the system's dynamic equations.

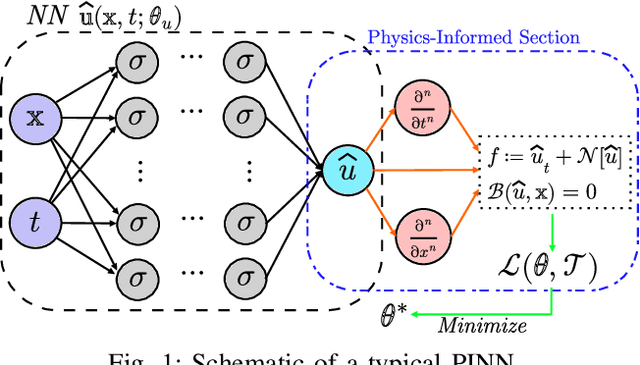
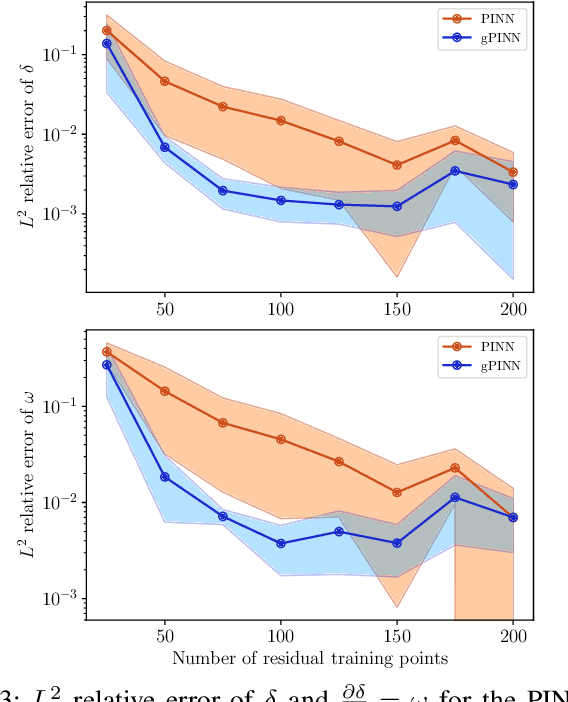
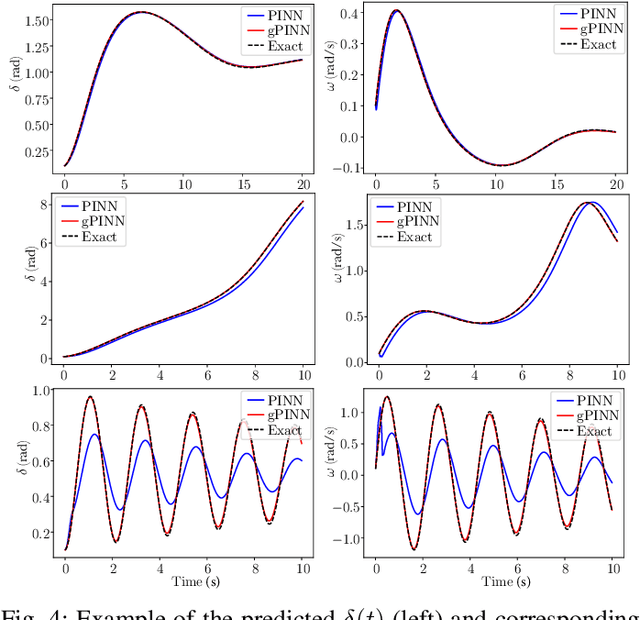
Gradient-Enhanced Physics-Informed Neural Networks for Power Systems Operational Support

The application of deep learning methods to speed up the resolution of challenging power flow problems has recently shown very encouraging results. However, power system dynamics are not snap-shot, steady-state operations. These dynamics must be considered to ensure that the optimal solutions provided by these models adhere to practical dynamical constraints, avoiding frequency fluctuations and grid instabilities. Unfortunately, dynamic system models based on ordinary or partial differential equations are frequently unsuitable for direct application in control or state estimates due to their high computational costs. To address these challenges, this paper introduces a machine learning method to approximate the behavior of power systems dynamics in near real time. The proposed framework is based on gradient-enhanced physics-informed neural networks (gPINNs) and encodes the underlying physical laws governing power systems. A key characteristic of the proposed gPINN is its ability to train without the need of generating expensive training data. The paper illustrates the potential of the proposed approach in both forward and inverse problems in a single-machine infinite bus system for predicting rotor angles and frequency, and uncertain parameters such as inertia and damping to showcase its potential for a range of power systems applications.

Towards Understanding the Unreasonable Effectiveness of Learning AC-OPF Solutions

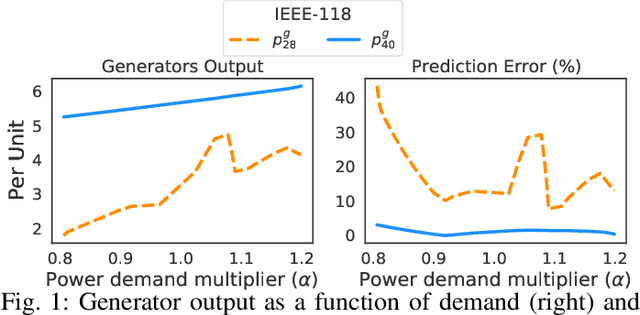
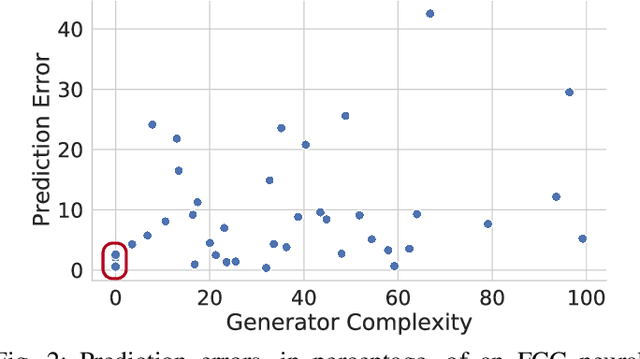
Optimal Power Flow (OPF) is a fundamental problem in power systems. It is computationally challenging and a recent line of research has proposed the use of Deep Neural Networks (DNNs) to find OPF approximations at vastly reduced runtimes when compared to those obtained by classical optimization methods. While these works show encouraging results in terms of accuracy and runtime, little is known on why these models can predict OPF solutions accurately, as well as about their robustness. This paper provides a step forward to address this knowledge gap. The paper connects the volatility of the outputs of the generators to the ability of a learning model to approximate them, it sheds light on the characteristics affecting the DNN models to learn good predictors, and it proposes a new model that exploits the observations made by this paper to produce accurate and robust OPF predictions.