Learning To Solve Differential Equation Constrained Optimization Problems
Paper and Code
Oct 02, 2024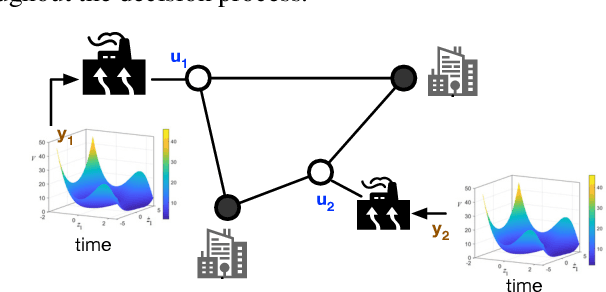
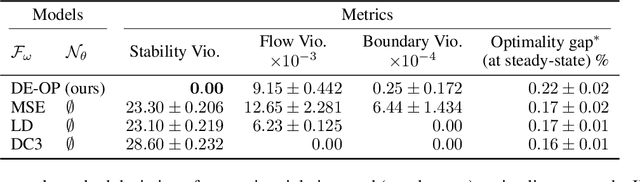


Differential equations (DE) constrained optimization plays a critical role in numerous scientific and engineering fields, including energy systems, aerospace engineering, ecology, and finance, where optimal configurations or control strategies must be determined for systems governed by ordinary or stochastic differential equations. Despite its significance, the computational challenges associated with these problems have limited their practical use. To address these limitations, this paper introduces a learning-based approach to DE-constrained optimization that combines techniques from proxy optimization and neural differential equations. The proposed approach uses a dual-network architecture, with one approximating the control strategies, focusing on steady-state constraints, and another solving the associated DEs. This combination enables the approximation of optimal strategies while accounting for dynamic constraints in near real-time. Experiments across problems in energy optimization and finance modeling show that this method provides full compliance with dynamic constraints and it produces results up to 25 times more precise than other methods which do not explicitly model the system's dynamic equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge