Learning Fair Ranking Policies via Differentiable Optimization of Ordered Weighted Averages

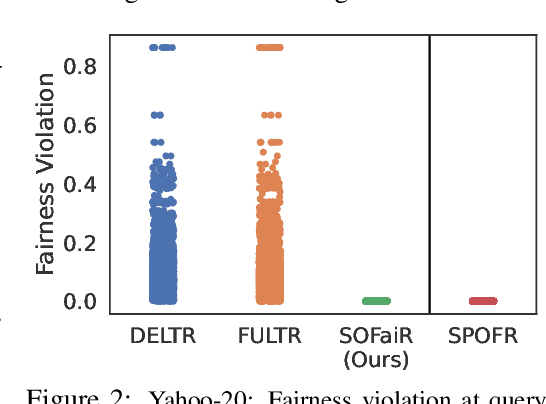
Learning to Rank (LTR) is one of the most widely used machine learning applications. It is a key component in platforms with profound societal impacts, including job search, healthcare information retrieval, and social media content feeds. Conventional LTR models have been shown to produce biases results, stimulating a discourse on how to address the disparities introduced by ranking systems that solely prioritize user relevance. However, while several models of fair learning to rank have been proposed, they suffer from deficiencies either in accuracy or efficiency, thus limiting their applicability to real-world ranking platforms. This paper shows how efficiently-solvable fair ranking models, based on the optimization of Ordered Weighted Average (OWA) functions, can be integrated into the training loop of an LTR model to achieve favorable balances between fairness, user utility, and runtime efficiency. In particular, this paper is the first to show how to backpropagate through constrained optimizations of OWA objectives, enabling their use in integrated prediction and decision models.

Folded Optimization for End-to-End Model-Based Learning

The integration of constrained optimization models as components in deep networks has led to promising advances in both these domains. A primary challenge in this setting is backpropagation through the optimization mapping, which typically lacks a closed form. A common approach is unrolling, which relies on automatic differentiation through the operations of an iterative solver. While flexible and general, unrolling can encounter accuracy and efficiency issues in practice. These issues can be avoided by differentiating the optimization mapping analytically, but current frameworks impose rigid requirements on the optimization problem's form. This paper provides theoretical insights into the backpropagation of unrolled optimizers, which lead to a system for generating equivalent but efficiently solvable analytical models. Additionally, it proposes a unifying view of unrolling and analytical differentiation through constrained optimization mappings. Experiments over various structured prediction and decision-focused learning tasks illustrate the potential of the approach both computationally and in terms of enhanced expressiveness.

Context-Aware Differential Privacy for Language Modeling

The remarkable ability of language models (LMs) has also brought challenges at the interface of AI and security. A critical challenge pertains to how much information these models retain and leak about the training data. This is particularly urgent as the typical development of LMs relies on huge, often highly sensitive data, such as emails and chat logs. To contrast this shortcoming, this paper introduces Context-Aware Differentially Private Language Model (CADP-LM) , a privacy-preserving LM framework that relies on two key insights: First, it utilizes the notion of \emph{context} to define and audit the potentially sensitive information. Second, it adopts the notion of Differential Privacy to protect sensitive information and characterize the privacy leakage. A unique characteristic of CADP-LM is its ability to target the protection of sensitive sentences and contexts only, providing a highly accurate private model. Experiments on a variety of datasets and settings demonstrate these strengths of CADP-LM.

Towards Understanding the Unreasonable Effectiveness of Learning AC-OPF Solutions

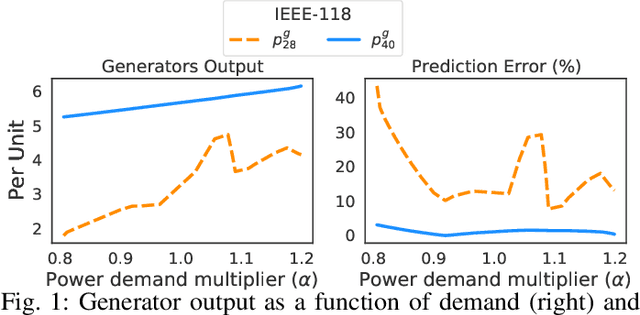
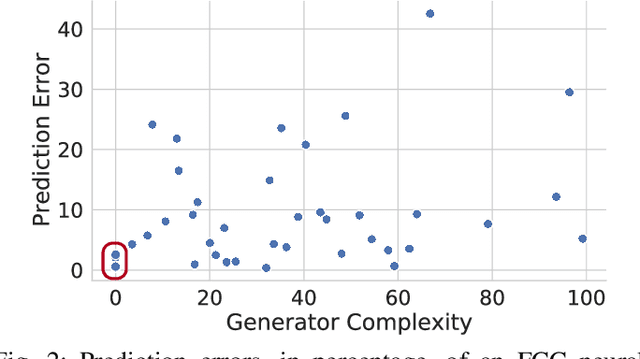
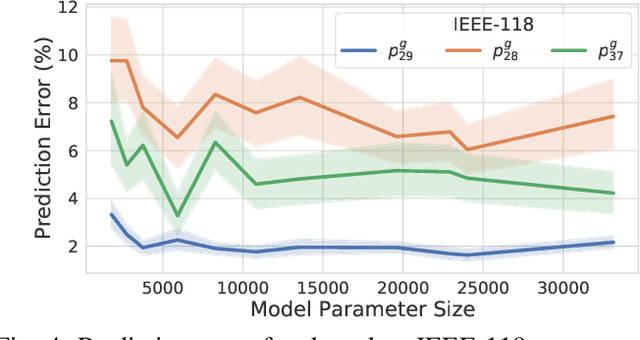
Optimal Power Flow (OPF) is a fundamental problem in power systems. It is computationally challenging and a recent line of research has proposed the use of Deep Neural Networks (DNNs) to find OPF approximations at vastly reduced runtimes when compared to those obtained by classical optimization methods. While these works show encouraging results in terms of accuracy and runtime, little is known on why these models can predict OPF solutions accurately, as well as about their robustness. This paper provides a step forward to address this knowledge gap. The paper connects the volatility of the outputs of the generators to the ability of a learning model to approximate them, it sheds light on the characteristics affecting the DNN models to learn good predictors, and it proposes a new model that exploits the observations made by this paper to produce accurate and robust OPF predictions.

A Fairness Analysis on Private Aggregation of Teacher Ensembles

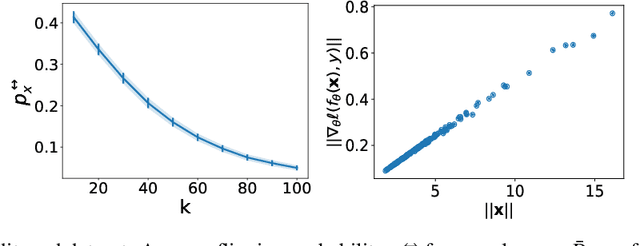
The Private Aggregation of Teacher Ensembles (PATE) is an important private machine learning framework. It combines multiple learning models used as teachers for a student model that learns to predict an output chosen by noisy voting among the teachers. The resulting model satisfies differential privacy and has been shown effective in learning high-quality private models in semisupervised settings or when one wishes to protect the data labels. This paper asks whether this privacy-preserving framework introduces or exacerbates bias and unfairness and shows that PATE can introduce accuracy disparity among individuals and groups of individuals. The paper analyzes which algorithmic and data properties are responsible for the disproportionate impacts, why these aspects are affecting different groups disproportionately, and proposes guidelines to mitigate these effects. The proposed approach is evaluated on several datasets and settings.

Differentially Private Deep Learning under the Fairness Lens

Differential Privacy (DP) is an important privacy-enhancing technology for private machine learning systems. It allows to measure and bound the risk associated with an individual participation in a computation. However, it was recently observed that DP learning systems may exacerbate bias and unfairness for different groups of individuals. This paper builds on these important observations and sheds light on the causes of the disparate impacts arising in the problem of differentially private empirical risk minimization. It focuses on the accuracy disparity arising among groups of individuals in two well-studied DP learning methods: output perturbation and differentially private stochastic gradient descent. The paper analyzes which data and model properties are responsible for the disproportionate impacts, why these aspects are affecting different groups disproportionately and proposes guidelines to mitigate these effects. The proposed approach is evaluated on several datasets and settings.