Gradient-Enhanced Physics-Informed Neural Networks for Power Systems Operational Support
Paper and Code
Jun 21, 2022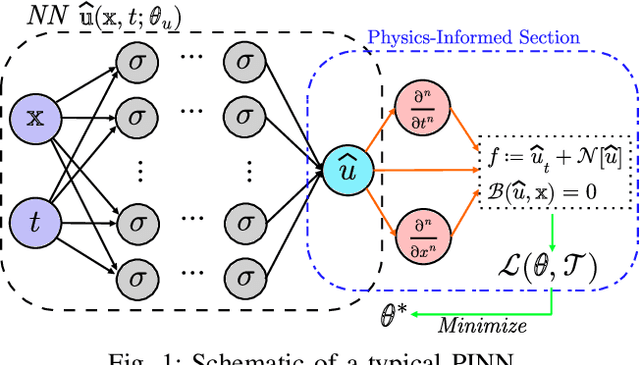
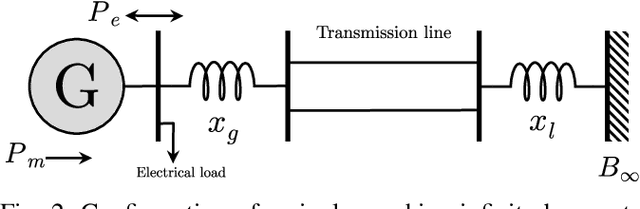
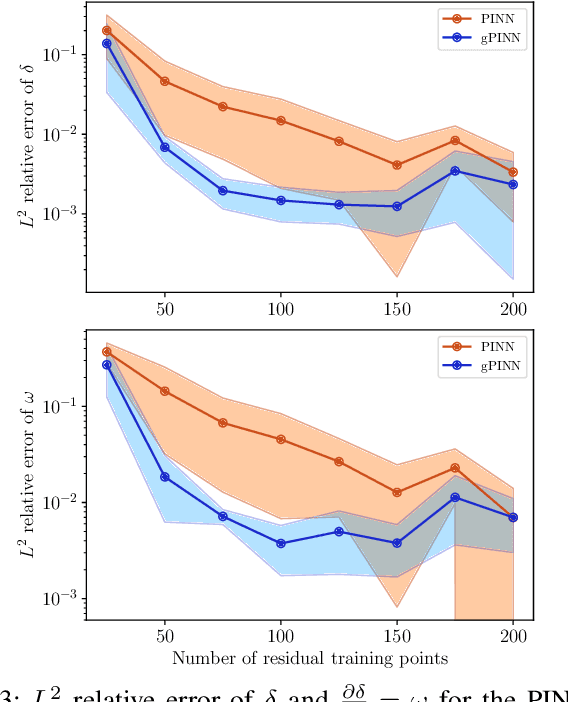
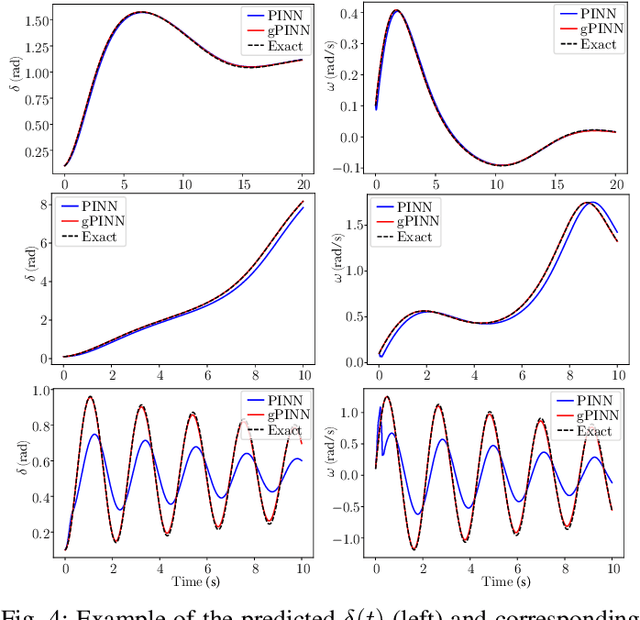
The application of deep learning methods to speed up the resolution of challenging power flow problems has recently shown very encouraging results. However, power system dynamics are not snap-shot, steady-state operations. These dynamics must be considered to ensure that the optimal solutions provided by these models adhere to practical dynamical constraints, avoiding frequency fluctuations and grid instabilities. Unfortunately, dynamic system models based on ordinary or partial differential equations are frequently unsuitable for direct application in control or state estimates due to their high computational costs. To address these challenges, this paper introduces a machine learning method to approximate the behavior of power systems dynamics in near real time. The proposed framework is based on gradient-enhanced physics-informed neural networks (gPINNs) and encodes the underlying physical laws governing power systems. A key characteristic of the proposed gPINN is its ability to train without the need of generating expensive training data. The paper illustrates the potential of the proposed approach in both forward and inverse problems in a single-machine infinite bus system for predicting rotor angles and frequency, and uncertain parameters such as inertia and damping to showcase its potential for a range of power systems applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge