Collision Induced Binding and Transport of Shape Changing Robot Pairs

We report in experiment and simulation the spontaneous formation of dynamically bound pairs of shape changing robots undergoing locally repulsive collisions. These physical `gliders' robustly emerge from an ensemble of individually undulating three-link two-motor robots and can remain bound for hundreds of undulations and travel for multiple robot dimensions. Gliders occur in two distinct binding symmetries and form over a wide range of angular oscillation extent. This parameter sets the maximal concavity which influences formation probability and translation characteristics. Analysis of dynamics in simulation reveals the mechanism of effective dynamical attraction -- a result of the emergent interplay of appropriately oriented and timed repulsive interactions. Tactile sensing stabilizes the short-lived conformation via concavity modulation.

Low rattling: A predictive principle for self-organization in active collectives

Self-organization is frequently observed in active collectives, from ant rafts to molecular motor assemblies. General principles describing self-organization away from equilibrium have been challenging to identify. We offer a unifying framework that models the behavior of complex systems as largely random, while capturing their configuration-dependent response to external forcing. This allows derivation of a Boltzmann-like principle for understanding and manipulating driven self-organization. We validate our predictions experimentally in shape-changing robotic active matter, and outline a methodology for controlling collective behavior. Our findings highlight how emergent order depends sensitively on the matching between external patterns of forcing and internal dynamical response properties, pointing towards future approaches for design and control of active particle mixtures and metamaterials.

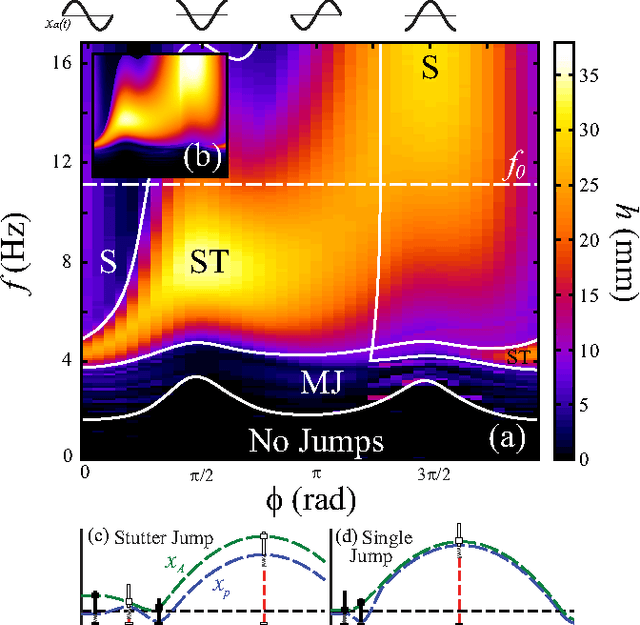
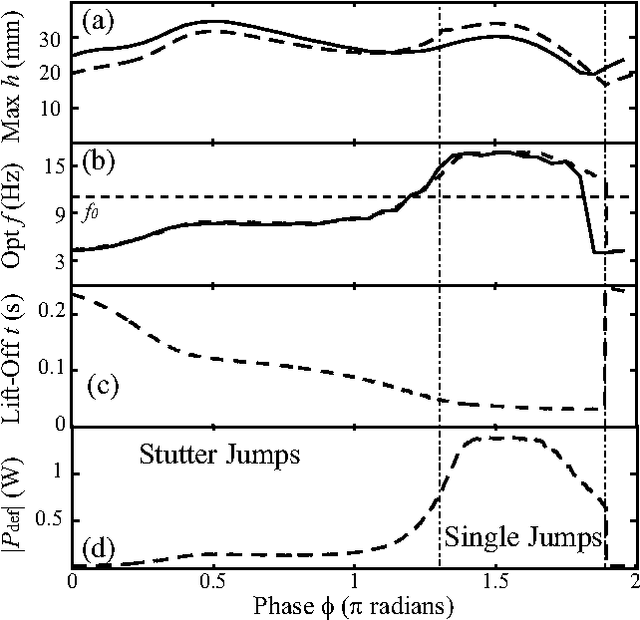
Lift-off dynamics in a simple jumping robot

We study vertical jumping in a simple robot comprising an actuated mass-spring arrangement. The actuator frequency and phase are systematically varied to find optimal performance. Optimal jumps occur above and below (but not at) the robot's resonant frequency $f_0$. Two distinct jumping modes emerge: a simple jump which is optimal above $f_0$ is achievable with a squat maneuver, and a peculiar stutter jump which is optimal below $f_0$ is generated with a counter-movement. A simple dynamical model reveals how optimal lift-off results from non-resonant transient dynamics.