A review on locomotion robophysics: the study of movement at the intersection of robotics, soft matter and dynamical systems

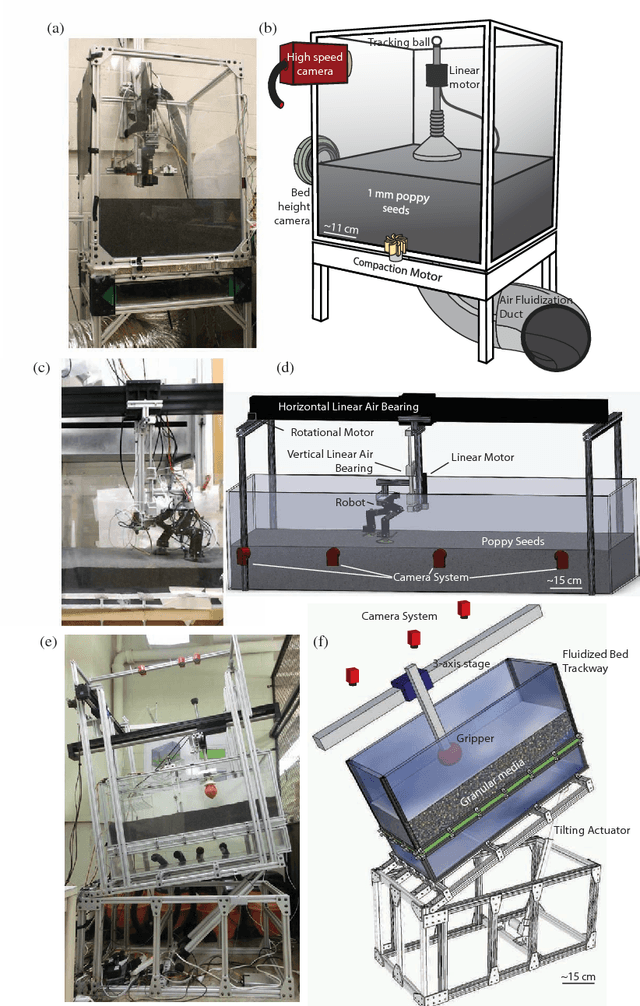
In this review we argue for the creation of a physics of moving systems -- a locomotion "robophysics" -- which we define as the pursuit of the discovery of principles of self generated motion. Robophysics can provide an important intellectual complement to the discipline of robotics, largely the domain of researchers from engineering and computer science. The essential idea is that we must complement study of complex robots in complex situations with systematic study of simplified robophysical devices in controlled laboratory settings and simplified theoretical models. We must thus use the methods of physics to examine successful and failed locomotion in simplified (abstracted) devices using parameter space exploration, systematic control, and techniques from dynamical systems. Using examples from our and other's research, we will discuss how such robophysical studies have begun to aid engineers in the creation of devices that begin to achieve life-like locomotor abilities on and within complex environments, have inspired interesting physics questions in low dimensional dynamical systems, geometric mechanics and soft matter physics, and have been useful to develop models for biological locomotion in complex terrain. The rapidly decreasing cost of constructing sophisticated robot models with easy access to significant computational power bodes well for scientists and engineers to engage in a discipline which can readily integrate experiment, theory and computation.

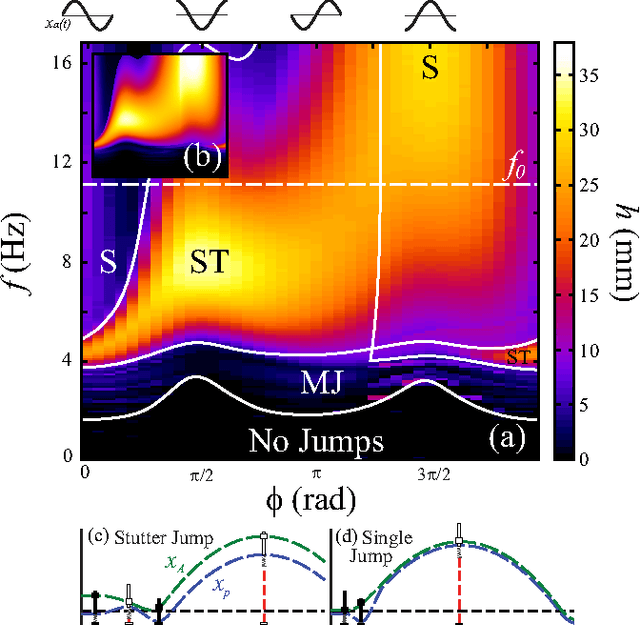
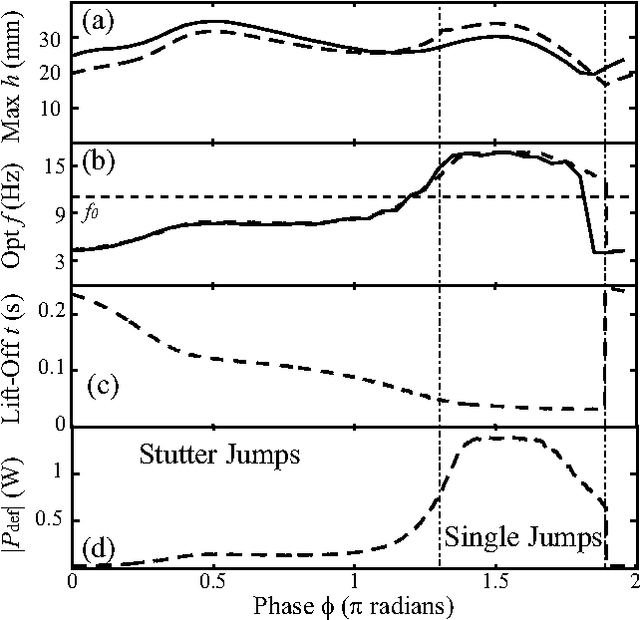
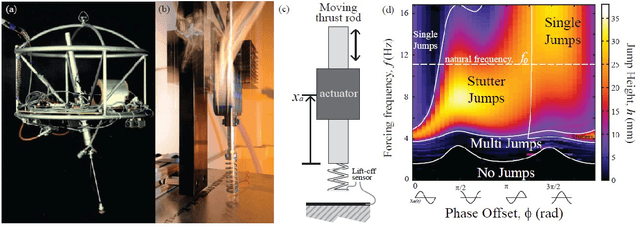
Lift-off dynamics in a simple jumping robot

We study vertical jumping in a simple robot comprising an actuated mass-spring arrangement. The actuator frequency and phase are systematically varied to find optimal performance. Optimal jumps occur above and below (but not at) the robot's resonant frequency $f_0$. Two distinct jumping modes emerge: a simple jump which is optimal above $f_0$ is achievable with a squat maneuver, and a peculiar stutter jump which is optimal below $f_0$ is generated with a counter-movement. A simple dynamical model reveals how optimal lift-off results from non-resonant transient dynamics.