Lift-off dynamics in a simple jumping robot
Paper and Code
Aug 30, 2012
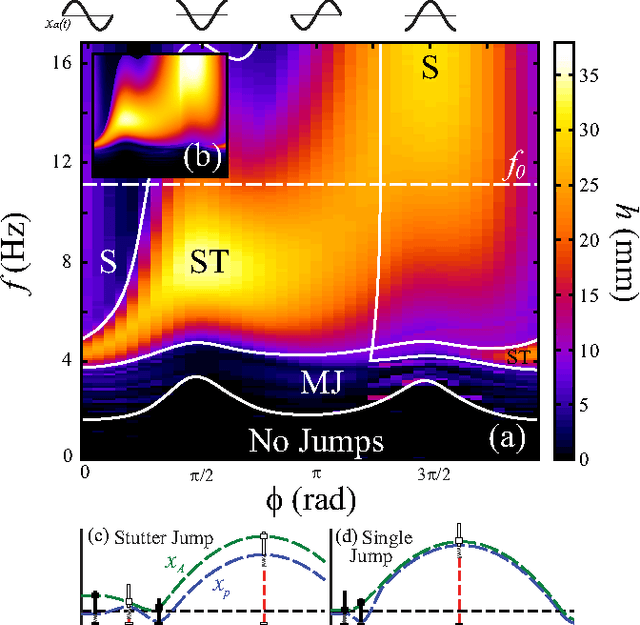
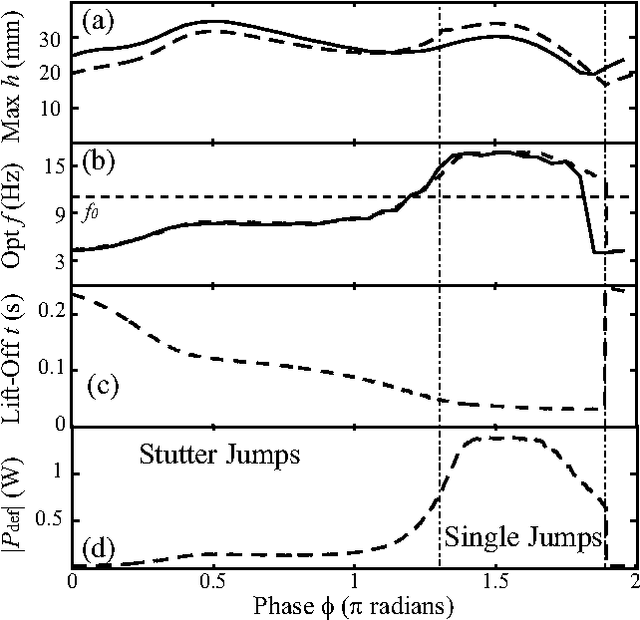

We study vertical jumping in a simple robot comprising an actuated mass-spring arrangement. The actuator frequency and phase are systematically varied to find optimal performance. Optimal jumps occur above and below (but not at) the robot's resonant frequency $f_0$. Two distinct jumping modes emerge: a simple jump which is optimal above $f_0$ is achievable with a squat maneuver, and a peculiar stutter jump which is optimal below $f_0$ is generated with a counter-movement. A simple dynamical model reveals how optimal lift-off results from non-resonant transient dynamics.
* 4 pages, 4 figures, Physical Review Letters, in press (2012)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge