Precise characterization of the prior predictive distribution of deep ReLU networks

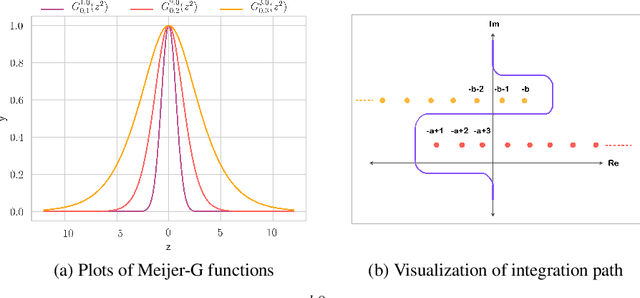
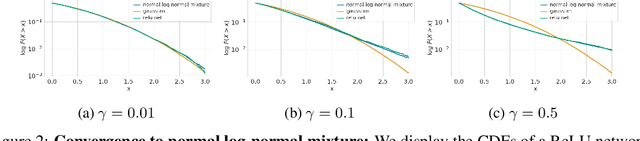
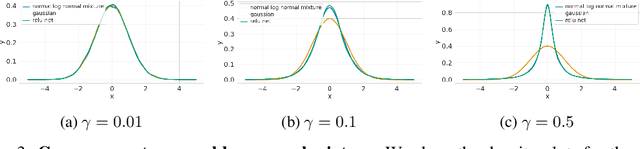
Recent works on Bayesian neural networks (BNNs) have highlighted the need to better understand the implications of using Gaussian priors in combination with the compositional structure of the network architecture. Similar in spirit to the kind of analysis that has been developed to devise better initialization schemes for neural networks (cf. He- or Xavier initialization), we derive a precise characterization of the prior predictive distribution of finite-width ReLU networks with Gaussian weights. While theoretical results have been obtained for their heavy-tailedness, the full characterization of the prior predictive distribution (i.e. its density, CDF and moments), remained unknown prior to this work. Our analysis, based on the Meijer-G function, allows us to quantify the influence of architectural choices such as the width or depth of the network on the resulting shape of the prior predictive distribution. We also formally connect our results to previous work in the infinite width setting, demonstrating that the moments of the distribution converge to those of a normal log-normal mixture in the infinite depth limit. Finally, our results provide valuable guidance on prior design: for instance, controlling the predictive variance with depth- and width-informed priors on the weights of the network.

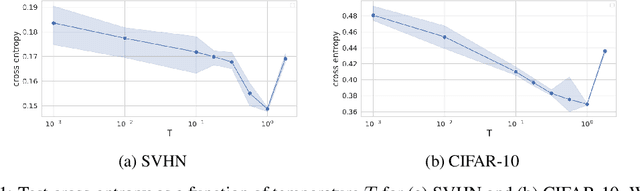
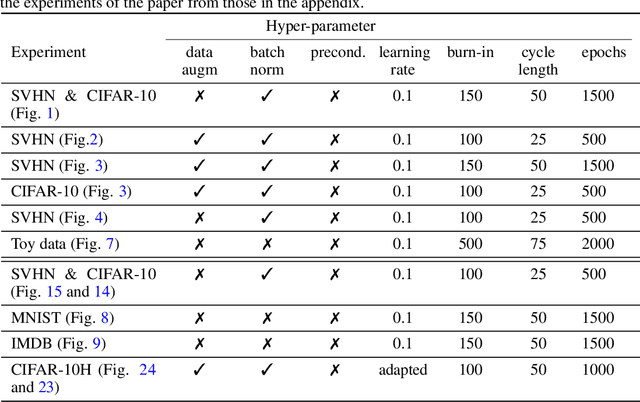
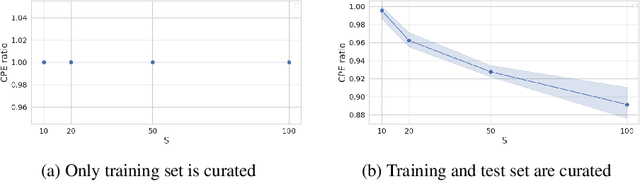
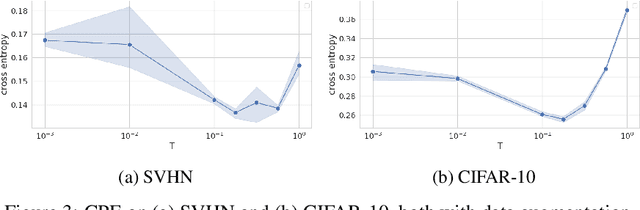
Disentangling the Roles of Curation, Data-Augmentation and the Prior in the Cold Posterior Effect

The "cold posterior effect" (CPE) in Bayesian deep learning describes the uncomforting observation that the predictive performance of Bayesian neural networks can be significantly improved if the Bayes posterior is artificially sharpened using a temperature parameter T<1. The CPE is problematic in theory and practice and since the effect was identified many researchers have proposed hypotheses to explain the phenomenon. However, despite this intensive research effort the effect remains poorly understood. In this work we provide novel and nuanced evidence relevant to existing explanations for the cold posterior effect, disentangling three hypotheses: 1. The dataset curation hypothesis of Aitchison (2020): we show empirically that the CPE does not arise in a real curated data set but can be produced in a controlled experiment with varying curation strength. 2. The data augmentation hypothesis of Izmailov et al. (2021) and Fortuin et al. (2021): we show empirically that data augmentation is sufficient but not necessary for the CPE to be present. 3. The bad prior hypothesis of Wenzel et al. (2020): we use a simple experiment evaluating the relative importance of the prior and the likelihood, strongly linking the CPE to the prior. Our results demonstrate how the CPE can arise in isolation from synthetic curation, data augmentation, and bad priors. Cold posteriors observed "in the wild" are therefore unlikely to arise from a single simple cause; as a result, we do not expect a simple "fix" for cold posteriors.

A Primer on Multi-Neuron Relaxation-based Adversarial Robustness Certification

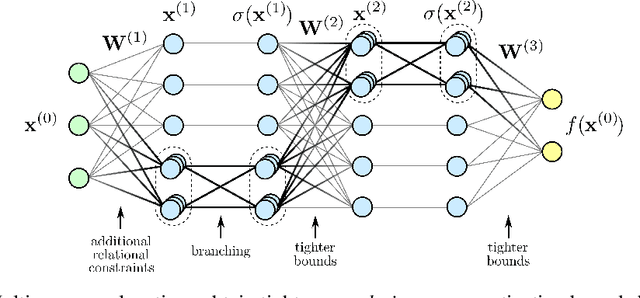
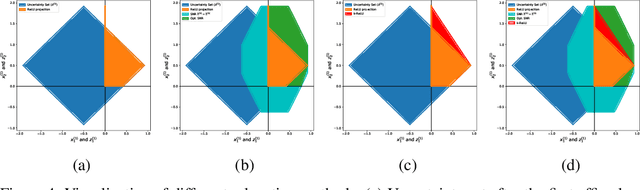
The existence of adversarial examples poses a real danger when deep neural networks are deployed in the real world. The go-to strategy to quantify this vulnerability is to evaluate the model against specific attack algorithms. This approach is however inherently limited, as it says little about the robustness of the model against more powerful attacks not included in the evaluation. We develop a unified mathematical framework to describe relaxation-based robustness certification methods, which go beyond adversary-specific robustness evaluation and instead provide provable robustness guarantees against attacks by any adversary. We discuss the fundamental limitations posed by single-neuron relaxations and show how the recent ``k-ReLU'' multi-neuron relaxation framework of Singh et al. (2019) obtains tighter correlation-aware activation bounds by leveraging additional relational constraints among groups of neurons. Specifically, we show how additional pre-activation bounds can be mapped to corresponding post-activation bounds and how they can in turn be used to obtain tighter robustness certificates. We also present an intuitive way to visualize different relaxation-based certification methods. By approximating multiple non-linearities jointly instead of separately, the k-ReLU method is able to bypass the convex barrier imposed by single neuron relaxations.

The k-tied Normal Distribution: A Compact Parameterization of Gaussian Mean Field Posteriors in Bayesian Neural Networks

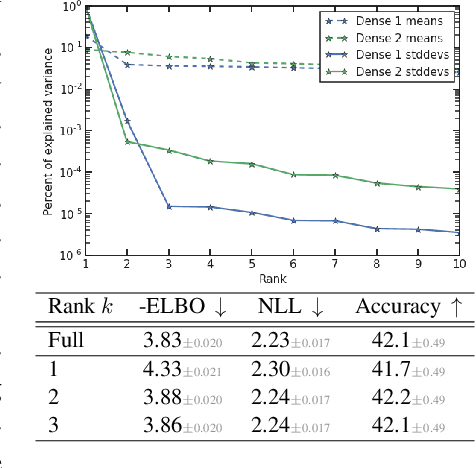
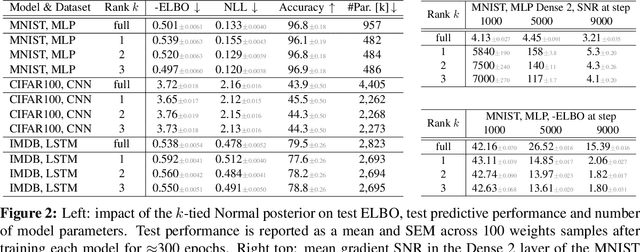
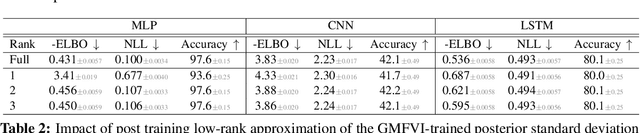
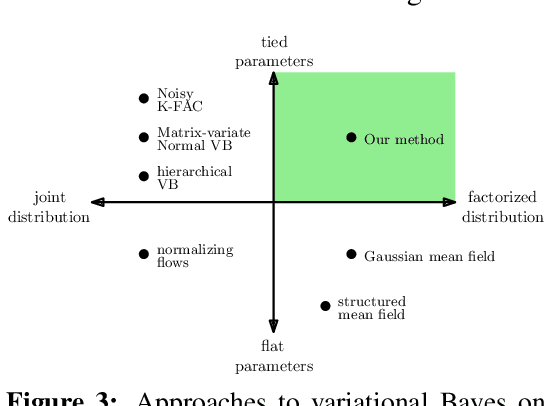
Variational Bayesian Inference is a popular methodology for approximating posterior distributions over Bayesian neural network weights. Recent work developing this class of methods has explored ever richer parameterizations of the approximate posterior in the hope of improving performance. In contrast, here we share a curious experimental finding that suggests instead restricting the variational distribution to a more compact parameterization. For a variety of deep Bayesian neural networks trained using Gaussian mean-field variational inference, we find that the posterior standard deviations consistently exhibit strong low-rank structure after convergence. This means that by decomposing these variational parameters into a low-rank factorization, we can make our variational approximation more compact without decreasing the models' performance. Furthermore, we find that such factorized parameterizations improve the signal-to-noise ratio of stochastic gradient estimates of the variational lower bound, resulting in faster convergence.

How Good is the Bayes Posterior in Deep Neural Networks Really?

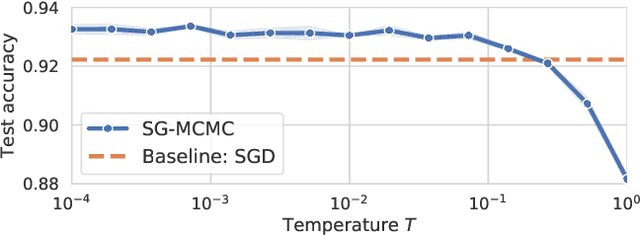
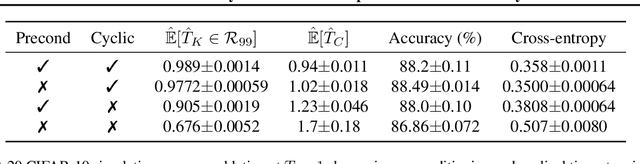
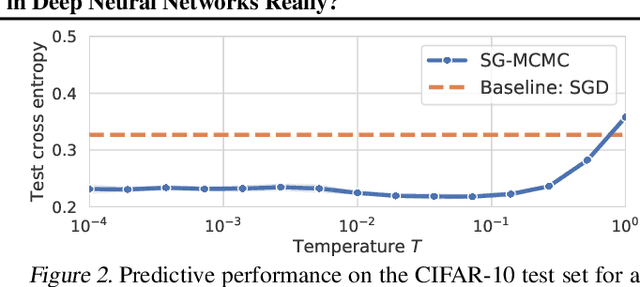
During the past five years the Bayesian deep learning community has developed increasingly accurate and efficient approximate inference procedures that allow for Bayesian inference in deep neural networks. However, despite this algorithmic progress and the promise of improved uncertainty quantification and sample efficiency there are---as of early 2020---no publicized deployments of Bayesian neural networks in industrial practice. In this work we cast doubt on the current understanding of Bayes posteriors in popular deep neural networks: we demonstrate through careful MCMC sampling that the posterior predictive induced by the Bayes posterior yields systematically worse predictions compared to simpler methods including point estimates obtained from SGD. Furthermore, we demonstrate that predictive performance is improved significantly through the use of a "cold posterior" that overcounts evidence. Such cold posteriors sharply deviate from the Bayesian paradigm but are commonly used as heuristic in Bayesian deep learning papers. We put forward several hypotheses that could explain cold posteriors and evaluate the hypotheses through experiments. Our work questions the goal of accurate posterior approximations in Bayesian deep learning: If the true Bayes posterior is poor, what is the use of more accurate approximations? Instead, we argue that it is timely to focus on understanding the origin of the improved performance of cold posteriors.

Hydra: Preserving Ensemble Diversity for Model Distillation

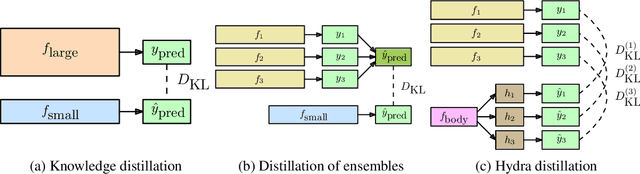
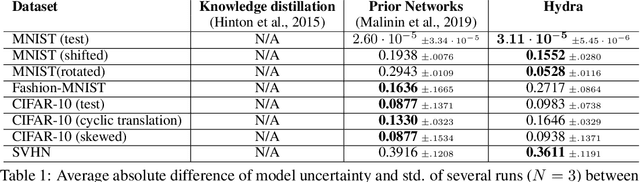
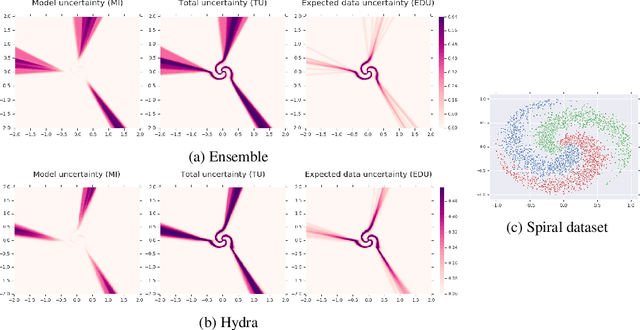
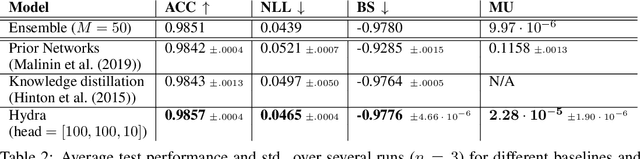
Ensembles of models have been empirically shown to improve predictive performance and to yield robust measures of uncertainty. However, they are expensive in computation and memory. Therefore, recent research has focused on distilling ensembles into a single compact model, reducing the computational and memory burden of the ensemble while trying to preserve its predictive behavior. Most existing distillation formulations summarize the ensemble by capturing its average predictions. As a result, the diversity of the ensemble predictions, stemming from each individual member, is lost. Thus, the distilled model cannot provide a measure of uncertainty comparable to that of the original ensemble. To retain more faithfully the diversity of the ensemble, we propose a distillation method based on a single multi-headed neural network, which we refer to as Hydra. The shared body network learns a joint feature representation that enables each head to capture the predictive behavior of each ensemble member. We demonstrate that with a slight increase in parameter count, Hydra improves distillation performance on classification and regression settings while capturing the uncertainty behaviour of the original ensemble over both in-domain and out-of-distribution tasks.

Adversarial Training Generalizes Data-dependent Spectral Norm Regularization

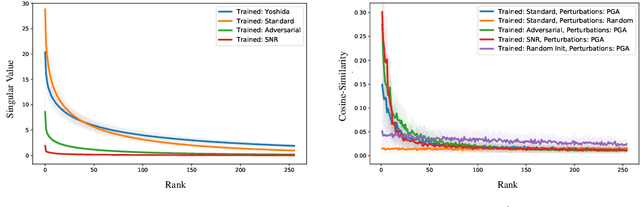
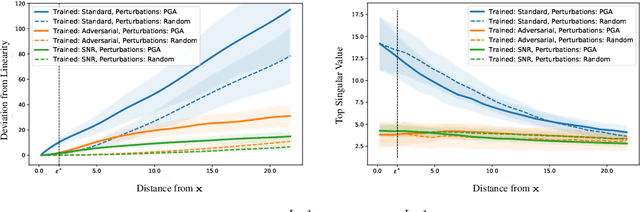
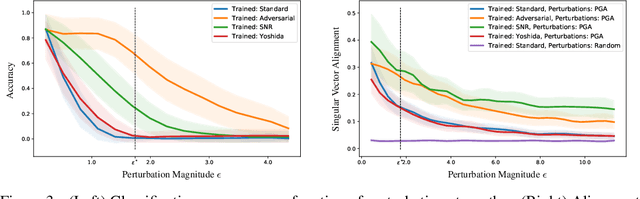
We establish a theoretical link between adversarial training and operator norm regularization for deep neural networks. Specifically, we show that adversarial training is a data-dependent generalization of spectral norm regularization. This intriguing connection provides fundamental insights into the origin of adversarial vulnerability and hints at novel ways to robustify and defend against adversarial attacks. We provide extensive empirical evidence to support our theoretical results.

The Odds are Odd: A Statistical Test for Detecting Adversarial Examples

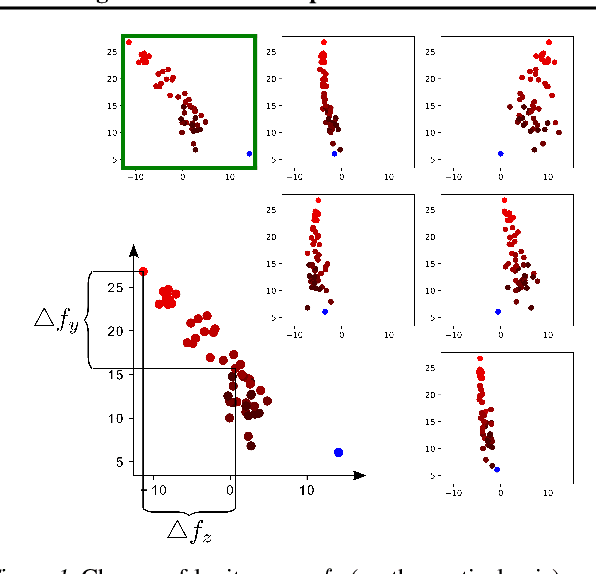
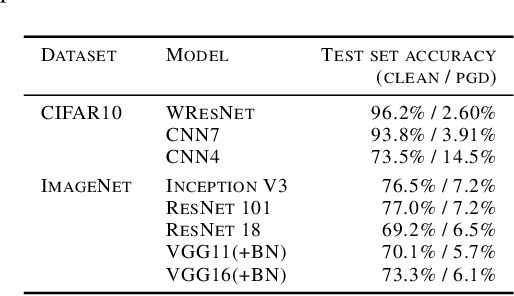
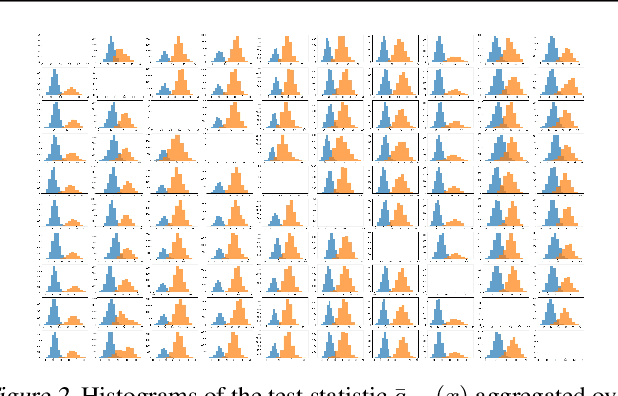
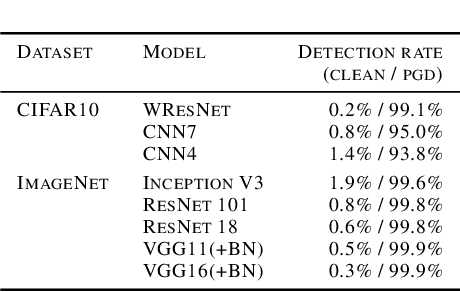
We investigate conditions under which test statistics exist that can reliably detect examples, which have been adversarially manipulated in a white-box attack. These statistics can be easily computed and calibrated by randomly corrupting inputs. They exploit certain anomalies that adversarial attacks introduce, in particular if they follow the paradigm of choosing perturbations optimally under p-norm constraints. Access to the log-odds is the only requirement to defend models. We justify our approach empirically, but also provide conditions under which detectability via the suggested test statistics is guaranteed to be effective. In our experiments, we show that it is even possible to correct test time predictions for adversarial attacks with high accuracy.

Adversarially Robust Training through Structured Gradient Regularization

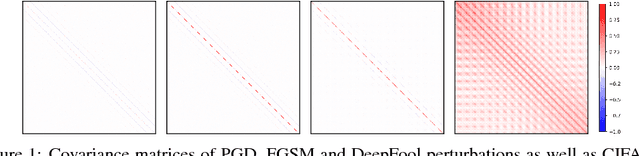
We propose a novel data-dependent structured gradient regularizer to increase the robustness of neural networks vis-a-vis adversarial perturbations. Our regularizer can be derived as a controlled approximation from first principles, leveraging the fundamental link between training with noise and regularization. It adds very little computational overhead during learning and is simple to implement generically in standard deep learning frameworks. Our experiments provide strong evidence that structured gradient regularization can act as an effective first line of defense against attacks based on low-level signal corruption.

Stabilizing Training of Generative Adversarial Networks through Regularization

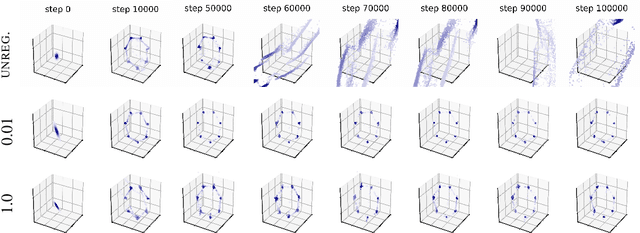
Deep generative models based on Generative Adversarial Networks (GANs) have demonstrated impressive sample quality but in order to work they require a careful choice of architecture, parameter initialization, and selection of hyper-parameters. This fragility is in part due to a dimensional mismatch or non-overlapping support between the model distribution and the data distribution, causing their density ratio and the associated f-divergence to be undefined. We overcome this fundamental limitation and propose a new regularization approach with low computational cost that yields a stable GAN training procedure. We demonstrate the effectiveness of this regularizer across several architectures trained on common benchmark image generation tasks. Our regularization turns GAN models into reliable building blocks for deep learning.