Online Test-time Adaptation for 3D Human Pose Estimation: A Practical Perspective with Estimated 2D Poses

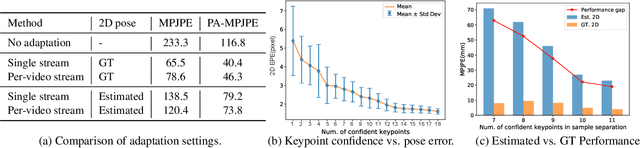
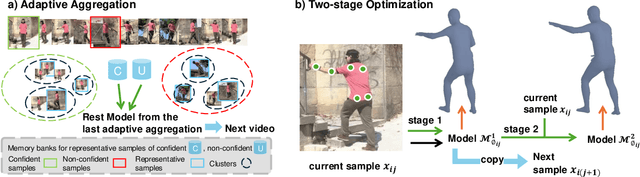
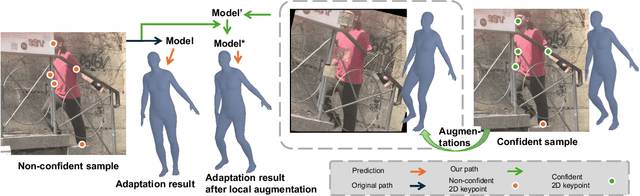
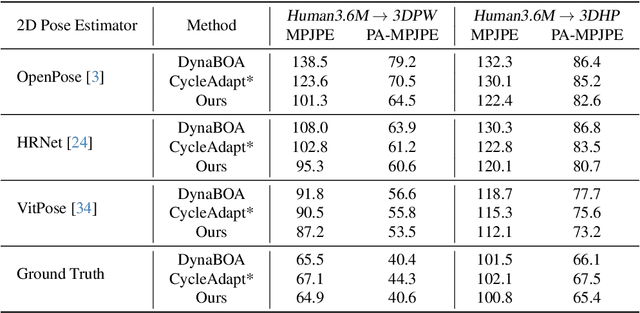
Online test-time adaptation for 3D human pose estimation is used for video streams that differ from training data. Ground truth 2D poses are used for adaptation, but only estimated 2D poses are available in practice. This paper addresses adapting models to streaming videos with estimated 2D poses. Comparing adaptations reveals the challenge of limiting estimation errors while preserving accurate pose information. To this end, we propose adaptive aggregation, a two-stage optimization, and local augmentation for handling varying levels of estimated pose error. First, we perform adaptive aggregation across videos to initialize the model state with labeled representative samples. Within each video, we use a two-stage optimization to benefit from 2D fitting while minimizing the impact of erroneous updates. Second, we employ local augmentation, using adjacent confident samples to update the model before adapting to the current non-confident sample. Our method surpasses state-of-the-art by a large margin, advancing adaptation towards more practical settings of using estimated 2D poses.

OfCaM: Global Human Mesh Recovery via Optimization-free Camera Motion Scale Calibration

Accurate camera motion estimation is critical to estimate human motion in the global space. A standard and widely used method for estimating camera motion is Simultaneous Localization and Mapping (SLAM). However, SLAM only provides a trajectory up to an unknown scale factor. Different from previous attempts that optimize the scale factor, this paper presents Optimization-free Camera Motion Scale Calibration (OfCaM), a novel framework that utilizes prior knowledge from human mesh recovery (HMR) models to directly calibrate the unknown scale factor. Specifically, OfCaM leverages the absolute depth of human-background contact joints from HMR predictions as a calibration reference, enabling the precise recovery of SLAM camera trajectory scale in global space. With this correctly scaled camera motion and HMR's local motion predictions, we achieve more accurate global human motion estimation. To compensate for scenes where we detect SLAM failure, we adopt a local-to-global motion mapping to fuse with previously derived motion to enhance robustness. Simple yet powerful, our method sets a new standard for global human mesh estimation tasks, reducing global human motion error by 60% over the prior SOTA while also demanding orders of magnitude less inference time compared with optimization-based methods.

KITRO: Refining Human Mesh by 2D Clues and Kinematic-tree Rotation

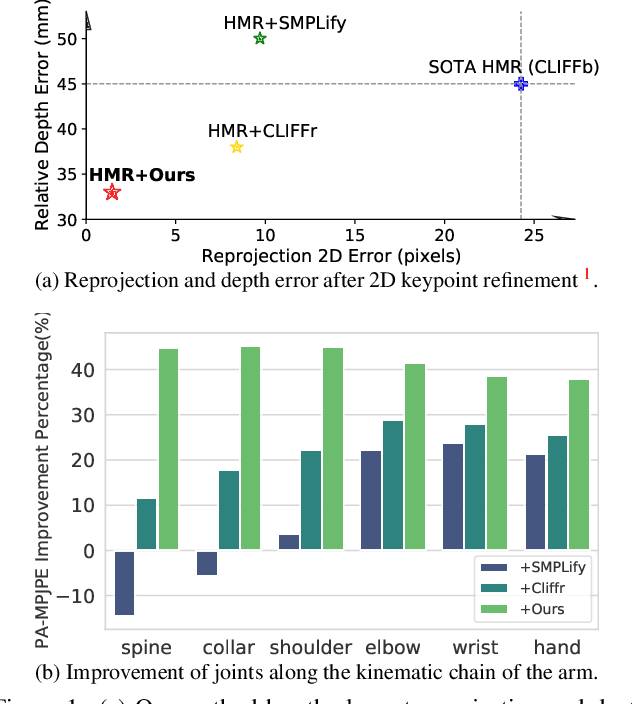
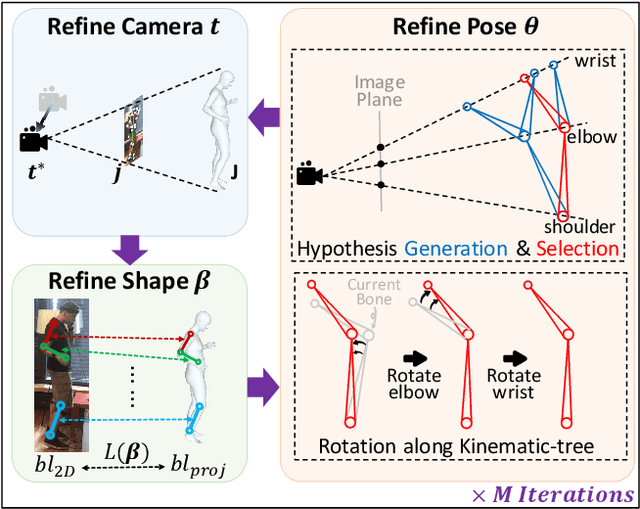
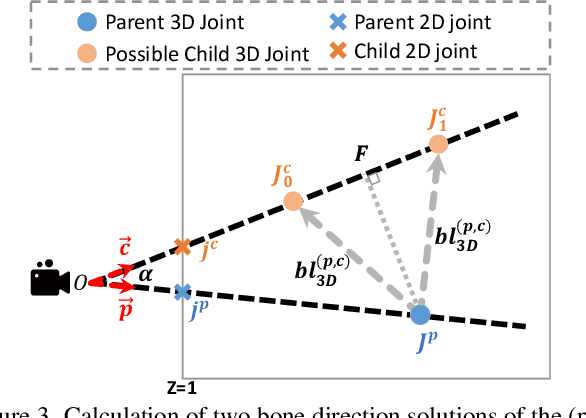
2D keypoints are commonly used as an additional cue to refine estimated 3D human meshes. Current methods optimize the pose and shape parameters with a reprojection loss on the provided 2D keypoints. Such an approach, while simple and intuitive, has limited effectiveness because the optimal solution is hard to find in ambiguous parameter space and may sacrifice depth. Additionally, divergent gradients from distal joints complicate and deviate the refinement of proximal joints in the kinematic chain. To address these, we introduce Kinematic-Tree Rotation (KITRO), a novel mesh refinement strategy that explicitly models depth and human kinematic-tree structure. KITRO treats refinement from a bone-wise perspective. Unlike previous methods which perform gradient-based optimizations, our method calculates bone directions in closed form. By accounting for the 2D pose, bone length, and parent joint's depth, the calculation results in two possible directions for each child joint. We then use a decision tree to trace binary choices for all bones along the human skeleton's kinematic-tree to select the most probable hypothesis. Our experiments across various datasets and baseline models demonstrate that KITRO significantly improves 3D joint estimation accuracy and achieves an ideal 2D fit simultaneously. Our code available at: https://github.com/MartaYang/KITRO.

Learning Unorthogonalized Matrices for Rotation Estimation

Estimating 3D rotations is a common procedure for 3D computer vision. The accuracy depends heavily on the rotation representation. One form of representation -- rotation matrices -- is popular due to its continuity, especially for pose estimation tasks. The learning process usually incorporates orthogonalization to ensure orthonormal matrices. Our work reveals, through gradient analysis, that common orthogonalization procedures based on the Gram-Schmidt process and singular value decomposition will slow down training efficiency. To this end, we advocate removing orthogonalization from the learning process and learning unorthogonalized `Pseudo' Rotation Matrices (PRoM). An optimization analysis shows that PRoM converges faster and to a better solution. By replacing the orthogonalization incorporated representation with our proposed PRoM in various rotation-related tasks, we achieve state-of-the-art results on large-scale benchmarks for human pose estimation.

On the Calibration of Human Pose Estimation

Most 2D human pose estimation frameworks estimate keypoint confidence in an ad-hoc manner, using heuristics such as the maximum value of heatmaps. The confidence is part of the evaluation scheme, e.g., AP for the MSCOCO dataset, yet has been largely overlooked in the development of state-of-the-art methods. This paper takes the first steps in addressing miscalibration in pose estimation. From a calibration point of view, the confidence should be aligned with the pose accuracy. In practice, existing methods are poorly calibrated. We show, through theoretical analysis, why a miscalibration gap exists and how to narrow the gap. Simply predicting the instance size and adjusting the confidence function gives considerable AP improvements. Given the black-box nature of deep neural networks, however, it is not possible to fully close this gap with only closed-form adjustments. As such, we go one step further and learn network-specific adjustments by enforcing consistency between confidence and pose accuracy. Our proposed Calibrated ConfidenceNet (CCNet) is a light-weight post-hoc addition that improves AP by up to 1.4% on off-the-shelf pose estimation frameworks. Applied to the downstream task of mesh recovery, CCNet facilitates an additional 1.0mm decrease in 3D keypoint error.

Bias-Compensated Integral Regression for Human Pose Estimation

In human and hand pose estimation, heatmaps are a crucial intermediate representation for a body or hand keypoint. Two popular methods to decode the heatmap into a final joint coordinate are via an argmax, as done in heatmap detection, or via softmax and expectation, as done in integral regression. Integral regression is learnable end-to-end, but has lower accuracy than detection. This paper uncovers an induced bias from integral regression that results from combining the softmax and the expectation operation. This bias often forces the network to learn degenerately localized heatmaps, obscuring the keypoint's true underlying distribution and leads to lower accuracies. Training-wise, by investigating the gradients of integral regression, we show that the implicit guidance of integral regression to update the heatmap makes it slower to converge than detection. To counter the above two limitations, we propose Bias Compensated Integral Regression (BCIR), an integral regression-based framework that compensates for the bias. BCIR also incorporates a Gaussian prior loss to speed up training and improve prediction accuracy. Experimental results on both the human body and hand benchmarks show that BCIR is faster to train and more accurate than the original integral regression, making it competitive with state-of-the-art detection methods.