Learning Pareto Set for Multi-Objective Continuous Robot Control

For a control problem with multiple conflicting objectives, there exists a set of Pareto-optimal policies called the Pareto set instead of a single optimal policy. When a multi-objective control problem is continuous and complex, traditional multi-objective reinforcement learning (MORL) algorithms search for many Pareto-optimal deep policies to approximate the Pareto set, which is quite resource-consuming. In this paper, we propose a simple and resource-efficient MORL algorithm that learns a continuous representation of the Pareto set in a high-dimensional policy parameter space using a single hypernet. The learned hypernet can directly generate various well-trained policy networks for different user preferences. We compare our method with two state-of-the-art MORL algorithms on seven multi-objective continuous robot control problems. Experimental results show that our method achieves the best overall performance with the least training parameters. An interesting observation is that the Pareto set is well approximated by a curved line or surface in a high-dimensional parameter space. This observation will provide insight for researchers to design new MORL algorithms.

DiffMAC: Diffusion Manifold Hallucination Correction for High Generalization Blind Face Restoration

Blind face restoration (BFR) is a highly challenging problem due to the uncertainty of degradation patterns. Current methods have low generalization across photorealistic and heterogeneous domains. In this paper, we propose a Diffusion-Information-Diffusion (DID) framework to tackle diffusion manifold hallucination correction (DiffMAC), which achieves high-generalization face restoration in diverse degraded scenes and heterogeneous domains. Specifically, the first diffusion stage aligns the restored face with spatial feature embedding of the low-quality face based on AdaIN, which synthesizes degradation-removal results but with uncontrollable artifacts for some hard cases. Based on Stage I, Stage II considers information compression using manifold information bottleneck (MIB) and finetunes the first diffusion model to improve facial fidelity. DiffMAC effectively fights against blind degradation patterns and synthesizes high-quality faces with attribute and identity consistencies. Experimental results demonstrate the superiority of DiffMAC over state-of-the-art methods, with a high degree of generalization in real-world and heterogeneous settings. The source code and models will be public.

Effects of Archive Size on Computation Time and Solution Quality for Multi-Objective Optimization

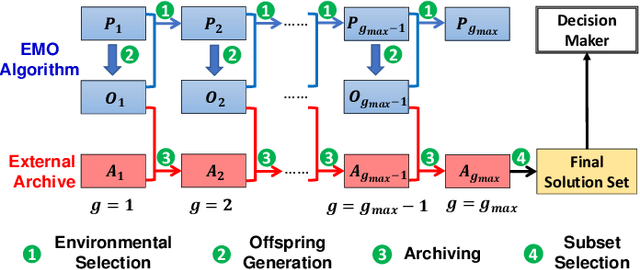
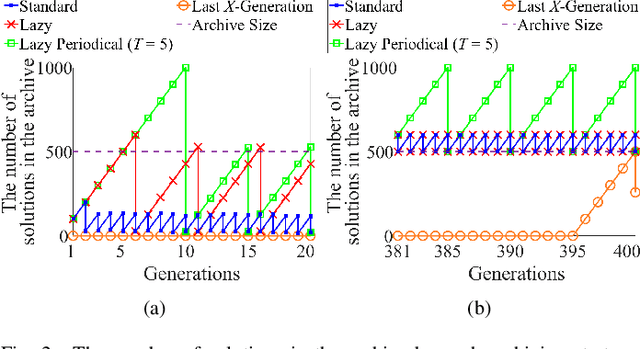
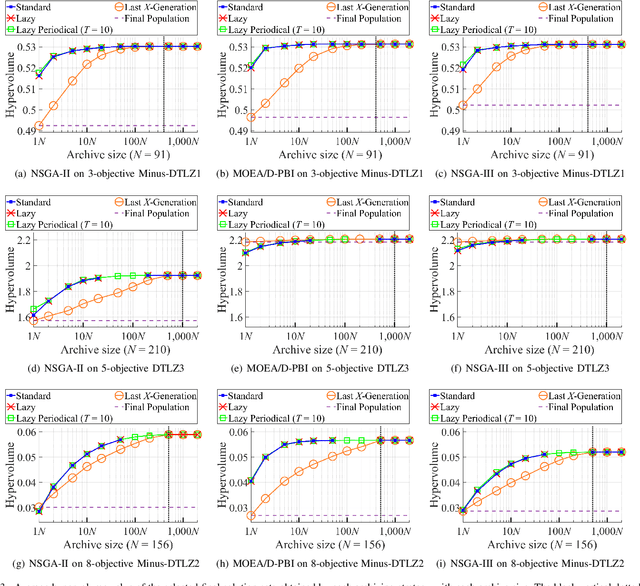
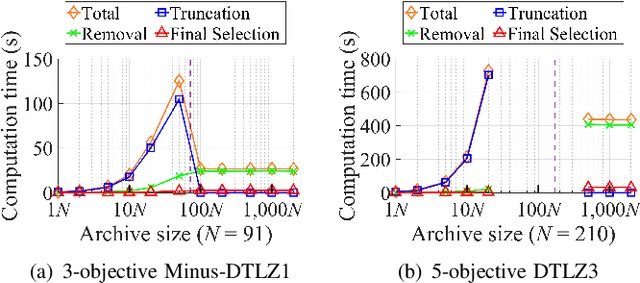
An unbounded external archive has been used to store all nondominated solutions found by an evolutionary multi-objective optimization algorithm in some studies. It has been shown that a selected solution subset from the stored solutions is often better than the final population. However, the use of the unbounded archive is not always realistic. When the number of examined solutions is huge, we must pre-specify the archive size. In this study, we examine the effects of the archive size on three aspects: (i) the quality of the selected final solution set, (ii) the total computation time for the archive maintenance and the final solution set selection, and (iii) the required memory size. Unsurprisingly, the increase of the archive size improves the final solution set quality. Interestingly, the total computation time of a medium-size archive is much larger than that of a small-size archive and a huge-size archive (e.g., an unbounded archive). To decrease the computation time, we examine two ideas: periodical archive update and archiving only in later generations. Compared with updating the archive at every generation, the first idea can obtain almost the same final solution set quality using a much shorter computation time at the cost of a slight increase of the memory size. The second idea drastically decreases the computation time at the cost of a slight deterioration of the final solution set quality. Based on our experimental results, some suggestions are given about how to appropriately choose an archiving strategy and an archive size.

HV-Net: Hypervolume Approximation based on DeepSets

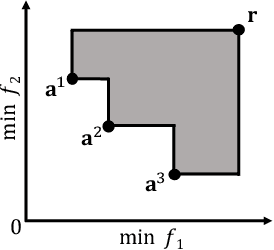
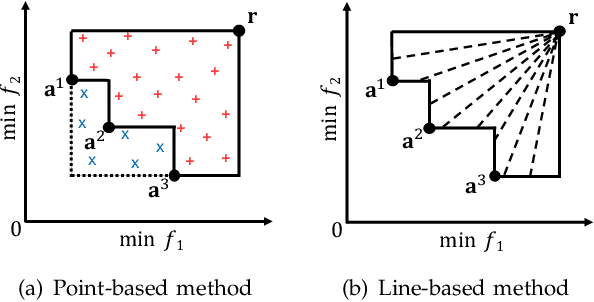
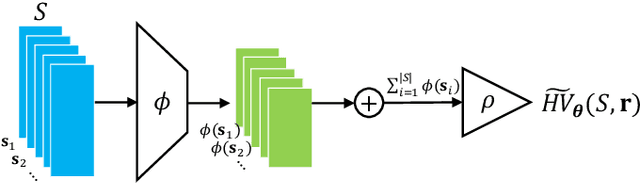
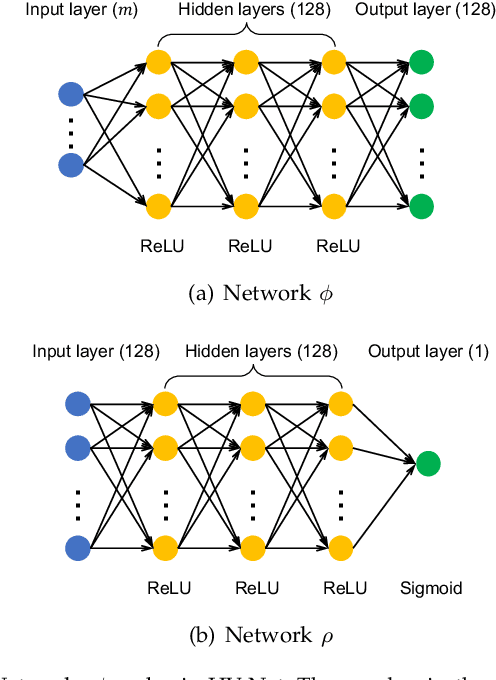
In this letter, we propose HV-Net, a new method for hypervolume approximation in evolutionary multi-objective optimization. The basic idea of HV-Net is to use DeepSets, a deep neural network with permutation invariant property, to approximate the hypervolume of a non-dominated solution set. The input of HV-Net is a non-dominated solution set in the objective space, and the output is an approximated hypervolume value of this solution set. The performance of HV-Net is evaluated through computational experiments by comparing it with two commonly-used hypervolume approximation methods (i.e., point-based method and line-based method). Our experimental results show that HV-Net outperforms the other two methods in terms of both the approximation error and the runtime, which shows the potential of using deep learning technique for hypervolume approximation.

Learning to Approximate: Auto Direction Vector Set Generation for Hypervolume Contribution Approximation

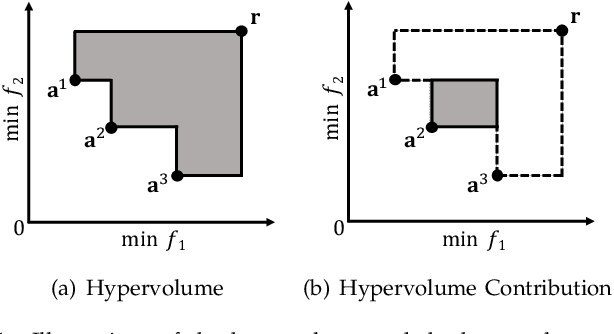
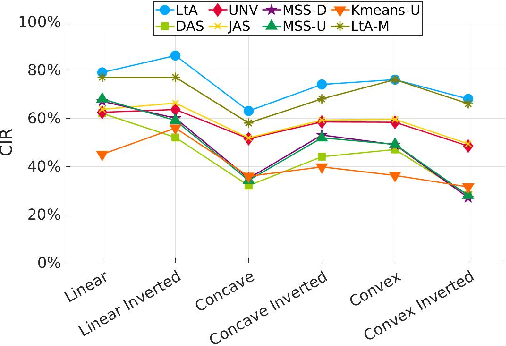
Hypervolume contribution is an important concept in evolutionary multi-objective optimization (EMO). It involves in hypervolume-based EMO algorithms and hypervolume subset selection algorithms. Its main drawback is that it is computationally expensive in high-dimensional spaces, which limits its applicability to many-objective optimization. Recently, an R2 indicator variant (i.e., $R_2^{\text{HVC}}$ indicator) is proposed to approximate the hypervolume contribution. The $R_2^{\text{HVC}}$ indicator uses line segments along a number of direction vectors for hypervolume contribution approximation. It has been shown that different direction vector sets lead to different approximation quality. In this paper, we propose \textit{Learning to Approximate (LtA)}, a direction vector set generation method for the $R_2^{\text{HVC}}$ indicator. The direction vector set is automatically learned from training data. The learned direction vector set can then be used in the $R_2^{\text{HVC}}$ indicator to improve its approximation quality. The usefulness of the proposed LtA method is examined by comparing it with other commonly-used direction vector set generation methods for the $R_2^{\text{HVC}}$ indicator. Experimental results suggest the superiority of LtA over the other methods for generating high quality direction vector sets.

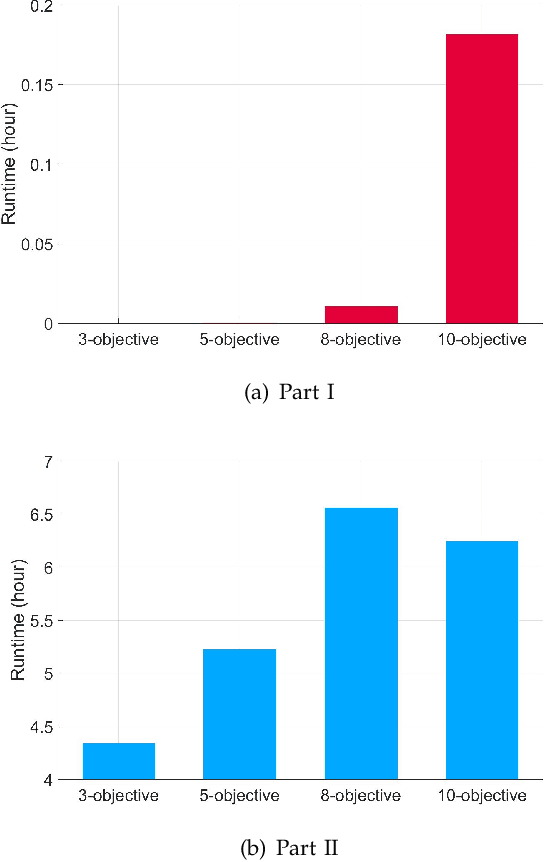
Benchmarking Subset Selection from Large Candidate Solution Sets in Evolutionary Multi-objective Optimization

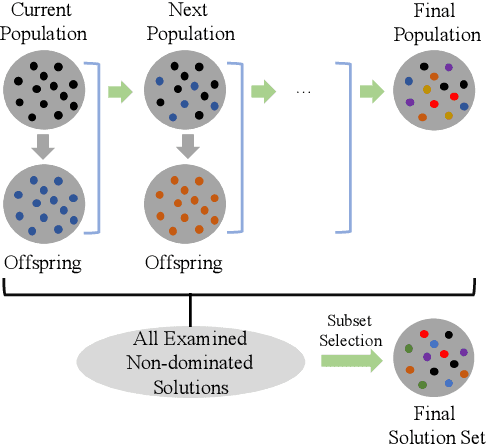
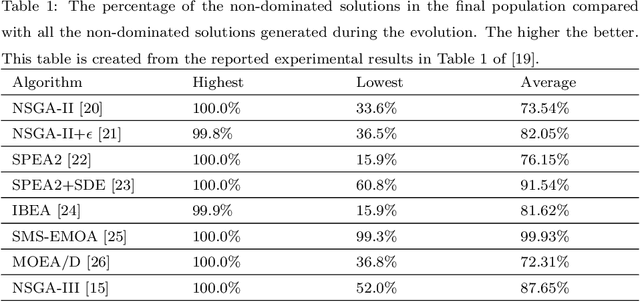
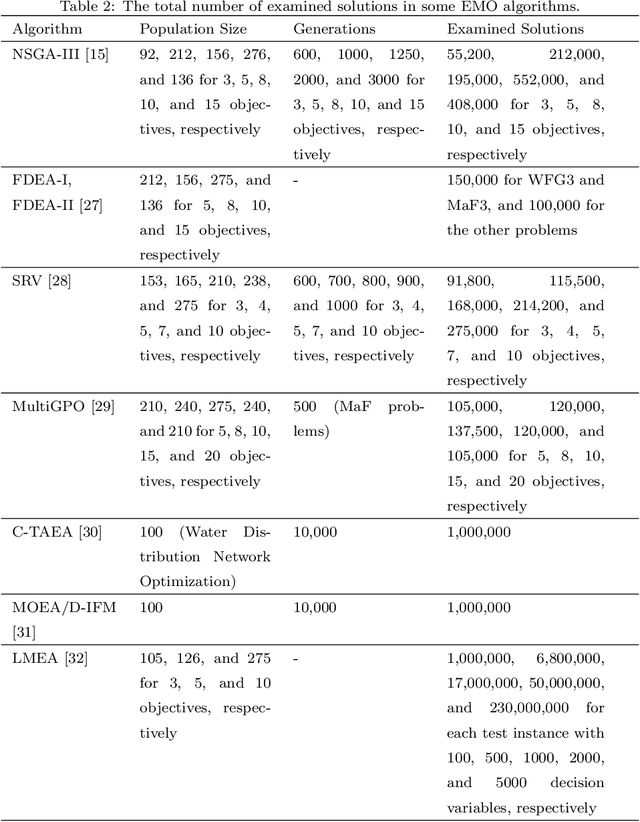
In the evolutionary multi-objective optimization (EMO) field, the standard practice is to present the final population of an EMO algorithm as the output. However, it has been shown that the final population often includes solutions which are dominated by other solutions generated and discarded in previous generations. Recently, a new EMO framework has been proposed to solve this issue by storing all the non-dominated solutions generated during the evolution in an archive and selecting a subset of solutions from the archive as the output. The key component in this framework is the subset selection from the archive which usually stores a large number of candidate solutions. However, most studies on subset selection focus on small candidate solution sets for environmental selection. There is no benchmark test suite for large-scale subset selection. This paper aims to fill this research gap by proposing a benchmark test suite for subset selection from large candidate solution sets, and comparing some representative methods using the proposed test suite. The proposed test suite together with the benchmarking studies provides a baseline for researchers to understand, use, compare, and develop subset selection methods in the EMO field.

Clustering-Based Subset Selection in Evolutionary Multiobjective Optimization

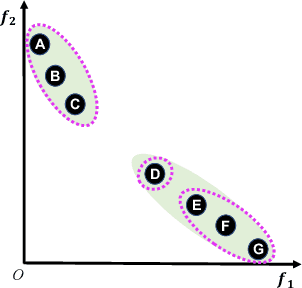
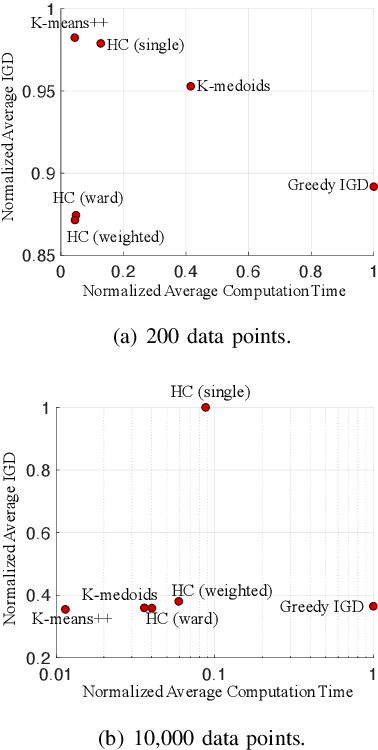
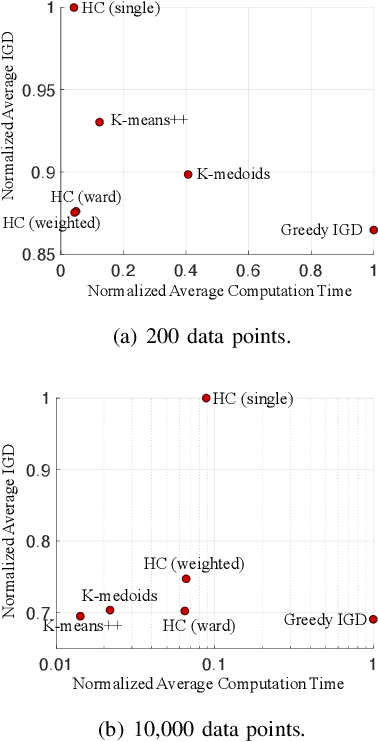
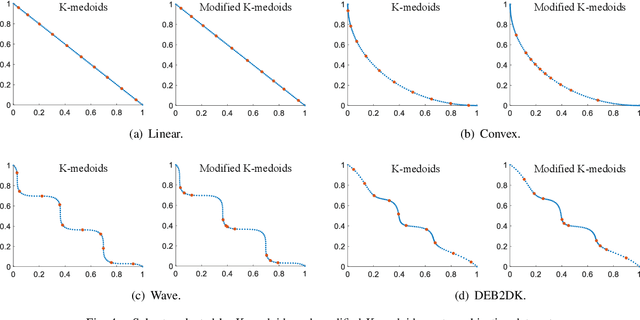
Subset selection is an important component in evolutionary multiobjective optimization (EMO) algorithms. Clustering, as a classic method to group similar data points together, has been used for subset selection in some fields. However, clustering-based methods have not been evaluated in the context of subset selection from solution sets obtained by EMO algorithms. In this paper, we first review some classic clustering algorithms. We also point out that another popular subset selection method, i.e., inverted generational distance (IGD)-based subset selection, can be viewed as clustering. Then, we perform a comprehensive experimental study to evaluate the performance of various clustering algorithms in different scenarios. Experimental results are analyzed in detail, and some suggestions about the use of clustering algorithms for subset selection are derived. Additionally, we demonstrate that decision maker's preference can be introduced to clustering-based subset selection.

Hypervolume-Optimal $μ$-Distributions on Line/Plane-based Pareto Fronts in Three Dimensions

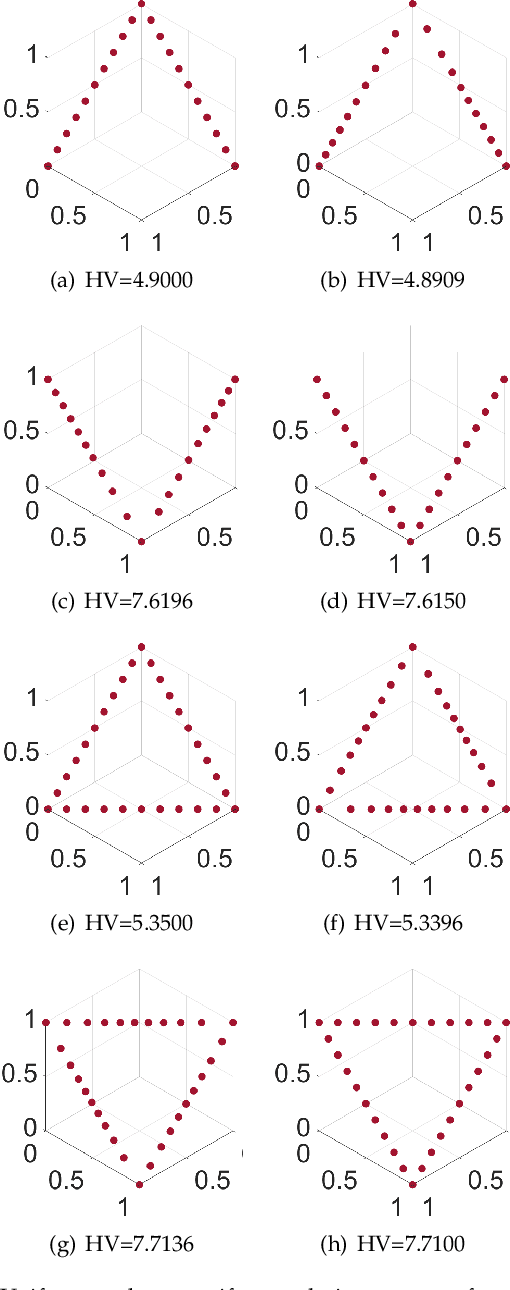
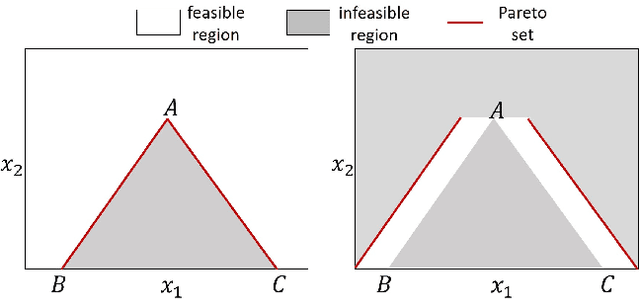
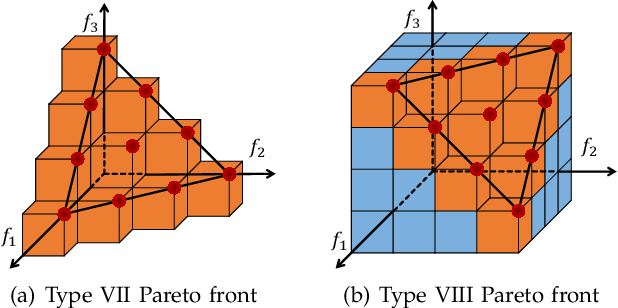
Hypervolume is widely used in the evolutionary multi-objective optimization (EMO) field to evaluate the quality of a solution set. For a solution set with $\mu$ solutions on a Pareto front, a larger hypervolume means a better solution set. Investigating the distribution of the solution set with the largest hypervolume is an important topic in EMO, which is the so-called hypervolume optimal $\mu$-distribution. Theoretical results have shown that the $\mu$ solutions are uniformly distributed on a linear Pareto front in two dimensions. However, the $\mu$ solutions are not always uniformly distributed on a single-line Pareto front in three dimensions. They are only uniform when the single-line Pareto front has one constant objective. In this paper, we further investigate the hypervolume optimal $\mu$-distribution in three dimensions. We consider the line- and plane-based Pareto fronts. For the line-based Pareto fronts, we extend the single-line Pareto front to two-line and three-line Pareto fronts, where each line has one constant objective. For the plane-based Pareto fronts, the linear triangular and inverted triangular Pareto fronts are considered. First, we show that the $\mu$ solutions are not always uniformly distributed on the line-based Pareto fronts. The uniformity depends on how the lines are combined. Then, we show that a uniform solution set on the plane-based Pareto front is not always optimal for hypervolume maximization. It is locally optimal with respect to a $(\mu+1)$ selection scheme. Our results can help researchers in the community to better understand and utilize the hypervolume indicator.

Fast Greedy Subset Selection from Large Candidate Solution Sets in Evolutionary Multi-objective Optimization

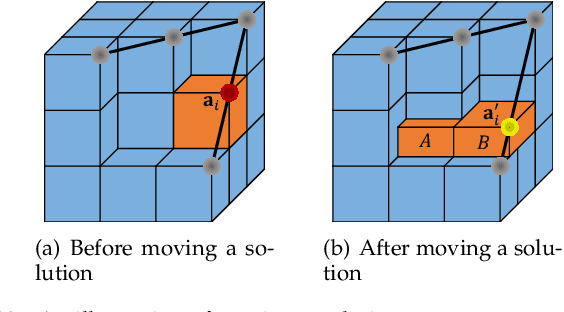
Subset selection is an interesting and important topic in the field of evolutionary multi-objective optimization (EMO). Especially, in an EMO algorithm with an unbounded external archive, subset selection is an essential post-processing procedure to select a pre-specified number of solutions as the final result. In this paper, we discuss the efficiency of greedy subset selection for the hypervolume, IGD and IGD+ indicators. Greedy algorithms usually efficiently handle subset selection. However, when a large number of solutions are given (e.g., subset selection from tens of thousands of solutions in an unbounded external archive), they often become time-consuming. Our idea is to use the submodular property, which is known for the hypervolume indicator, to improve their efficiency. First, we prove that the IGD and IGD+ indicators are also submodular. Next, based on the submodular property, we propose an efficient greedy inclusion algorithm for each indicator. Then, we demonstrate through computational experiments that the proposed algorithms are much faster than the standard greedy subset selection algorithms.

Evolutionary Multi-Objective Optimization Algorithm Framework with Three Solution Sets

It is assumed in the evolutionary multi-objective optimization (EMO) community that a final solution is selected by a decision maker from a non-dominated solution set obtained by an EMO algorithm. The number of solutions to be presented to the decision maker can be totally different. In some cases, the decision maker may want to examine only a few representative solutions from which a final solution is selected. In other cases, a large number of non-dominated solutions may be needed to visualize the Pareto front. In this paper, we suggest the use of a general EMO framework with three solution sets to handle various situations with respect to the required number of solutions. The three solution sets are the main population of an EMO algorithm, an external archive to store promising solutions, and a final solution set which is presented to the decision maker. The final solution set is selected from the archive. Thus the population size and the archive size can be arbitrarily specified as long as the archive size is not smaller than the required number of solutions. The final population is not necessarily to be a good solution set since it is not presented to the decision maker. Through computational experiments, we show the advantages of this framework over the standard final population and final archive frameworks. We also discuss how to select a final solution set and how to explain the reason for the selection, which is the first attempt towards an explainable EMO framework.