Lie Meng Pang
Optimal Distribution of Solutions for Crowding Distance on Linear Pareto Fronts of Two-Objective Optimization Problems
Apr 24, 2025Abstract:Characteristics of an evolutionary multi-objective optimization (EMO) algorithm can be explained using its best solution set. For example, the best solution set for SMS-EMOA is the same as the optimal distribution of solutions for hypervolume maximization. For NSGA-III, if the Pareto front has intersection points with all reference lines, all of those intersection points are the best solution set. For MOEA/D, the best solution set is the set of the optimal solution of each sub-problem. Whereas these EMO algorithms can be analyzed in this manner, the best solution set for the most well-known and frequently-used EMO algorithm NSGA-II has not been discussed in the literature. This is because NSGA-II is not based on any clear criterion to be optimized (e.g., hypervolume maximization, distance minimization to the nearest reference line). As the first step toward the best solution set analysis for NSGA-II, we discuss the optimal distribution of solutions for the crowding distance under the simplest setting: the maximization of the minimum crowding distance on linear Pareto fronts of two-objective optimization problems. That is, we discuss the optimal distribution of solutions on a straight line. Our theoretical analysis shows that the uniformly distributed solutions are not the best solution set. However, it is also shown by computational experiments that the uniformly distributed solutions (except for the duplicated two extreme solutions at each edge of the Pareto front) are obtained from a modified NSGA-II with the ($\mu$ + 1) generation update scheme.
When to Truncate the Archive? On the Effect of the Truncation Frequency in Multi-Objective Optimisation
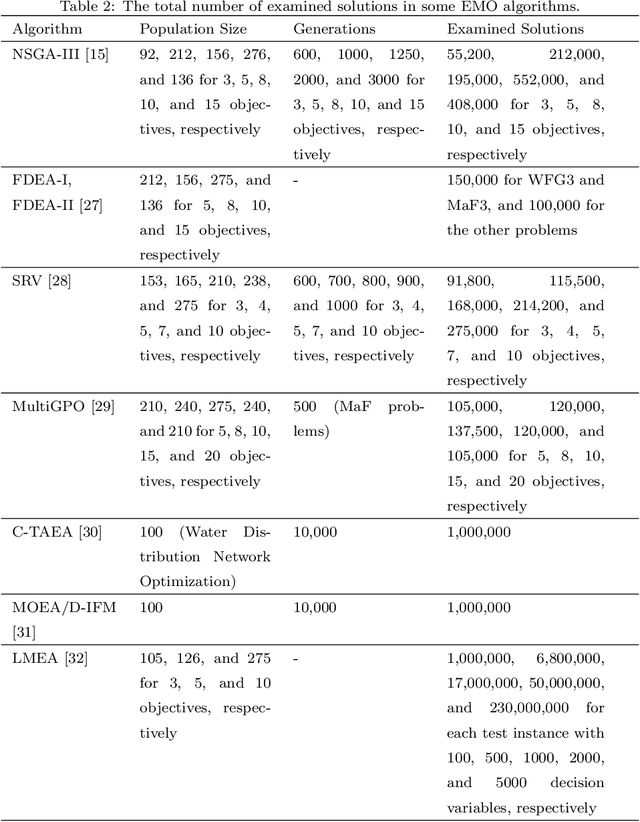
Apr 02, 2025Abstract:Using an archive to store nondominated solutions found during the search of a multi-objective evolutionary algorithm (MOEA) is a useful practice. However, as nondominated solutions of a multi-objective optimisation problem can be enormous or infinitely many, it is desirable to provide the decision-maker with only a small, representative portion of all the nondominated solutions in the archive, thus entailing a truncation operation. Then, an important issue is when to truncate the archive. This can be done once a new solution generated, a batch of new solutions generated, or even using an unbounded archive to keep all nondominated solutions generated and truncate it later. Intuitively, the last approach may lead to a better result since we have all the information in hand before performing the truncation. In this paper, we study this issue and investigate the effect of the timing of truncating the archive. We apply well-established truncation criteria that are commonly used in the population maintenance procedure of MOEAs (e.g., crowding distance, hypervolume indicator, and decomposition). We show that, interestingly, truncating the archive once a new solution generated tends to be the best, whereas considering an unbounded archive is often the worst. We analyse and discuss this phenomenon. Our results highlight the importance of developing effective subset selection techniques (rather than employing the population maintenance methods in MOEAs) when using a large archive.
Large Language Model-Based Benchmarking Experiment Settings for Evolutionary Multi-Objective Optimization
Feb 28, 2025Abstract:When we manually design an evolutionary optimization algorithm, we implicitly or explicitly assume a set of target optimization problems. In the case of automated algorithm design, target optimization problems are usually explicitly shown. Recently, the use of large language models (LLMs) for the design of evolutionary multi-objective optimization (EMO) algorithms have been examined in some studies. In those studies, target multi-objective problems are not always explicitly shown. It is well known in the EMO community that the performance evaluation results of EMO algorithms depend on not only test problems but also many other factors such as performance indicators, reference point, termination condition, and population size. Thus, it is likely that the designed EMO algorithms by LLMs depends on those factors. In this paper, we try to examine the implicit assumption about the performance comparison of EMO algorithms in LLMs. For this purpose, we ask LLMs to design a benchmarking experiment of EMO algorithms. Our experiments show that LLMs often suggest classical benchmark settings: Performance examination of NSGA-II, MOEA/D and NSGA-III on ZDT, DTLZ and WFG by HV and IGD under the standard parameter specifications.
Benchmarking Subset Selection from Large Candidate Solution Sets in Evolutionary Multi-objective Optimization
Jan 18, 2022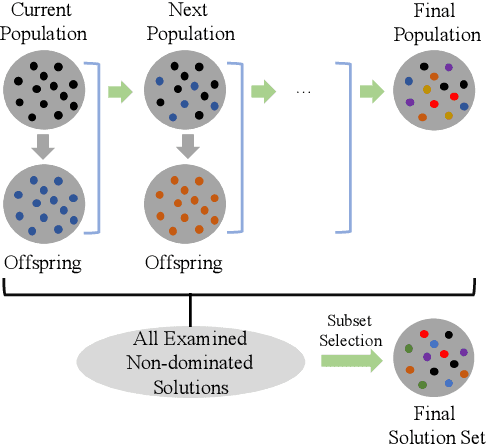

Abstract:In the evolutionary multi-objective optimization (EMO) field, the standard practice is to present the final population of an EMO algorithm as the output. However, it has been shown that the final population often includes solutions which are dominated by other solutions generated and discarded in previous generations. Recently, a new EMO framework has been proposed to solve this issue by storing all the non-dominated solutions generated during the evolution in an archive and selecting a subset of solutions from the archive as the output. The key component in this framework is the subset selection from the archive which usually stores a large number of candidate solutions. However, most studies on subset selection focus on small candidate solution sets for environmental selection. There is no benchmark test suite for large-scale subset selection. This paper aims to fill this research gap by proposing a benchmark test suite for subset selection from large candidate solution sets, and comparing some representative methods using the proposed test suite. The proposed test suite together with the benchmarking studies provides a baseline for researchers to understand, use, compare, and develop subset selection methods in the EMO field.
Evolutionary Multi-Objective Optimization Algorithm Framework with Three Solution Sets
Dec 14, 2020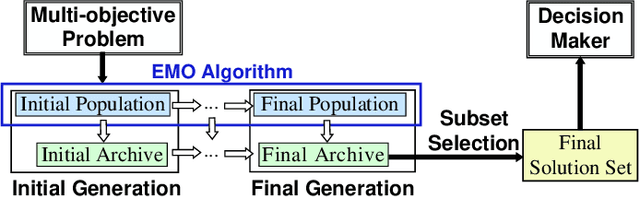

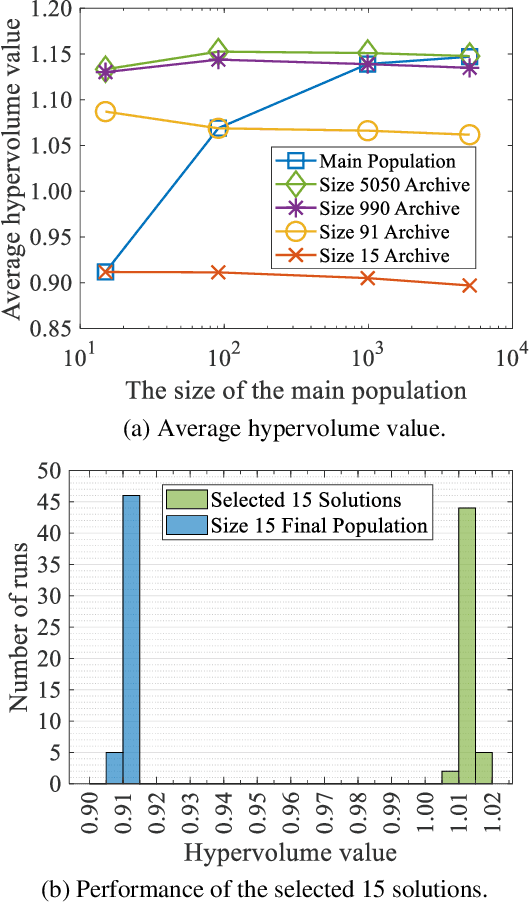
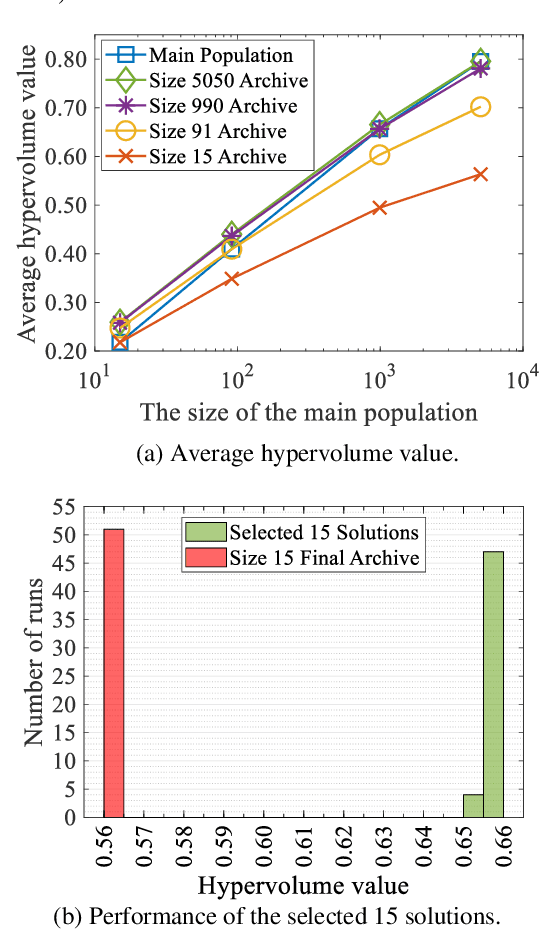
Abstract:It is assumed in the evolutionary multi-objective optimization (EMO) community that a final solution is selected by a decision maker from a non-dominated solution set obtained by an EMO algorithm. The number of solutions to be presented to the decision maker can be totally different. In some cases, the decision maker may want to examine only a few representative solutions from which a final solution is selected. In other cases, a large number of non-dominated solutions may be needed to visualize the Pareto front. In this paper, we suggest the use of a general EMO framework with three solution sets to handle various situations with respect to the required number of solutions. The three solution sets are the main population of an EMO algorithm, an external archive to store promising solutions, and a final solution set which is presented to the decision maker. The final solution set is selected from the archive. Thus the population size and the archive size can be arbitrarily specified as long as the archive size is not smaller than the required number of solutions. The final population is not necessarily to be a good solution set since it is not presented to the decision maker. Through computational experiments, we show the advantages of this framework over the standard final population and final archive frameworks. We also discuss how to select a final solution set and how to explain the reason for the selection, which is the first attempt towards an explainable EMO framework.
Decomposition-Based Multi-Objective Evolutionary Algorithm Design under Two Algorithm Frameworks
Aug 17, 2020Abstract:The development of efficient and effective evolutionary multi-objective optimization (EMO) algorithms has been an active research topic in the evolutionary computation community. Over the years, many EMO algorithms have been proposed. The existing EMO algorithms are mainly developed based on the final population framework. In the final population framework, the final population of an EMO algorithm is presented to the decision maker. Thus, it is required that the final population produced by an EMO algorithm is a good solution set. Recently, the use of solution selection framework was suggested for the design of EMO algorithms. This framework has an unbounded external archive to store all the examined solutions. A pre-specified number of solutions are selected from the archive as the final solutions presented to the decision maker. When the solution selection framework is used, EMO algorithms can be designed in a more flexible manner since the final population is not necessarily to be a good solution set. In this paper, we examine the design of MOEA/D under these two frameworks. We use an offline genetic algorithm-based hyper-heuristic method to find the optimal configuration of MOEA/D in each framework. The DTLZ and WFG test suites and their minus versions are used in our experiments. The experimental results suggest the possibility that a more flexible, robust and high-performance MOEA/D algorithm can be obtained when the solution selection framework is used.
Algorithm Configurations of MOEA/D with an Unbounded External Archive
Jul 27, 2020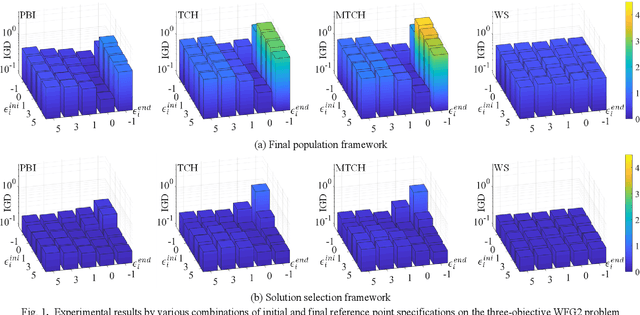
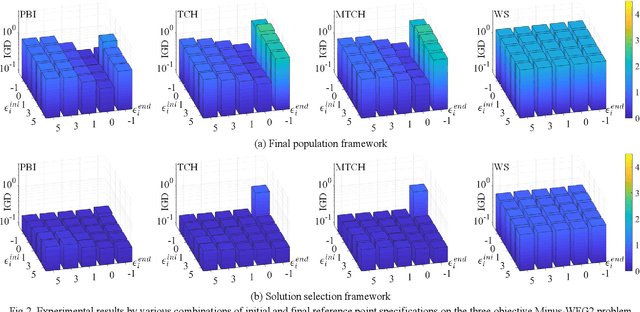
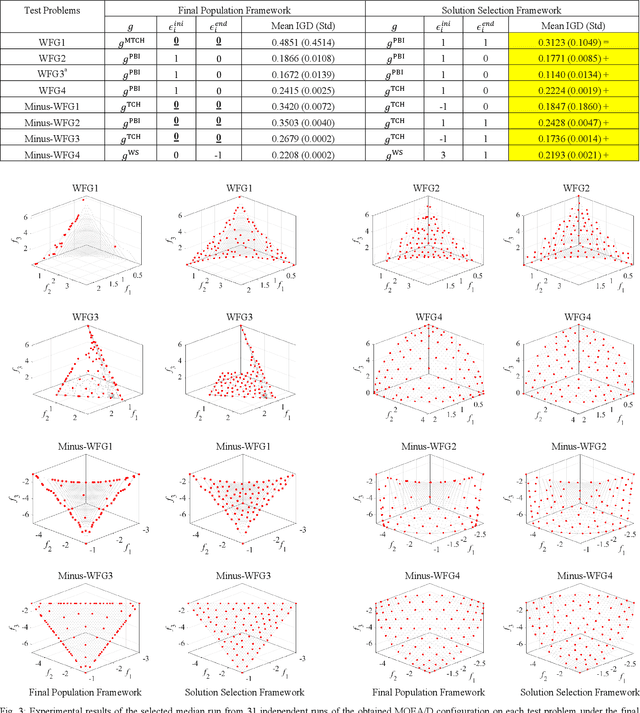
Abstract:In the evolutionary multi-objective optimization (EMO) community, it is usually assumed that the final population is presented to the decision maker as the result of the execution of an EMO algorithm. Recently, an unbounded external archive was used to evaluate the performance of EMO algorithms in some studies where a pre-specified number of solutions are selected from all the examined non-dominated solutions. In this framework, which is referred to as the solution selection framework, the final population does not have to be a good solution set. Thus, the solution selection framework offers higher flexibility to the design of EMO algorithms than the final population framework. In this paper, we examine the design of MOEA/D under these two frameworks. First, we show that the performance of MOEA/D is improved by linearly changing the reference point specification during its execution through computational experiments with various combinations of initial and final specifications. Robust and high performance of the solution selection framework is observed. Then, we examine the use of a genetic algorithm-based offline hyper-heuristic method to find the best configuration of MOEA/D in each framework. Finally, we further discuss solution selection after the execution of an EMO algorithm in the solution selection framework.
Solution Subset Selection for Final Decision Making in Evolutionary Multi-Objective Optimization
Jun 15, 2020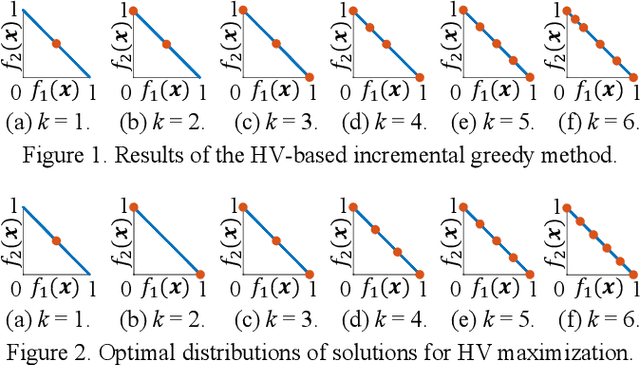
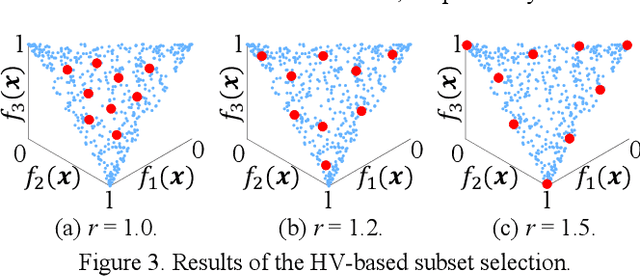
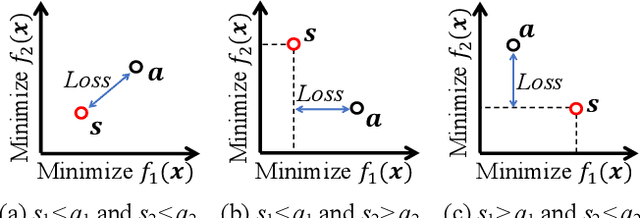
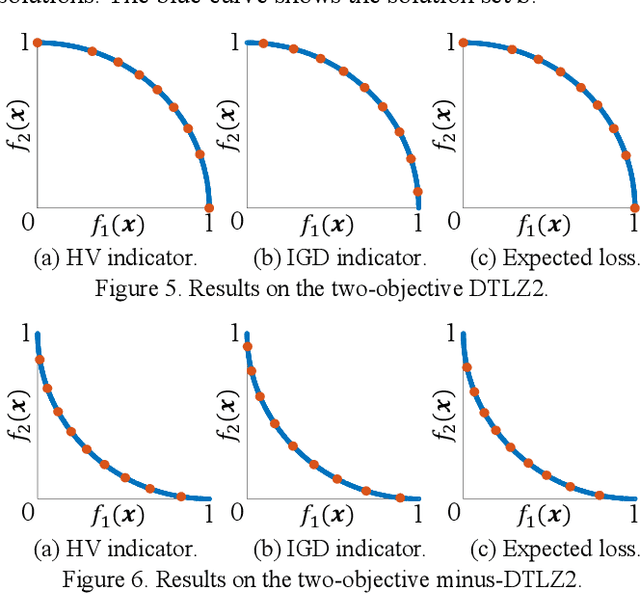
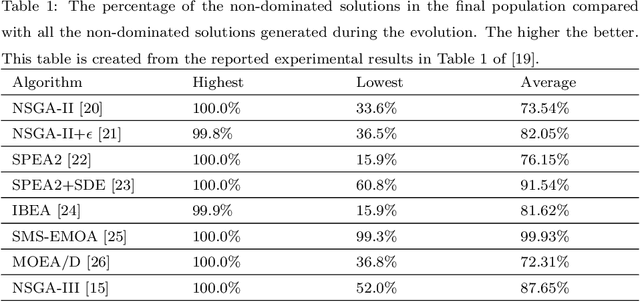
Abstract:In general, a multi-objective optimization problem does not have a single optimal solution but a set of Pareto optimal solutions, which forms the Pareto front in the objective space. Various evolutionary algorithms have been proposed to approximate the Pareto front using a pre-specified number of solutions. Hundreds of solutions are obtained by their single run. The selection of a single final solution from the obtained solutions is assumed to be done by a human decision maker. However, in many cases, the decision maker does not want to examine hundreds of solutions. Thus, it is needed to select a small subset of the obtained solutions. In this paper, we discuss subset selection from a viewpoint of the final decision making. First we briefly explain existing subset selection studies. Next we formulate an expected loss function for subset selection. We also show that the formulated function is the same as the IGD plus indicator. Then we report experimental results where the proposed approach is compared with other indicator-based subset selection methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge