Prompt Learning for Generalized Vehicle Routing

Neural combinatorial optimization (NCO) is a promising learning-based approach to solving various vehicle routing problems without much manual algorithm design. However, the current NCO methods mainly focus on the in-distribution performance, while the real-world problem instances usually come from different distributions. A costly fine-tuning approach or generalized model retraining from scratch could be needed to tackle the out-of-distribution instances. Unlike the existing methods, this work investigates an efficient prompt learning approach in NCO for cross-distribution adaptation. To be concrete, we propose a novel prompt learning method to facilitate fast zero-shot adaptation of a pre-trained model to solve routing problem instances from different distributions. The proposed model learns a set of prompts among various distributions and then selects the best-matched one to prompt a pre-trained attention model for each problem instance. Extensive experiments show that the proposed prompt learning approach facilitates the fast adaptation of pre-trained routing models. It also outperforms existing generalized models on both in-distribution prediction and zero-shot generalization to a diverse set of new tasks. Our code implementation is available online https://github.com/FeiLiu36/PromptVRP.

Data-Driven Preference Sampling for Pareto Front Learning

Pareto front learning is a technique that introduces preference vectors in a neural network to approximate the Pareto front. Previous Pareto front learning methods have demonstrated high performance in approximating simple Pareto fronts. These methods often sample preference vectors from a fixed Dirichlet distribution. However, no fixed sampling distribution can be adapted to diverse Pareto fronts. Efficiently sampling preference vectors and accurately estimating the Pareto front is a challenge. To address this challenge, we propose a data-driven preference vector sampling framework for Pareto front learning. We utilize the posterior information of the objective functions to adjust the parameters of the sampling distribution flexibly. In this manner, the proposed method can sample preference vectors from the location of the Pareto front with a high probability. Moreover, we design the distribution of the preference vector as a mixture of Dirichlet distributions to improve the performance of the model in disconnected Pareto fronts. Extensive experiments validate the superiority of the proposed method compared with state-of-the-art algorithms.

HV-Net: Hypervolume Approximation based on DeepSets

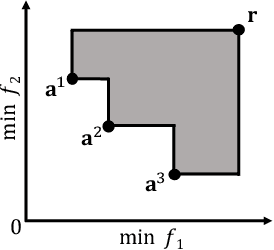
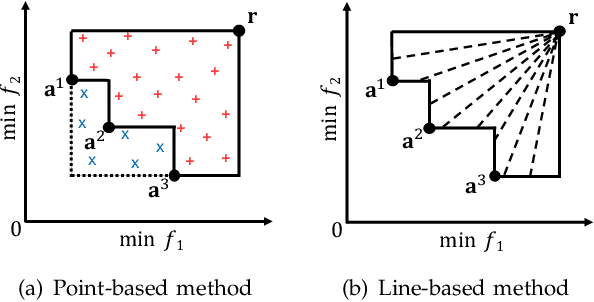
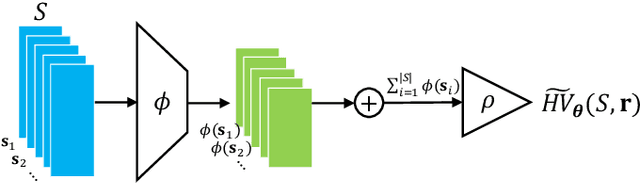
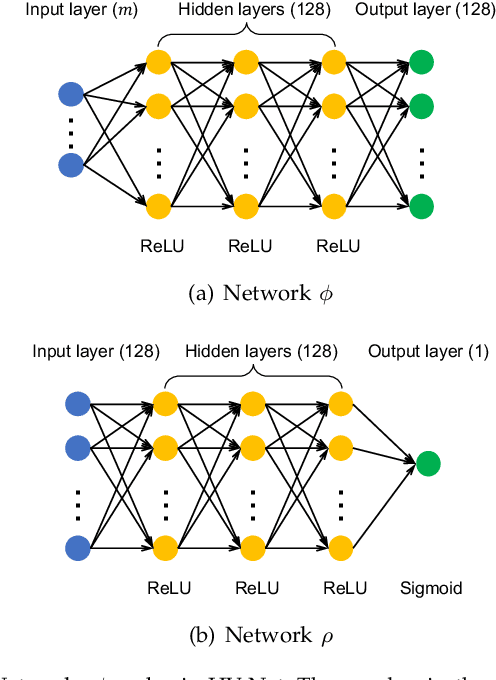
In this letter, we propose HV-Net, a new method for hypervolume approximation in evolutionary multi-objective optimization. The basic idea of HV-Net is to use DeepSets, a deep neural network with permutation invariant property, to approximate the hypervolume of a non-dominated solution set. The input of HV-Net is a non-dominated solution set in the objective space, and the output is an approximated hypervolume value of this solution set. The performance of HV-Net is evaluated through computational experiments by comparing it with two commonly-used hypervolume approximation methods (i.e., point-based method and line-based method). Our experimental results show that HV-Net outperforms the other two methods in terms of both the approximation error and the runtime, which shows the potential of using deep learning technique for hypervolume approximation.

Hypervolume-Optimal $μ$-Distributions on Line/Plane-based Pareto Fronts in Three Dimensions

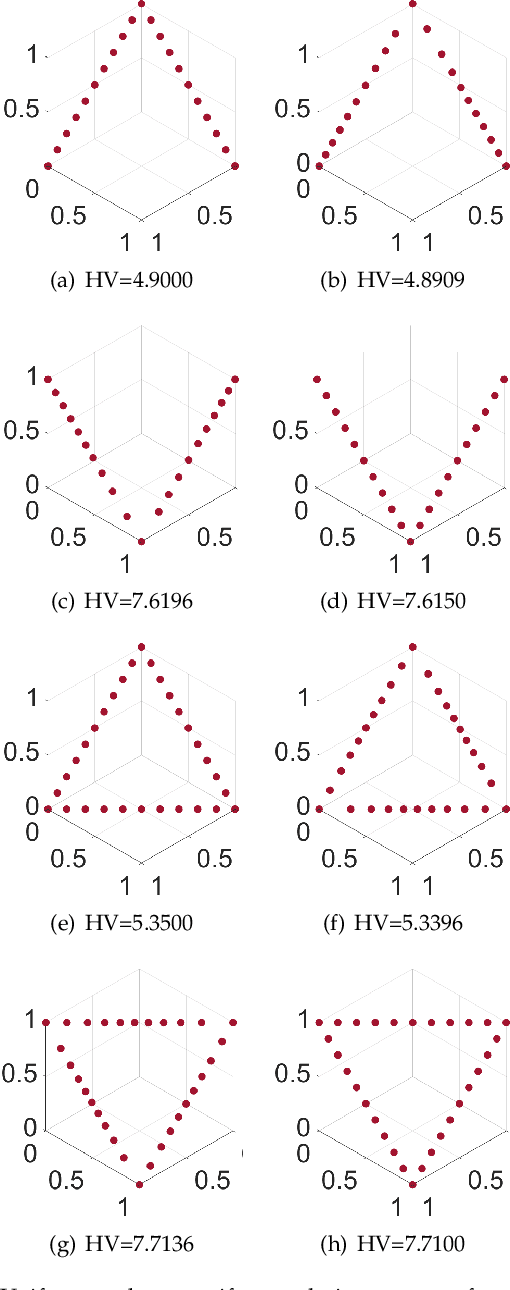
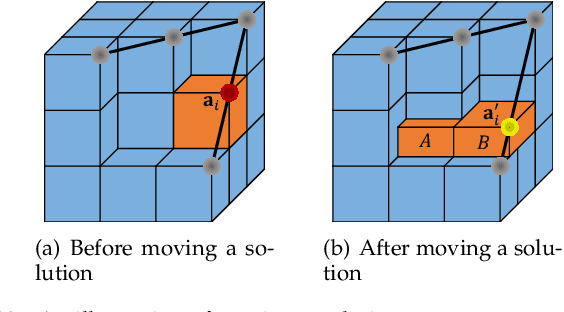
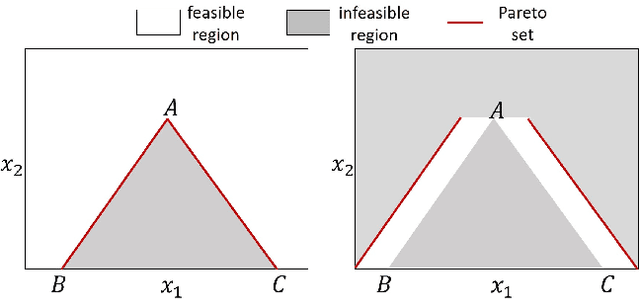
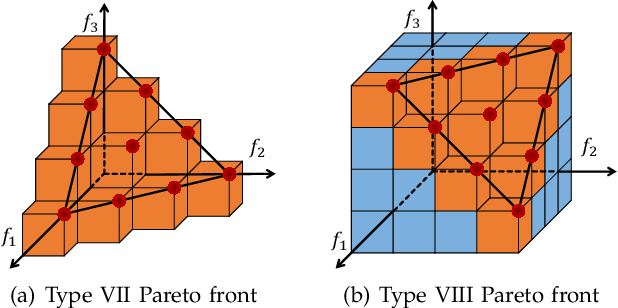
Hypervolume is widely used in the evolutionary multi-objective optimization (EMO) field to evaluate the quality of a solution set. For a solution set with $\mu$ solutions on a Pareto front, a larger hypervolume means a better solution set. Investigating the distribution of the solution set with the largest hypervolume is an important topic in EMO, which is the so-called hypervolume optimal $\mu$-distribution. Theoretical results have shown that the $\mu$ solutions are uniformly distributed on a linear Pareto front in two dimensions. However, the $\mu$ solutions are not always uniformly distributed on a single-line Pareto front in three dimensions. They are only uniform when the single-line Pareto front has one constant objective. In this paper, we further investigate the hypervolume optimal $\mu$-distribution in three dimensions. We consider the line- and plane-based Pareto fronts. For the line-based Pareto fronts, we extend the single-line Pareto front to two-line and three-line Pareto fronts, where each line has one constant objective. For the plane-based Pareto fronts, the linear triangular and inverted triangular Pareto fronts are considered. First, we show that the $\mu$ solutions are not always uniformly distributed on the line-based Pareto fronts. The uniformity depends on how the lines are combined. Then, we show that a uniform solution set on the plane-based Pareto front is not always optimal for hypervolume maximization. It is locally optimal with respect to a $(\mu+1)$ selection scheme. Our results can help researchers in the community to better understand and utilize the hypervolume indicator.