NeuraChip: Accelerating GNN Computations with a Hash-based Decoupled Spatial Accelerator

Graph Neural Networks (GNNs) are emerging as a formidable tool for processing non-euclidean data across various domains, ranging from social network analysis to bioinformatics. Despite their effectiveness, their adoption has not been pervasive because of scalability challenges associated with large-scale graph datasets, particularly when leveraging message passing. To tackle these challenges, we introduce NeuraChip, a novel GNN spatial accelerator based on Gustavson's algorithm. NeuraChip decouples the multiplication and addition computations in sparse matrix multiplication. This separation allows for independent exploitation of their unique data dependencies, facilitating efficient resource allocation. We introduce a rolling eviction strategy to mitigate data idling in on-chip memory as well as address the prevalent issue of memory bloat in sparse graph computations. Furthermore, the compute resource load balancing is achieved through a dynamic reseeding hash-based mapping, ensuring uniform utilization of computing resources agnostic of sparsity patterns. Finally, we present NeuraSim, an open-source, cycle-accurate, multi-threaded, modular simulator for comprehensive performance analysis. Overall, NeuraChip presents a significant improvement, yielding an average speedup of 22.1x over Intel's MKL, 17.1x over NVIDIA's cuSPARSE, 16.7x over AMD's hipSPARSE, and 1.5x over prior state-of-the-art SpGEMM accelerator and 1.3x over GNN accelerator. The source code for our open-sourced simulator and performance visualizer is publicly accessible on GitHub https://neurachip.us

MaxK-GNN: Towards Theoretical Speed Limits for Accelerating Graph Neural Networks Training

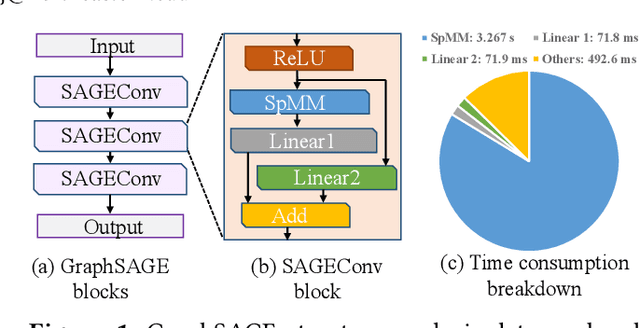
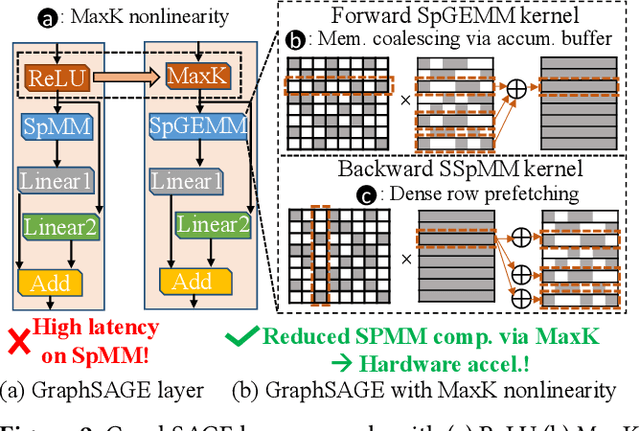
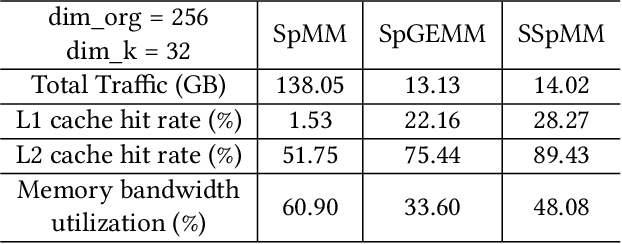
In the acceleration of deep neural network training, the GPU has become the mainstream platform. GPUs face substantial challenges on GNNs, such as workload imbalance and memory access irregularities, leading to underutilized hardware. Existing solutions such as PyG, DGL with cuSPARSE, and GNNAdvisor frameworks partially address these challenges but memory traffic is still significant. We argue that drastic performance improvements can only be achieved by the vertical optimization of algorithm and system innovations, rather than treating the speedup optimization as an "after-thought" (i.e., (i) given a GNN algorithm, designing an accelerator, or (ii) given hardware, mainly optimizing the GNN algorithm). In this paper, we present MaxK-GNN, an advanced high-performance GPU training system integrating algorithm and system innovation. (i) We introduce the MaxK nonlinearity and provide a theoretical analysis of MaxK nonlinearity as a universal approximator, and present the Compressed Balanced Sparse Row (CBSR) format, designed to store the data and index of the feature matrix after nonlinearity; (ii) We design a coalescing enhanced forward computation with row-wise product-based SpGEMM Kernel using CBSR for input feature matrix fetching and strategic placement of a sparse output accumulation buffer in shared memory; (iii) We develop an optimized backward computation with outer product-based and SSpMM Kernel. We conduct extensive evaluations of MaxK-GNN and report the end-to-end system run-time. Experiments show that MaxK-GNN system could approach the theoretical speedup limit according to Amdahl's law. We achieve comparable accuracy to SOTA GNNs, but at a significantly increased speed: 3.22/4.24 times speedup (vs. theoretical limits, 5.52/7.27 times) on Reddit compared to DGL and GNNAdvisor implementations.

Enabling Accelerators for Graph Computing

The advent of Graph Neural Networks (GNNs) has revolutionized the field of machine learning, offering a novel paradigm for learning on graph-structured data. Unlike traditional neural networks, GNNs are capable of capturing complex relationships and dependencies inherent in graph data, making them particularly suited for a wide range of applications including social network analysis, molecular chemistry, and network security. The impact of GNNs in these domains is profound, enabling more accurate models and predictions, and thereby contributing significantly to advancements in these fields. GNNs, with their unique structure and operation, present new computational challenges compared to conventional neural networks. This requires comprehensive benchmarking and a thorough characterization of GNNs to obtain insight into their computational requirements and to identify potential performance bottlenecks. In this thesis, we aim to develop a better understanding of how GNNs interact with the underlying hardware and will leverage this knowledge as we design specialized accelerators and develop new optimizations, leading to more efficient and faster GNN computations. Synthesizing these insights and optimizations, we design a state-of-the-art hardware accelerator capable of efficiently handling various GNN workloads. Our accelerator architecture is built on our characterization of GNN computational demands, providing clear motivation for our approach. Furthermore, we extend our exploration to emerging GNN workloads in the domain of graph neural networks. This exploration into novel models underlines our comprehensive approach, as we strive to enable accelerators that are not just performant, but also versatile, able to adapt to the evolving landscape of graph computing.

SMASH: Sparse Matrix Atomic Scratchpad Hashing

Sparse matrices, more specifically SpGEMM kernels, are commonly found in a wide range of applications, spanning graph-based path-finding to machine learning algorithms (e.g., neural networks). A particular challenge in implementing SpGEMM kernels has been the pressure placed on DRAM memory. One approach to tackle this problem is to use an inner product method for the SpGEMM kernel implementation. While the inner product produces fewer intermediate results, it can end up saturating the memory bandwidth, given the high number of redundant fetches of the input matrix elements. Using an outer product-based SpGEMM kernel can reduce redundant fetches, but at the cost of increased overhead due to extra computation and memory accesses for producing/managing partial products. In this thesis, we introduce a novel SpGEMM kernel implementation based on the row-wise product approach. We leverage atomic instructions to merge intermediate partial products as they are generated. The use of atomic instructions eliminates the need to create partial product matrices. To evaluate our row-wise product approach, we map an optimized SpGEMM kernel to a custom accelerator designed to accelerate graph-based applications. The targeted accelerator is an experimental system named PIUMA, being developed by Intel. PIUMA provides several attractive features, including fast context switching, user-configurable caches, globally addressable memory, non-coherent caches, and asynchronous pipelines. We tailor our SpGEMM kernel to exploit many of the features of the PIUMA fabric. This thesis compares our SpGEMM implementation against prior solutions, all mapped to the PIUMA framework. We briefly describe some of the PIUMA architecture features and then delve into the details of our optimized SpGEMM kernel. Our SpGEMM kernel can achieve 9.4x speedup as compared to competing approaches.