Hardness of Maximum Likelihood Learning of DPPs

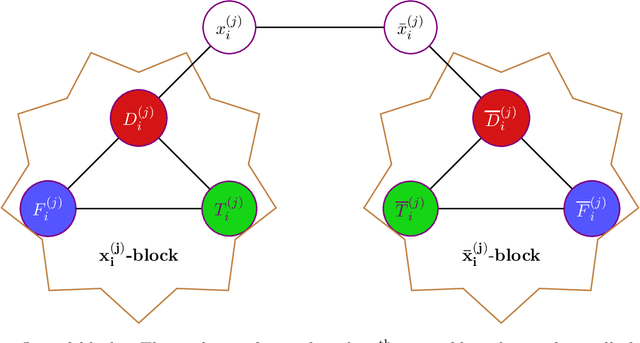
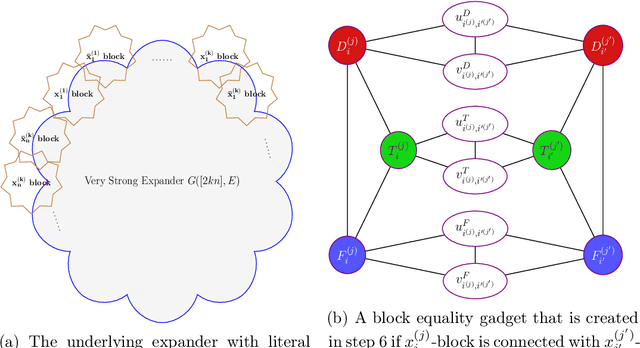
Determinantal Point Processes (DPPs) are a widely used probabilistic model for negatively correlated sets. DPPs have been successfully employed in Machine Learning applications to select a diverse, yet representative subset of data. In seminal work on DPPs in Machine Learning, Kulesza conjectured in his PhD Thesis (2011) that the problem of finding a maximum likelihood DPP model for a given data set is NP-complete. In this work we prove Kulesza's conjecture. In fact, we prove the following stronger hardness of approximation result: even computing a $\left(1-O(\frac{1}{\log^9{N}})\right)$-approximation to the maximum log-likelihood of a DPP on a ground set of $N$ elements is NP-complete. At the same time, we also obtain the first polynomial-time algorithm that achieves a nontrivial worst-case approximation to the optimal log-likelihood: the approximation factor is $\frac{1}{(1+o(1))\log{m}}$ unconditionally (for data sets that consist of $m$ subsets), and can be improved to $1-\frac{1+o(1)}{\log N}$ if all $N$ elements appear in a $O(1/N)$-fraction of the subsets. In terms of techniques, we reduce approximating the maximum log-likelihood of DPPs on a data set to solving a gap instance of a "vector coloring" problem on a hypergraph. Such a hypergraph is built on a bounded-degree graph construction of Bogdanov, Obata and Trevisan (FOCS 2002), and is further enhanced by the strong expanders of Alon and Capalbo (FOCS 2007) to serve our purposes.

List Learning with Attribute Noise

We introduce and study the model of list learning with attribute noise. Learning with attribute noise was introduced by Shackelford and Volper (COLT 1988) as a variant of PAC learning, in which the algorithm has access to noisy examples and uncorrupted labels, and the goal is to recover an accurate hypothesis. Sloan (COLT 1988) and Goldman and Sloan (Algorithmica 1995) discovered information-theoretic limits to learning in this model, which have impeded further progress. In this article we extend the model to that of list learning, drawing inspiration from the list-decoding model in coding theory, and its recent variant studied in the context of learning. On the positive side, we show that sparse conjunctions can be efficiently list learned under some assumptions on the underlying ground-truth distribution. On the negative side, our results show that even in the list-learning model, efficient learning of parities and majorities is not possible regardless of the representation used.

Testing $k$-Monotonicity

A Boolean $k$-monotone function defined over a finite poset domain ${\cal D}$ alternates between the values $0$ and $1$ at most $k$ times on any ascending chain in ${\cal D}$. Therefore, $k$-monotone functions are natural generalizations of the classical monotone functions, which are the $1$-monotone functions. Motivated by the recent interest in $k$-monotone functions in the context of circuit complexity and learning theory, and by the central role that monotonicity testing plays in the context of property testing, we initiate a systematic study of $k$-monotone functions, in the property testing model. In this model, the goal is to distinguish functions that are $k$-monotone (or are close to being $k$-monotone) from functions that are far from being $k$-monotone. Our results include the following: - We demonstrate a separation between testing $k$-monotonicity and testing monotonicity, on the hypercube domain $\{0,1\}^d$, for $k\geq 3$; - We demonstrate a separation between testing and learning on $\{0,1\}^d$, for $k=\omega(\log d)$: testing $k$-monotonicity can be performed with $2^{O(\sqrt d \cdot \log d\cdot \log{1/\varepsilon})}$ queries, while learning $k$-monotone functions requires $2^{\Omega(k\cdot \sqrt d\cdot{1/\varepsilon})}$ queries (Blais et al. (RANDOM 2015)). - We present a tolerant test for functions $f\colon[n]^d\to \{0,1\}$ with complexity independent of $n$, which makes progress on a problem left open by Berman et al. (STOC 2014). Our techniques exploit the testing-by-learning paradigm, use novel applications of Fourier analysis on the grid $[n]^d$, and draw connections to distribution testing techniques.

Approximate resilience, monotonicity, and the complexity of agnostic learning

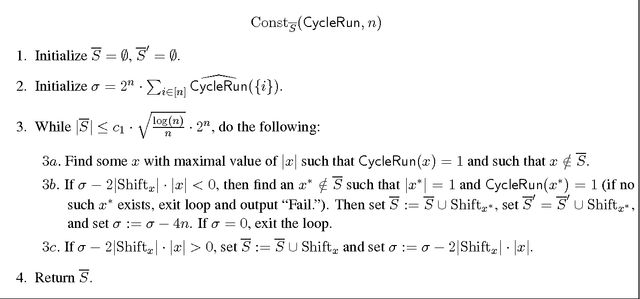
A function $f$ is $d$-resilient if all its Fourier coefficients of degree at most $d$ are zero, i.e., $f$ is uncorrelated with all low-degree parities. We study the notion of $\mathit{approximate}$ $\mathit{resilience}$ of Boolean functions, where we say that $f$ is $\alpha$-approximately $d$-resilient if $f$ is $\alpha$-close to a $[-1,1]$-valued $d$-resilient function in $\ell_1$ distance. We show that approximate resilience essentially characterizes the complexity of agnostic learning of a concept class $C$ over the uniform distribution. Roughly speaking, if all functions in a class $C$ are far from being $d$-resilient then $C$ can be learned agnostically in time $n^{O(d)}$ and conversely, if $C$ contains a function close to being $d$-resilient then agnostic learning of $C$ in the statistical query (SQ) framework of Kearns has complexity of at least $n^{\Omega(d)}$. This characterization is based on the duality between $\ell_1$ approximation by degree-$d$ polynomials and approximate $d$-resilience that we establish. In particular, it implies that $\ell_1$ approximation by low-degree polynomials, known to be sufficient for agnostic learning over product distributions, is in fact necessary. Focusing on monotone Boolean functions, we exhibit the existence of near-optimal $\alpha$-approximately $\widetilde{\Omega}(\alpha\sqrt{n})$-resilient monotone functions for all $\alpha>0$. Prior to our work, it was conceivable even that every monotone function is $\Omega(1)$-far from any $1$-resilient function. Furthermore, we construct simple, explicit monotone functions based on ${\sf Tribes}$ and ${\sf CycleRun}$ that are close to highly resilient functions. Our constructions are based on a fairly general resilience analysis and amplification. These structural results, together with the characterization, imply nearly optimal lower bounds for agnostic learning of monotone juntas.