Hardness of Maximum Likelihood Learning of DPPs
Paper and Code
May 26, 2022
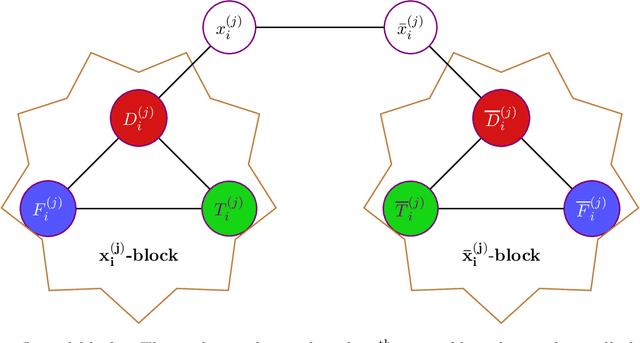

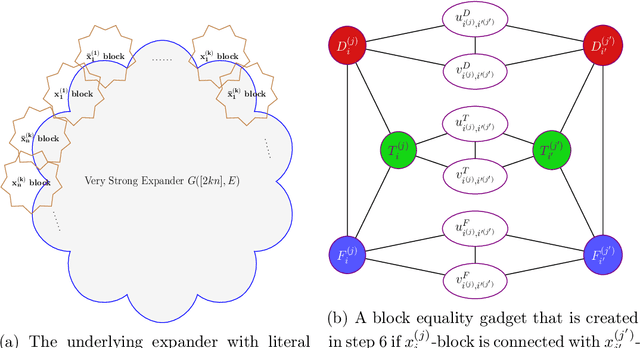
Determinantal Point Processes (DPPs) are a widely used probabilistic model for negatively correlated sets. DPPs have been successfully employed in Machine Learning applications to select a diverse, yet representative subset of data. In seminal work on DPPs in Machine Learning, Kulesza conjectured in his PhD Thesis (2011) that the problem of finding a maximum likelihood DPP model for a given data set is NP-complete. In this work we prove Kulesza's conjecture. In fact, we prove the following stronger hardness of approximation result: even computing a $\left(1-O(\frac{1}{\log^9{N}})\right)$-approximation to the maximum log-likelihood of a DPP on a ground set of $N$ elements is NP-complete. At the same time, we also obtain the first polynomial-time algorithm that achieves a nontrivial worst-case approximation to the optimal log-likelihood: the approximation factor is $\frac{1}{(1+o(1))\log{m}}$ unconditionally (for data sets that consist of $m$ subsets), and can be improved to $1-\frac{1+o(1)}{\log N}$ if all $N$ elements appear in a $O(1/N)$-fraction of the subsets. In terms of techniques, we reduce approximating the maximum log-likelihood of DPPs on a data set to solving a gap instance of a "vector coloring" problem on a hypergraph. Such a hypergraph is built on a bounded-degree graph construction of Bogdanov, Obata and Trevisan (FOCS 2002), and is further enhanced by the strong expanders of Alon and Capalbo (FOCS 2007) to serve our purposes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge