A Simple Learning-Augmented Algorithm for Online Packing with Concave Objectives

Learning-augmented algorithms has been extensively studied recently in the computer-science community, due to the potential of using machine learning predictions in order to improve the performance of algorithms. Predictions are especially useful for online algorithms making irrevocable decisions without knowledge of the future. Such learning-augmented algorithms aim to overcome the limitations of classical online algorithms when the predictions are accurate, and still perform comparably when the predictions are inaccurate. A common approach is to adapt existing online algorithms to the particular advice notion employed, which often involves understanding previous sophisticated algorithms and their analyses. However, ideally, one would simply use previous online solutions in a black-box fashion, without much loss in the approximation guarantees. Such clean solutions that avoid opening up black-boxes are often rare, and may be even missed the first time around. For example, Grigorescu et al. (NeurIPS 22) proposed a learning-augmented algorithms for online covering linear programs, but it later turned out that their results can be subsumed by a natural approach that switches between the advice and an online algorithm given as a black-box, as noted in their paper. In this work, we introduce and analyze a simple learning-augmented algorithm for online packing problems with linear constraints and concave objectives. We exhibit several direct applications of our framework including online packing linear programming, knapsack, resource management benefit, throughput maximization, and network utility maximization. We further raise the problem of understanding necessary and sufficient conditions for when such simple black-box solutions may be optimal. We believe this is an important direction of research that would unify many ad-hoc approaches from the literature.

Learning-Augmented Algorithms for Online Linear and Semidefinite Programming

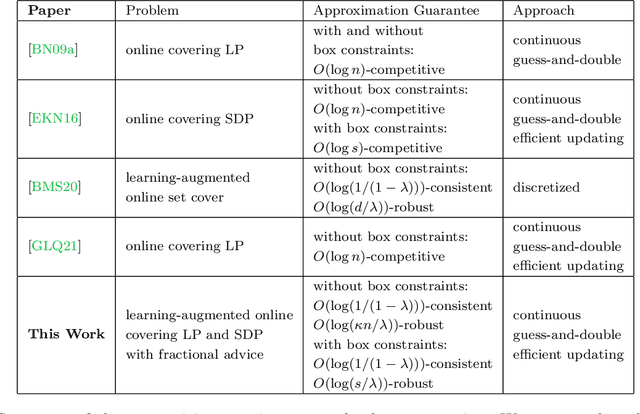
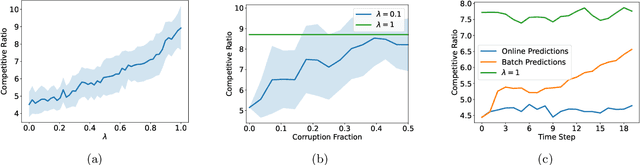
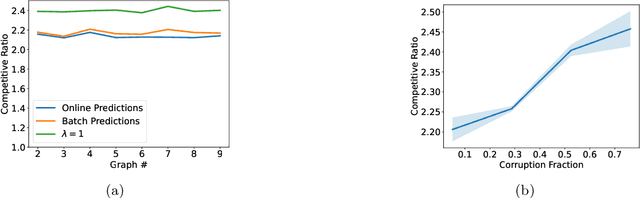
Semidefinite programming (SDP) is a unifying framework that generalizes both linear programming and quadratically-constrained quadratic programming, while also yielding efficient solvers, both in theory and in practice. However, there exist known impossibility results for approximating the optimal solution when constraints for covering SDPs arrive in an online fashion. In this paper, we study online covering linear and semidefinite programs in which the algorithm is augmented with advice from a possibly erroneous predictor. We show that if the predictor is accurate, we can efficiently bypass these impossibility results and achieve a constant-factor approximation to the optimal solution, i.e., consistency. On the other hand, if the predictor is inaccurate, under some technical conditions, we achieve results that match both the classical optimal upper bounds and the tight lower bounds up to constant factors, i.e., robustness. More broadly, we introduce a framework that extends both (1) the online set cover problem augmented with machine-learning predictors, studied by Bamas, Maggiori, and Svensson (NeurIPS 2020), and (2) the online covering SDP problem, initiated by Elad, Kale, and Naor (ICALP 2016). Specifically, we obtain general online learning-augmented algorithms for covering linear programs with fractional advice and constraints, and initiate the study of learning-augmented algorithms for covering SDP problems. Our techniques are based on the primal-dual framework of Buchbinder and Naor (Mathematics of Operations Research, 34, 2009) and can be further adjusted to handle constraints where the variables lie in a bounded region, i.e., box constraints.

Hardness of Maximum Likelihood Learning of DPPs

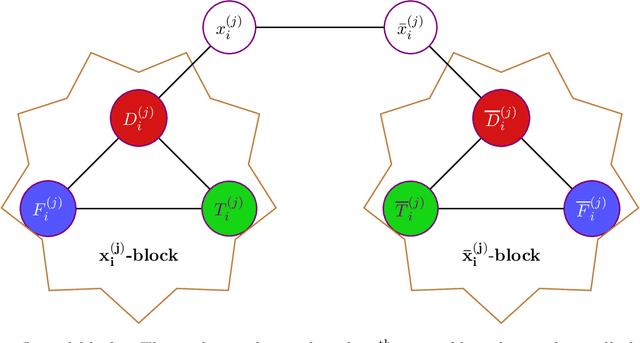
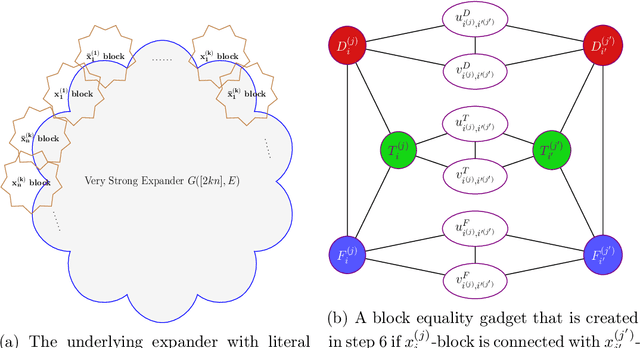
Determinantal Point Processes (DPPs) are a widely used probabilistic model for negatively correlated sets. DPPs have been successfully employed in Machine Learning applications to select a diverse, yet representative subset of data. In seminal work on DPPs in Machine Learning, Kulesza conjectured in his PhD Thesis (2011) that the problem of finding a maximum likelihood DPP model for a given data set is NP-complete. In this work we prove Kulesza's conjecture. In fact, we prove the following stronger hardness of approximation result: even computing a $\left(1-O(\frac{1}{\log^9{N}})\right)$-approximation to the maximum log-likelihood of a DPP on a ground set of $N$ elements is NP-complete. At the same time, we also obtain the first polynomial-time algorithm that achieves a nontrivial worst-case approximation to the optimal log-likelihood: the approximation factor is $\frac{1}{(1+o(1))\log{m}}$ unconditionally (for data sets that consist of $m$ subsets), and can be improved to $1-\frac{1+o(1)}{\log N}$ if all $N$ elements appear in a $O(1/N)$-fraction of the subsets. In terms of techniques, we reduce approximating the maximum log-likelihood of DPPs on a data set to solving a gap instance of a "vector coloring" problem on a hypergraph. Such a hypergraph is built on a bounded-degree graph construction of Bogdanov, Obata and Trevisan (FOCS 2002), and is further enhanced by the strong expanders of Alon and Capalbo (FOCS 2007) to serve our purposes.

Differentially-Private Sublinear-Time Clustering

Clustering is an essential primitive in unsupervised machine learning. We bring forth the problem of sublinear-time differentially-private clustering as a natural and well-motivated direction of research. We combine the $k$-means and $k$-median sublinear-time results of Mishra et al. (SODA, 2001) and of Czumaj and Sohler (Rand. Struct. and Algorithms, 2007) with recent results on private clustering of Balcan et al. (ICML 2017), Gupta et al. (SODA, 2010) and Ghazi et al. (NeurIPS, 2020) to obtain sublinear-time private $k$-means and $k$-median algorithms via subsampling. We also investigate the privacy benefits of subsampling for group privacy.

List Learning with Attribute Noise

We introduce and study the model of list learning with attribute noise. Learning with attribute noise was introduced by Shackelford and Volper (COLT 1988) as a variant of PAC learning, in which the algorithm has access to noisy examples and uncorrupted labels, and the goal is to recover an accurate hypothesis. Sloan (COLT 1988) and Goldman and Sloan (Algorithmica 1995) discovered information-theoretic limits to learning in this model, which have impeded further progress. In this article we extend the model to that of list learning, drawing inspiration from the list-decoding model in coding theory, and its recent variant studied in the context of learning. On the positive side, we show that sparse conjunctions can be efficiently list learned under some assumptions on the underlying ground-truth distribution. On the negative side, our results show that even in the list-learning model, efficient learning of parities and majorities is not possible regardless of the representation used.

Testing $k$-Monotonicity

A Boolean $k$-monotone function defined over a finite poset domain ${\cal D}$ alternates between the values $0$ and $1$ at most $k$ times on any ascending chain in ${\cal D}$. Therefore, $k$-monotone functions are natural generalizations of the classical monotone functions, which are the $1$-monotone functions. Motivated by the recent interest in $k$-monotone functions in the context of circuit complexity and learning theory, and by the central role that monotonicity testing plays in the context of property testing, we initiate a systematic study of $k$-monotone functions, in the property testing model. In this model, the goal is to distinguish functions that are $k$-monotone (or are close to being $k$-monotone) from functions that are far from being $k$-monotone. Our results include the following: - We demonstrate a separation between testing $k$-monotonicity and testing monotonicity, on the hypercube domain $\{0,1\}^d$, for $k\geq 3$; - We demonstrate a separation between testing and learning on $\{0,1\}^d$, for $k=\omega(\log d)$: testing $k$-monotonicity can be performed with $2^{O(\sqrt d \cdot \log d\cdot \log{1/\varepsilon})}$ queries, while learning $k$-monotone functions requires $2^{\Omega(k\cdot \sqrt d\cdot{1/\varepsilon})}$ queries (Blais et al. (RANDOM 2015)). - We present a tolerant test for functions $f\colon[n]^d\to \{0,1\}$ with complexity independent of $n$, which makes progress on a problem left open by Berman et al. (STOC 2014). Our techniques exploit the testing-by-learning paradigm, use novel applications of Fourier analysis on the grid $[n]^d$, and draw connections to distribution testing techniques.