A Simple Learning-Augmented Algorithm for Online Packing with Concave Objectives

Learning-augmented algorithms has been extensively studied recently in the computer-science community, due to the potential of using machine learning predictions in order to improve the performance of algorithms. Predictions are especially useful for online algorithms making irrevocable decisions without knowledge of the future. Such learning-augmented algorithms aim to overcome the limitations of classical online algorithms when the predictions are accurate, and still perform comparably when the predictions are inaccurate. A common approach is to adapt existing online algorithms to the particular advice notion employed, which often involves understanding previous sophisticated algorithms and their analyses. However, ideally, one would simply use previous online solutions in a black-box fashion, without much loss in the approximation guarantees. Such clean solutions that avoid opening up black-boxes are often rare, and may be even missed the first time around. For example, Grigorescu et al. (NeurIPS 22) proposed a learning-augmented algorithms for online covering linear programs, but it later turned out that their results can be subsumed by a natural approach that switches between the advice and an online algorithm given as a black-box, as noted in their paper. In this work, we introduce and analyze a simple learning-augmented algorithm for online packing problems with linear constraints and concave objectives. We exhibit several direct applications of our framework including online packing linear programming, knapsack, resource management benefit, throughput maximization, and network utility maximization. We further raise the problem of understanding necessary and sufficient conditions for when such simple black-box solutions may be optimal. We believe this is an important direction of research that would unify many ad-hoc approaches from the literature.

Optimality in Mean Estimation: Beyond Worst-Case, Beyond Sub-Gaussian, and Beyond $1+α$ Moments

There is growing interest in improving our algorithmic understanding of fundamental statistical problems such as mean estimation, driven by the goal of understanding the limits of what we can extract from valuable data. The state of the art results for mean estimation in $\mathbb{R}$ are 1) the optimal sub-Gaussian mean estimator by [LV22], with the tight sub-Gaussian constant for all distributions with finite but unknown variance, and 2) the analysis of the median-of-means algorithm by [BCL13] and a lower bound by [DLLO16], characterizing the big-O optimal errors for distributions for which only a $1+\alpha$ moment exists for $\alpha \in (0,1)$. Both results, however, are optimal only in the worst case. We initiate the fine-grained study of the mean estimation problem: Can algorithms leverage useful features of the input distribution to beat the sub-Gaussian rate, without explicit knowledge of such features? We resolve this question with an unexpectedly nuanced answer: "Yes in limited regimes, but in general no". For any distribution $p$ with a finite mean, we construct a distribution $q$ whose mean is well-separated from $p$'s, yet $p$ and $q$ are not distinguishable with high probability, and $q$ further preserves $p$'s moments up to constants. The main consequence is that no reasonable estimator can asymptotically achieve better than the sub-Gaussian error rate for any distribution, matching the worst-case result of [LV22]. More generally, we introduce a new definitional framework to analyze the fine-grained optimality of algorithms, which we call "neighborhood optimality", interpolating between the unattainably strong "instance optimality" and the trivially weak "admissibility" definitions. Applying the new framework, we show that median-of-means is neighborhood optimal, up to constant factors. It is open to find a neighborhood-optimal estimator without constant factor slackness.

Learning-Augmented Algorithms for Online Linear and Semidefinite Programming

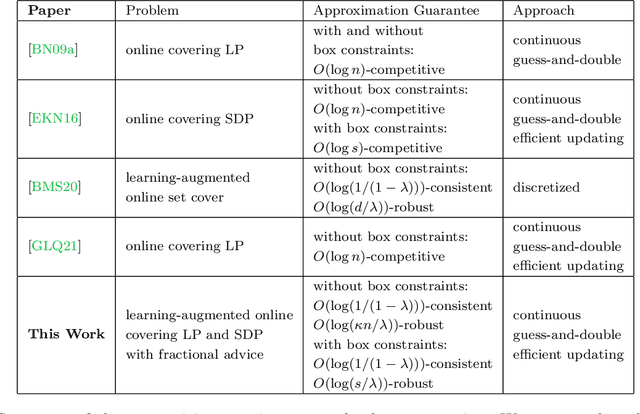
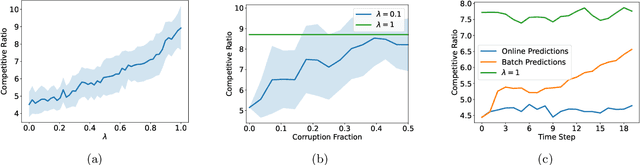
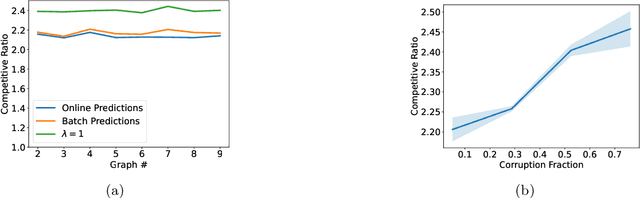
Semidefinite programming (SDP) is a unifying framework that generalizes both linear programming and quadratically-constrained quadratic programming, while also yielding efficient solvers, both in theory and in practice. However, there exist known impossibility results for approximating the optimal solution when constraints for covering SDPs arrive in an online fashion. In this paper, we study online covering linear and semidefinite programs in which the algorithm is augmented with advice from a possibly erroneous predictor. We show that if the predictor is accurate, we can efficiently bypass these impossibility results and achieve a constant-factor approximation to the optimal solution, i.e., consistency. On the other hand, if the predictor is inaccurate, under some technical conditions, we achieve results that match both the classical optimal upper bounds and the tight lower bounds up to constant factors, i.e., robustness. More broadly, we introduce a framework that extends both (1) the online set cover problem augmented with machine-learning predictors, studied by Bamas, Maggiori, and Svensson (NeurIPS 2020), and (2) the online covering SDP problem, initiated by Elad, Kale, and Naor (ICALP 2016). Specifically, we obtain general online learning-augmented algorithms for covering linear programs with fractional advice and constraints, and initiate the study of learning-augmented algorithms for covering SDP problems. Our techniques are based on the primal-dual framework of Buchbinder and Naor (Mathematics of Operations Research, 34, 2009) and can be further adjusted to handle constraints where the variables lie in a bounded region, i.e., box constraints.