Depth Separations in Neural Networks: Separating the Dimension from the Accuracy

We prove an exponential separation between depth 2 and depth 3 neural networks, when approximating an $\mathcal{O}(1)$-Lipschitz target function to constant accuracy, with respect to a distribution with support in $[0,1]^{d}$, assuming exponentially bounded weights. This addresses an open problem posed in \citet{safran2019depth}, and proves that the curse of dimensionality manifests in depth 2 approximation, even in cases where the target function can be represented efficiently using depth 3. Previously, lower bounds that were used to separate depth 2 from depth 3 required that at least one of the Lipschitz parameter, target accuracy or (some measure of) the size of the domain of approximation scale polynomially with the input dimension, whereas we fix the former two and restrict our domain to the unit hypercube. Our lower bound holds for a wide variety of activation functions, and is based on a novel application of an average- to worst-case random self-reducibility argument, to reduce the problem to threshold circuits lower bounds.

Optimality in Mean Estimation: Beyond Worst-Case, Beyond Sub-Gaussian, and Beyond $1+α$ Moments

There is growing interest in improving our algorithmic understanding of fundamental statistical problems such as mean estimation, driven by the goal of understanding the limits of what we can extract from valuable data. The state of the art results for mean estimation in $\mathbb{R}$ are 1) the optimal sub-Gaussian mean estimator by [LV22], with the tight sub-Gaussian constant for all distributions with finite but unknown variance, and 2) the analysis of the median-of-means algorithm by [BCL13] and a lower bound by [DLLO16], characterizing the big-O optimal errors for distributions for which only a $1+\alpha$ moment exists for $\alpha \in (0,1)$. Both results, however, are optimal only in the worst case. We initiate the fine-grained study of the mean estimation problem: Can algorithms leverage useful features of the input distribution to beat the sub-Gaussian rate, without explicit knowledge of such features? We resolve this question with an unexpectedly nuanced answer: "Yes in limited regimes, but in general no". For any distribution $p$ with a finite mean, we construct a distribution $q$ whose mean is well-separated from $p$'s, yet $p$ and $q$ are not distinguishable with high probability, and $q$ further preserves $p$'s moments up to constants. The main consequence is that no reasonable estimator can asymptotically achieve better than the sub-Gaussian error rate for any distribution, matching the worst-case result of [LV22]. More generally, we introduce a new definitional framework to analyze the fine-grained optimality of algorithms, which we call "neighborhood optimality", interpolating between the unattainably strong "instance optimality" and the trivially weak "admissibility" definitions. Applying the new framework, we show that median-of-means is neighborhood optimal, up to constant factors. It is open to find a neighborhood-optimal estimator without constant factor slackness.

How Many Neurons Does it Take to Approximate the Maximum?

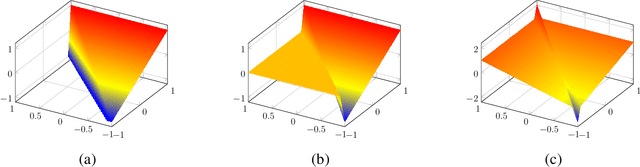
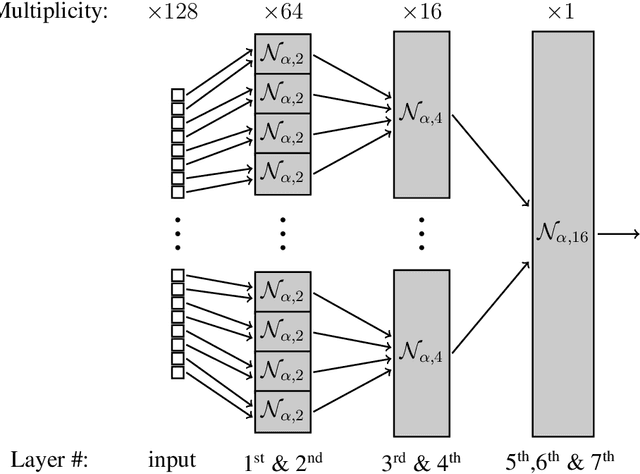
We study the size of a neural network needed to approximate the maximum function over $d$ inputs, in the most basic setting of approximating with respect to the $L_2$ norm, for continuous distributions, for a network that uses ReLU activations. We provide new lower and upper bounds on the width required for approximation across various depths. Our results establish new depth separations between depth 2 and 3, and depth 3 and 5 networks, as well as providing a depth $\mathcal{O}(\log(\log(d)))$ and width $\mathcal{O}(d)$ construction which approximates the maximum function, significantly improving upon the depth requirements of the best previously known bounds for networks with linearly-bounded width. Our depth separation results are facilitated by a new lower bound for depth 2 networks approximating the maximum function over the uniform distribution, assuming an exponential upper bound on the size of the weights. Furthermore, we are able to use this depth 2 lower bound to provide tight bounds on the number of neurons needed to approximate the maximum by a depth 3 network. Our lower bounds are of potentially broad interest as they apply to the widely studied and used \emph{max} function, in contrast to many previous results that base their bounds on specially constructed or pathological functions and distributions.

Finite-Sample Maximum Likelihood Estimation of Location

We consider 1-dimensional location estimation, where we estimate a parameter $\lambda$ from $n$ samples $\lambda + \eta_i$, with each $\eta_i$ drawn i.i.d. from a known distribution $f$. For fixed $f$ the maximum-likelihood estimate (MLE) is well-known to be optimal in the limit as $n \to \infty$: it is asymptotically normal with variance matching the Cram\'er-Rao lower bound of $\frac{1}{n\mathcal{I}}$, where $\mathcal{I}$ is the Fisher information of $f$. However, this bound does not hold for finite $n$, or when $f$ varies with $n$. We show for arbitrary $f$ and $n$ that one can recover a similar theory based on the Fisher information of a smoothed version of $f$, where the smoothing radius decays with $n$.

Optimal Sub-Gaussian Mean Estimation in $\mathbb{R}$

We revisit the problem of estimating the mean of a real-valued distribution, presenting a novel estimator with sub-Gaussian convergence: intuitively, "our estimator, on any distribution, is as accurate as the sample mean is for the Gaussian distribution of matching variance." Crucially, in contrast to prior works, our estimator does not require prior knowledge of the variance, and works across the entire gamut of distributions with bounded variance, including those without any higher moments. Parameterized by the sample size $n$, the failure probability $\delta$, and the variance $\sigma^2$, our estimator is accurate to within $\sigma\cdot(1+o(1))\sqrt{\frac{2\log\frac{1}{\delta}}{n}}$, tight up to the $1+o(1)$ factor. Our estimator construction and analysis gives a framework generalizable to other problems, tightly analyzing a sum of dependent random variables by viewing the sum implicitly as a 2-parameter $\psi$-estimator, and constructing bounds using mathematical programming and duality techniques.

How bad is worst-case data if you know where it comes from?

We introduce a framework for studying how distributional assumptions on the process by which data is partitioned into a training and test set can be leveraged to provide accurate estimation or learning algorithms, even for worst-case datasets. We consider a setting of $n$ datapoints, $x_1,\ldots,x_n$, together with a specified distribution, $P$, over partitions of these datapoints into a training set, test set, and irrelevant set. An algorithm takes as input a description of $P$ (or sample access), the indices of the test and training sets, and the datapoints in the training set, and returns a model or estimate that will be evaluated on the datapoints in the test set. We evaluate an algorithm in terms of its worst-case expected performance: the expected performance over potential test/training sets, for worst-case datapoints, $x_1,\ldots,x_n.$ This framework is a departure from more typical distributional assumptions on the datapoints (e.g. that data is drawn independently, or according to an exchangeable process), and can model a number of natural data collection processes, including processes with dependencies such as "snowball sampling" and "chain sampling", and settings where test and training sets satisfy chronological constraints (e.g. the test instances were observed after the training instances). Within this framework, we consider the setting where datapoints are bounded real numbers, and the goal is to estimate the mean of the test set. We give an efficient algorithm that returns a weighted combination of the training set---whose weights depend on the distribution, $P$, and on the training and test set indices---and show that the worst-case expected error achieved by this algorithm is at most a multiplicative $\pi/2$ factor worse than the optimal of such algorithms. The algorithm, and its proof, leverage a surprising connection to the Grothendieck problem.

Uncertainty about Uncertainty: Near-Optimal Adaptive Algorithms for Estimating Binary Mixtures of Unknown Coins

Given a mixture between two populations of coins, "positive" coins that have (unknown and potentially different) probabilities of heads $\geq\frac{1}{2}+\Delta$ and negative coins with probabilities $\leq\frac{1}{2}-\Delta$, we consider the task of estimating the fraction $\rho$ of coins of each type to within additive error $\epsilon$. We introduce new techniques to show a fully-adaptive lower bound of $\Omega(\frac{\rho}{\epsilon^2\Delta^2})$ samples (for constant probability of success). We achieve almost-matching algorithmic performance of $O(\frac{\rho}{\epsilon^2\Delta^2}(1+\rho\log\frac{1}{\epsilon}))$ samples, which matches the lower bound except in the regime where $\rho=\omega(\frac{1}{\log 1/\epsilon})$. The fine-grained adaptive flavor of both our algorithm and lower bound contrasts with much previous work in distributional testing and learning.

Implicit regularization for deep neural networks driven by an Ornstein-Uhlenbeck like process

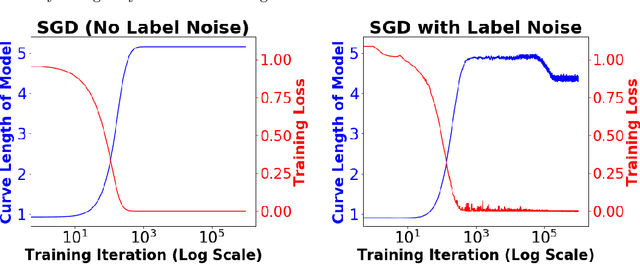
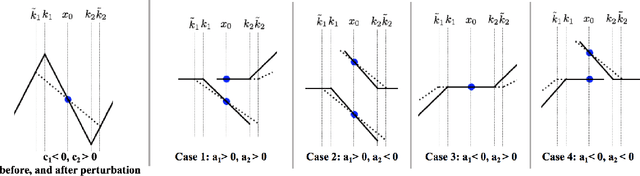
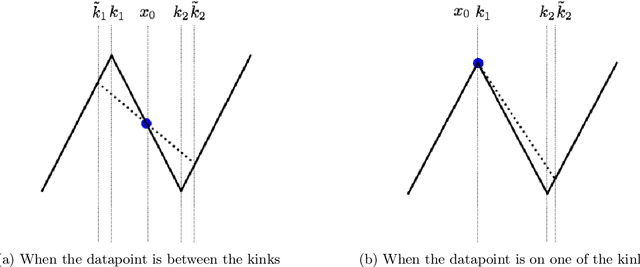
We consider deep networks, trained via stochastic gradient descent to minimize L2 loss, with the training labels perturbed by independent noise at each iteration. We characterize the behavior of the training dynamics near any parameter vector that achieves zero training error, in terms of an implicit regularization term corresponding to the sum over the data points, of the squared L2 norm of the gradient of the model with respect to the parameter vector, evaluated at each data point. We then leverage this general characterization, which holds for networks of any connectivity, width, depth, and choice of activation function, to show that for 2-layer ReLU networks of arbitrary width and L2 loss, when trained on one-dimensional labeled data $(x_1,y_1),\ldots,(x_n,y_n),$ the only stable solutions with zero training error correspond to functions that: 1) are linear over any set of three or more co-linear training points (i.e. the function has no extra "kinks"); and 2) change convexity the minimum number of times that is necessary to fit the training data. Additionally, for 2-layer networks of arbitrary width, with tanh or logistic activations, we show that when trained on a single $d$-dimensional point $(x,y)$ the only stable solutions correspond to networks where the activations of all hidden units at the datapoint, and all weights from the hidden units to the output, take at most two distinct values, or are zero. In this sense, we show that when trained on "simple" data, models corresponding to stable parameters are also "simple"; in short, despite fitting in an over-parameterized regime where the vast majority of expressible functions are complicated and badly behaved, stable parameters reached by training with noise express nearly the "simplest possible" hypothesis consistent with the data. These results shed light on the mystery of why deep networks generalize so well in practice.

Instance Optimal Learning

We consider the following basic learning task: given independent draws from an unknown distribution over a discrete support, output an approximation of the distribution that is as accurate as possible in $\ell_1$ distance (i.e. total variation or statistical distance). Perhaps surprisingly, it is often possible to "de-noise" the empirical distribution of the samples to return an approximation of the true distribution that is significantly more accurate than the empirical distribution, without relying on any prior assumptions on the distribution. We present an instance optimal learning algorithm which optimally performs this de-noising for every distribution for which such a de-noising is possible. More formally, given $n$ independent draws from a distribution $p$, our algorithm returns a labelled vector whose expected distance from $p$ is equal to the minimum possible expected error that could be obtained by any algorithm that knows the true unlabeled vector of probabilities of distribution $p$ and simply needs to assign labels, up to an additive subconstant term that is independent of $p$ and goes to zero as $n$ gets large. One conceptual implication of this result is that for large samples, Bayesian assumptions on the "shape" or bounds on the tail probabilities of a distribution over discrete support are not helpful for the task of learning the distribution. As a consequence of our techniques, we also show that given a set of $n$ samples from an arbitrary distribution, one can accurately estimate the expected number of distinct elements that will be observed in a sample of any size up to $n \log n$. This sort of extrapolation is practically relevant, particularly to domains such as genomics where it is important to understand how much more might be discovered given larger sample sizes, and we are optimistic that our approach is practically viable.

Optimal Algorithms for Testing Closeness of Discrete Distributions

We study the question of closeness testing for two discrete distributions. More precisely, given samples from two distributions $p$ and $q$ over an $n$-element set, we wish to distinguish whether $p=q$ versus $p$ is at least $\eps$-far from $q$, in either $\ell_1$ or $\ell_2$ distance. Batu et al. gave the first sub-linear time algorithms for these problems, which matched the lower bounds of Valiant up to a logarithmic factor in $n$, and a polynomial factor of $\eps.$ In this work, we present simple (and new) testers for both the $\ell_1$ and $\ell_2$ settings, with sample complexity that is information-theoretically optimal, to constant factors, both in the dependence on $n$, and the dependence on $\eps$; for the $\ell_1$ testing problem we establish that the sample complexity is $\Theta(\max\{n^{2/3}/\eps^{4/3}, n^{1/2}/\eps^2 \}).$