Near-Optimal Density Estimation in Near-Linear Time Using Variable-Width Histograms

Let $p$ be an unknown and arbitrary probability distribution over $[0,1)$. We consider the problem of {\em density estimation}, in which a learning algorithm is given i.i.d. draws from $p$ and must (with high probability) output a hypothesis distribution that is close to $p$. The main contribution of this paper is a highly efficient density estimation algorithm for learning using a variable-width histogram, i.e., a hypothesis distribution with a piecewise constant probability density function. In more detail, for any $k$ and $\epsilon$, we give an algorithm that makes $\tilde{O}(k/\epsilon^2)$ draws from $p$, runs in $\tilde{O}(k/\epsilon^2)$ time, and outputs a hypothesis distribution $h$ that is piecewise constant with $O(k \log^2(1/\epsilon))$ pieces. With high probability the hypothesis $h$ satisfies $d_{\mathrm{TV}}(p,h) \leq C \cdot \mathrm{opt}_k(p) + \epsilon$, where $d_{\mathrm{TV}}$ denotes the total variation distance (statistical distance), $C$ is a universal constant, and $\mathrm{opt}_k(p)$ is the smallest total variation distance between $p$ and any $k$-piecewise constant distribution. The sample size and running time of our algorithm are optimal up to logarithmic factors. The "approximation factor" $C$ in our result is inherent in the problem, as we prove that no algorithm with sample size bounded in terms of $k$ and $\epsilon$ can achieve $C<2$ regardless of what kind of hypothesis distribution it uses.

Optimal Algorithms for Testing Closeness of Discrete Distributions

We study the question of closeness testing for two discrete distributions. More precisely, given samples from two distributions $p$ and $q$ over an $n$-element set, we wish to distinguish whether $p=q$ versus $p$ is at least $\eps$-far from $q$, in either $\ell_1$ or $\ell_2$ distance. Batu et al. gave the first sub-linear time algorithms for these problems, which matched the lower bounds of Valiant up to a logarithmic factor in $n$, and a polynomial factor of $\eps.$ In this work, we present simple (and new) testers for both the $\ell_1$ and $\ell_2$ settings, with sample complexity that is information-theoretically optimal, to constant factors, both in the dependence on $n$, and the dependence on $\eps$; for the $\ell_1$ testing problem we establish that the sample complexity is $\Theta(\max\{n^{2/3}/\eps^{4/3}, n^{1/2}/\eps^2 \}).$

Efficient Density Estimation via Piecewise Polynomial Approximation

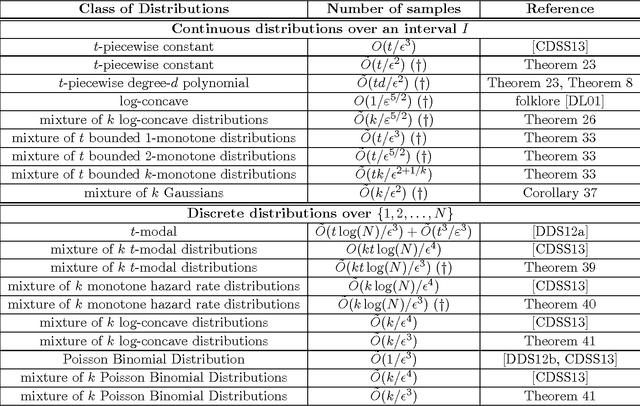
We give a highly efficient "semi-agnostic" algorithm for learning univariate probability distributions that are well approximated by piecewise polynomial density functions. Let $p$ be an arbitrary distribution over an interval $I$ which is $\tau$-close (in total variation distance) to an unknown probability distribution $q$ that is defined by an unknown partition of $I$ into $t$ intervals and $t$ unknown degree-$d$ polynomials specifying $q$ over each of the intervals. We give an algorithm that draws $\tilde{O}(t\new{(d+1)}/\eps^2)$ samples from $p$, runs in time $\poly(t,d,1/\eps)$, and with high probability outputs a piecewise polynomial hypothesis distribution $h$ that is $(O(\tau)+\eps)$-close (in total variation distance) to $p$. This sample complexity is essentially optimal; we show that even for $\tau=0$, any algorithm that learns an unknown $t$-piecewise degree-$d$ probability distribution over $I$ to accuracy $\eps$ must use $\Omega({\frac {t(d+1)} {\poly(1 + \log(d+1))}} \cdot {\frac 1 {\eps^2}})$ samples from the distribution, regardless of its running time. Our algorithm combines tools from approximation theory, uniform convergence, linear programming, and dynamic programming. We apply this general algorithm to obtain a wide range of results for many natural problems in density estimation over both continuous and discrete domains. These include state-of-the-art results for learning mixtures of log-concave distributions; mixtures of $t$-modal distributions; mixtures of Monotone Hazard Rate distributions; mixtures of Poisson Binomial Distributions; mixtures of Gaussians; and mixtures of $k$-monotone densities. Our general technique yields computationally efficient algorithms for all these problems, in many cases with provably optimal sample complexities (up to logarithmic factors) in all parameters.