On Efficient Variants of Segment Anything Model: A Survey

The Segment Anything Model (SAM) is a foundational model for image segmentation tasks, known for its strong generalization across diverse applications. However, its impressive performance comes with significant computational and resource demands, making it challenging to deploy in resource-limited environments such as mobile devices. To address this, a variety of SAM variants have been proposed to enhance efficiency without sacrificing accuracy. This survey provides the first comprehensive review of these efficient SAM variants. We begin by exploring the motivations driving this research. We then present core techniques used in SAM and model acceleration. This is followed by an in-depth analysis of various acceleration strategies, categorized by approach. Finally, we offer a unified and extensive evaluation of these methods, assessing their efficiency and accuracy on representative benchmarks, and providing a clear comparison of their overall performance.

Linear regression without correspondence

This article considers algorithmic and statistical aspects of linear regression when the correspondence between the covariates and the responses is unknown. First, a fully polynomial-time approximation scheme is given for the natural least squares optimization problem in any constant dimension. Next, in an average-case and noise-free setting where the responses exactly correspond to a linear function of i.i.d. draws from a standard multivariate normal distribution, an efficient algorithm based on lattice basis reduction is shown to exactly recover the unknown linear function in arbitrary dimension. Finally, lower bounds on the signal-to-noise ratio are established for approximate recovery of the unknown linear function by any estimator.

Near-Optimal Density Estimation in Near-Linear Time Using Variable-Width Histograms

Let $p$ be an unknown and arbitrary probability distribution over $[0,1)$. We consider the problem of {\em density estimation}, in which a learning algorithm is given i.i.d. draws from $p$ and must (with high probability) output a hypothesis distribution that is close to $p$. The main contribution of this paper is a highly efficient density estimation algorithm for learning using a variable-width histogram, i.e., a hypothesis distribution with a piecewise constant probability density function. In more detail, for any $k$ and $\epsilon$, we give an algorithm that makes $\tilde{O}(k/\epsilon^2)$ draws from $p$, runs in $\tilde{O}(k/\epsilon^2)$ time, and outputs a hypothesis distribution $h$ that is piecewise constant with $O(k \log^2(1/\epsilon))$ pieces. With high probability the hypothesis $h$ satisfies $d_{\mathrm{TV}}(p,h) \leq C \cdot \mathrm{opt}_k(p) + \epsilon$, where $d_{\mathrm{TV}}$ denotes the total variation distance (statistical distance), $C$ is a universal constant, and $\mathrm{opt}_k(p)$ is the smallest total variation distance between $p$ and any $k$-piecewise constant distribution. The sample size and running time of our algorithm are optimal up to logarithmic factors. The "approximation factor" $C$ in our result is inherent in the problem, as we prove that no algorithm with sample size bounded in terms of $k$ and $\epsilon$ can achieve $C<2$ regardless of what kind of hypothesis distribution it uses.

Efficient Density Estimation via Piecewise Polynomial Approximation

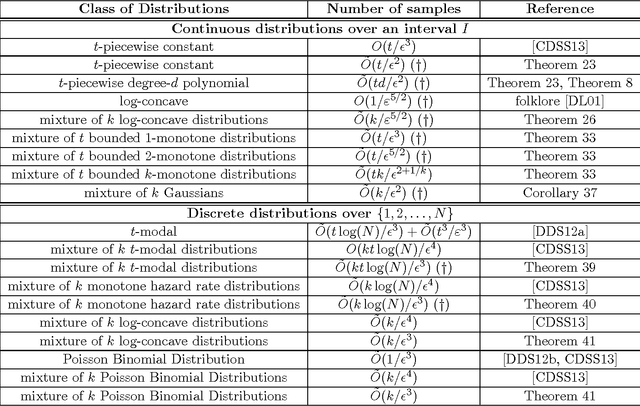
We give a highly efficient "semi-agnostic" algorithm for learning univariate probability distributions that are well approximated by piecewise polynomial density functions. Let $p$ be an arbitrary distribution over an interval $I$ which is $\tau$-close (in total variation distance) to an unknown probability distribution $q$ that is defined by an unknown partition of $I$ into $t$ intervals and $t$ unknown degree-$d$ polynomials specifying $q$ over each of the intervals. We give an algorithm that draws $\tilde{O}(t\new{(d+1)}/\eps^2)$ samples from $p$, runs in time $\poly(t,d,1/\eps)$, and with high probability outputs a piecewise polynomial hypothesis distribution $h$ that is $(O(\tau)+\eps)$-close (in total variation distance) to $p$. This sample complexity is essentially optimal; we show that even for $\tau=0$, any algorithm that learns an unknown $t$-piecewise degree-$d$ probability distribution over $I$ to accuracy $\eps$ must use $\Omega({\frac {t(d+1)} {\poly(1 + \log(d+1))}} \cdot {\frac 1 {\eps^2}})$ samples from the distribution, regardless of its running time. Our algorithm combines tools from approximation theory, uniform convergence, linear programming, and dynamic programming. We apply this general algorithm to obtain a wide range of results for many natural problems in density estimation over both continuous and discrete domains. These include state-of-the-art results for learning mixtures of log-concave distributions; mixtures of $t$-modal distributions; mixtures of Monotone Hazard Rate distributions; mixtures of Poisson Binomial Distributions; mixtures of Gaussians; and mixtures of $k$-monotone densities. Our general technique yields computationally efficient algorithms for all these problems, in many cases with provably optimal sample complexities (up to logarithmic factors) in all parameters.

Learning mixtures of structured distributions over discrete domains

Let $\mathfrak{C}$ be a class of probability distributions over the discrete domain $[n] = \{1,...,n\}.$ We show that if $\mathfrak{C}$ satisfies a rather general condition -- essentially, that each distribution in $\mathfrak{C}$ can be well-approximated by a variable-width histogram with few bins -- then there is a highly efficient (both in terms of running time and sample complexity) algorithm that can learn any mixture of $k$ unknown distributions from $\mathfrak{C}.$ We analyze several natural types of distributions over $[n]$, including log-concave, monotone hazard rate and unimodal distributions, and show that they have the required structural property of being well-approximated by a histogram with few bins. Applying our general algorithm, we obtain near-optimally efficient algorithms for all these mixture learning problems.