Implicit regularization for deep neural networks driven by an Ornstein-Uhlenbeck like process

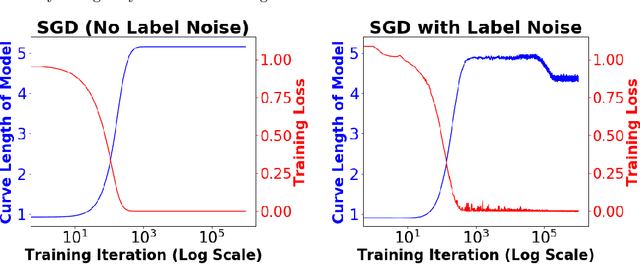
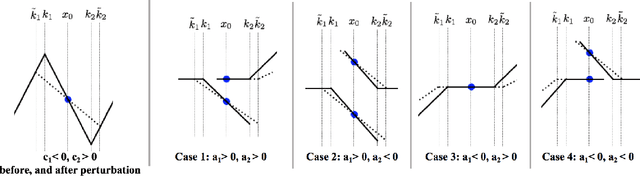
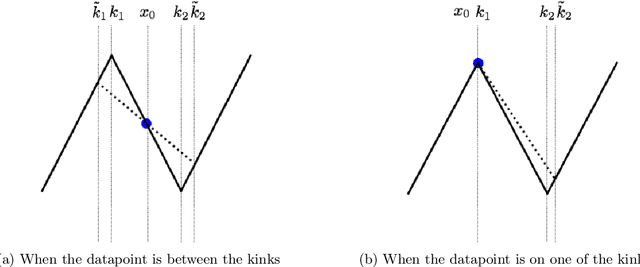
We consider deep networks, trained via stochastic gradient descent to minimize L2 loss, with the training labels perturbed by independent noise at each iteration. We characterize the behavior of the training dynamics near any parameter vector that achieves zero training error, in terms of an implicit regularization term corresponding to the sum over the data points, of the squared L2 norm of the gradient of the model with respect to the parameter vector, evaluated at each data point. We then leverage this general characterization, which holds for networks of any connectivity, width, depth, and choice of activation function, to show that for 2-layer ReLU networks of arbitrary width and L2 loss, when trained on one-dimensional labeled data $(x_1,y_1),\ldots,(x_n,y_n),$ the only stable solutions with zero training error correspond to functions that: 1) are linear over any set of three or more co-linear training points (i.e. the function has no extra "kinks"); and 2) change convexity the minimum number of times that is necessary to fit the training data. Additionally, for 2-layer networks of arbitrary width, with tanh or logistic activations, we show that when trained on a single $d$-dimensional point $(x,y)$ the only stable solutions correspond to networks where the activations of all hidden units at the datapoint, and all weights from the hidden units to the output, take at most two distinct values, or are zero. In this sense, we show that when trained on "simple" data, models corresponding to stable parameters are also "simple"; in short, despite fitting in an over-parameterized regime where the vast majority of expressible functions are complicated and badly behaved, stable parameters reached by training with noise express nearly the "simplest possible" hypothesis consistent with the data. These results shed light on the mystery of why deep networks generalize so well in practice.