Approximate resilience, monotonicity, and the complexity of agnostic learning
Paper and Code
Jul 09, 2014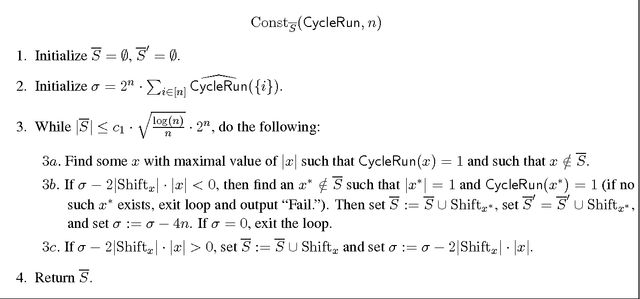
A function $f$ is $d$-resilient if all its Fourier coefficients of degree at most $d$ are zero, i.e., $f$ is uncorrelated with all low-degree parities. We study the notion of $\mathit{approximate}$ $\mathit{resilience}$ of Boolean functions, where we say that $f$ is $\alpha$-approximately $d$-resilient if $f$ is $\alpha$-close to a $[-1,1]$-valued $d$-resilient function in $\ell_1$ distance. We show that approximate resilience essentially characterizes the complexity of agnostic learning of a concept class $C$ over the uniform distribution. Roughly speaking, if all functions in a class $C$ are far from being $d$-resilient then $C$ can be learned agnostically in time $n^{O(d)}$ and conversely, if $C$ contains a function close to being $d$-resilient then agnostic learning of $C$ in the statistical query (SQ) framework of Kearns has complexity of at least $n^{\Omega(d)}$. This characterization is based on the duality between $\ell_1$ approximation by degree-$d$ polynomials and approximate $d$-resilience that we establish. In particular, it implies that $\ell_1$ approximation by low-degree polynomials, known to be sufficient for agnostic learning over product distributions, is in fact necessary. Focusing on monotone Boolean functions, we exhibit the existence of near-optimal $\alpha$-approximately $\widetilde{\Omega}(\alpha\sqrt{n})$-resilient monotone functions for all $\alpha>0$. Prior to our work, it was conceivable even that every monotone function is $\Omega(1)$-far from any $1$-resilient function. Furthermore, we construct simple, explicit monotone functions based on ${\sf Tribes}$ and ${\sf CycleRun}$ that are close to highly resilient functions. Our constructions are based on a fairly general resilience analysis and amplification. These structural results, together with the characterization, imply nearly optimal lower bounds for agnostic learning of monotone juntas.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge