Direction-adaptive Mamba: Spatial-Frequency Dual-Domain Collaborative Learning for PolSAR Image Classification

Deep learning dominates polarimetric synthetic aperture radar (PolSAR) image classification, with Mamba architectures serving as favorable backbones due to linear complexity and strong global modeling capacity. However, existing PolSAR Mamba methods have two critical flaws: pure spatial processing discards fine-grained edges and textures, and fixed scanning patterns fail to model direction-variant anisotropic scattering and weak boundaries essential for PolSAR physical analysis. This work proposes DA-Mamba, a direction-adaptive Mamba framework with dual-domain collaborative learning for PolSAR classification. Equipped with an edge-aligned direction-adaptive scanning scheme, DA-Mamba captures long-range spatial dependencies and accurate boundary details. It adopts the Non-Subsampled Contourlet Transform (NSCT) to separate PolSAR data into low-frequency global components and multi-directional high-frequency subbands, extracting anisotropic structural features from high-frequency information while preserving global context via low-frequency branches. A dual-domain collaborative learning module further integrates spatial scattering and frequency-domain representations to strengthen feature discriminability. Evaluated on three real-world PolSAR datasets, DA-Mamba surpasses state-of-the-art methods, verifying the efficacy of the proposed adaptive scanning and dual-domain fusion designs. Code will be publicly available.

WGDnet: Wishart-guided Geometric-aware Deep Network for PolSAR Image Classification

Polarimetric Synthetic Aperture Radar (PolSAR) classification underpins all-weather Earth observation. Conventional Wishart methods depend on rigid handcrafted operators with limited adaptability, while mainstream deep networks ignore PolSAR native Wishart scattering statistics. Additionally, fixed convolution windows fail to capture multi-scale, multi-directional terrain patterns, harming boundary detection and small-object characterization. To mitigate these drawbacks, we propose WGDNet, a Wishart-guided geometric-aware deep network. It integrates three core designs: (1) learnable Wishart convolutions with directional kernels for multi-scale statistical edge feature extraction; (2) an orientation-prior aggregation module that estimates dominant local directions and confidences to refine directional Wishart outputs adaptively; (3) GAnet, a scale-direction adaptive geometric-aware convolution that dynamically reshapes sampling grids to model anisotropic terrain and retain fine details. Our contributions lie in learnable Wishart statistical modeling, orientation-prior feature aggregation, and geometry-adaptive convolution. Evaluations across four real PolSAR datasets verify WGDNet surpasses existing state-of-the-art approaches in classification accuracy and boundary fidelity.

A Novel Riemannian Sparse Representation Learning Network for Polarimetric SAR Image Classification

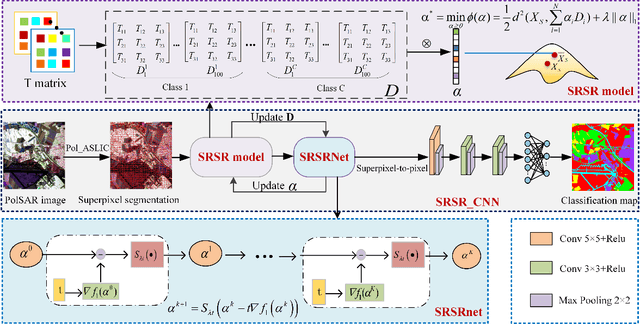
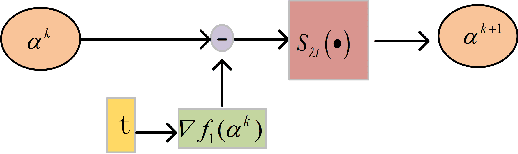
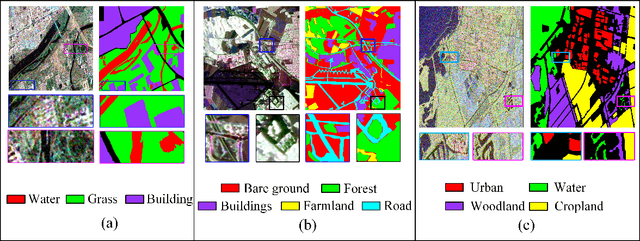
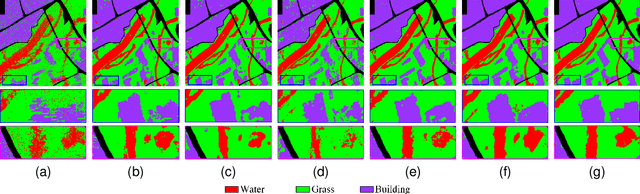
Deep learning is an effective end-to-end method for Polarimetric Synthetic Aperture Radar(PolSAR) image classification, but it lacks the guidance of related mathematical principle and is essentially a black-box model. In addition, existing deep models learn features in Euclidean space, where PolSAR complex matrix is commonly converted into a complex-valued vector as the network input, distorting matrix structure and channel relationship. However, the complex covariance matrix is Hermitian positive definite (HPD), and resides on a Riemannian manifold instead of a Euclidean one. Existing methods cannot measure the geometric distance of HPD matrices and easily cause some misclassifications due to inappropriate Euclidean measures. To address these issues, we propose a novel Riemannian Sparse Representation Learning Network (SRSR CNN) for PolSAR images. Firstly, a superpixel-based Riemannian Sparse Representation (SRSR) model is designed to learn the sparse features with Riemannian metric. Then, the optimization procedure of the SRSR model is inferred and further unfolded into an SRSRnet, which can automatically learn the sparse coefficients and dictionary atoms. Furthermore, to learn contextual high-level features, a CNN-enhanced module is added to improve classification performance. The proposed network is a Sparse Representation (SR) guided deep learning model, which can directly utilize the covariance matrix as the network input, and utilize Riemannian metric to learn geometric structure and sparse features of complex matrices in Riemannian space. Experiments on three real PolSAR datasets demonstrate that the proposed method surpasses state-of-the-art techniques in ensuring accurate edge details and correct region homogeneity for classification.

Riemannian Complex Hermit Positive Definite Convolution Network for Polarimetric SAR Image Classification

Deep learning can learn high-level semantic features in Euclidean space effectively for PolSAR images, while they need to covert the complex covariance matrix into a feature vector or complex-valued vector as the network input. However, the complex covariance matrices are essentially a complex Hermit positive definite (HPD) matrix endowed in Riemannian manifold rather than Euclidean space. The matrix's real and imagery parts are with the same significance, as the imagery part represents the phase information. The matrix vectorization will destroy the geometric structure and manifold characteristics of complex covariance matrices. To learn complex HPD matrices directly, we propose a Riemannian complex HPD convolution network(HPD\_CNN) for PolSAR images. This method consists of a complex HPD unfolding network(HPDnet) and a CV-3DCNN enhanced network. The proposed complex HPDnet defines the HPD mapping, rectifying and the logEig layers to learn geometric features of complex matrices. In addition, a fast eigenvalue decomposition method is designed to reduce computation burden. Finally, a Riemannian-to-Euclidean enhanced network is defined to enhance contextual information for classification. Experimental results on two real PolSSAR datasets demonstrate the proposed method can achieve superior performance than the state-of-the-art methods especially in heterogeneous regions.

Riemannian Complex Matrix Convolution Network for PolSAR Image Classification

Recently, deep learning methods have achieved superior performance for Polarimetric Synthetic Aperture Radar(PolSAR) image classification. Existing deep learning methods learn PolSAR data by converting the covariance matrix into a feature vector or complex-valued vector as the input. However, all these methods cannot learn the structure of complex matrix directly and destroy the channel correlation. To learn geometric structure of complex matrix, we propose a Riemannian complex matrix convolution network for PolSAR image classification in Riemannian space for the first time, which directly utilizes the complex matrix as the network input and defines the Riemannian operations to learn complex matrix's features. The proposed Riemannian complex matrix convolution network considers PolSAR complex matrix endowed in Riemannian manifold, and defines a series of new Riemannian convolution, ReLu and LogEig operations in Riemannian space, which breaks through the Euclidean constraint of conventional networks. Then, a CNN module is appended to enhance contextual Riemannian features. Besides, a fast kernel learning method is developed for the proposed method to learn class-specific features and reduce the computation time effectively. Experiments are conducted on three sets of real PolSAR data with different bands and sensors. Experiments results demonstrates the proposed method can obtain superior performance than the state-of-the-art methods.

Riemannian Nearest-Regularized Subspace Classification for Polarimetric SAR images

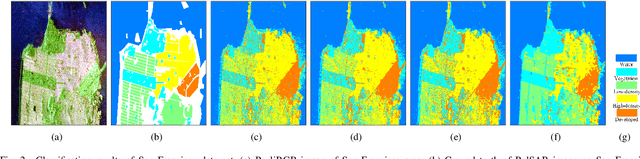
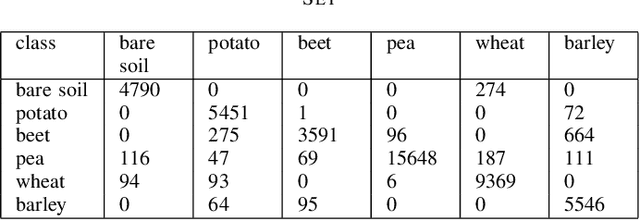
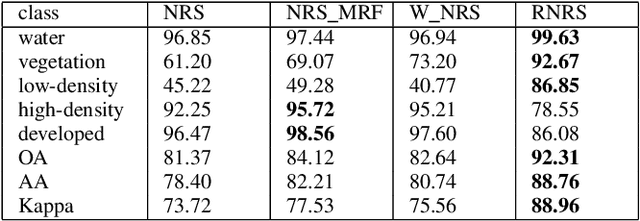
As a representation learning method, nearest regularized subspace(NRS) algorithm is an effective tool to obtain both accuracy and speed for PolSAR image classification. However, existing NRS methods use the polarimetric feature vector but the PolSAR original covariance matrix(known as Hermitian positive definite(HPD)matrix) as the input. Without considering the matrix structure, existing NRS-based methods cannot learn correlation among channels. How to utilize the original covariance matrix to NRS method is a key problem. To address this limit, a Riemannian NRS method is proposed, which consider the HPD matrices endow in the Riemannian space. Firstly, to utilize the PolSAR original data, a Riemannian NRS method(RNRS) is proposed by constructing HPD dictionary and HPD distance metric. Secondly, a new Tikhonov regularization term is designed to reduce the differences within the same class. Finally, the optimal method is developed and the first-order derivation is inferred. During the experimental test, only T matrix is used in the proposed method, while multiple of features are utilized for compared methods. Experimental results demonstrate the proposed method can outperform the state-of-art algorithms even using less features.

Polarimetric Hierarchical Semantic Model and Scattering Mechanism Based PolSAR Image Classification

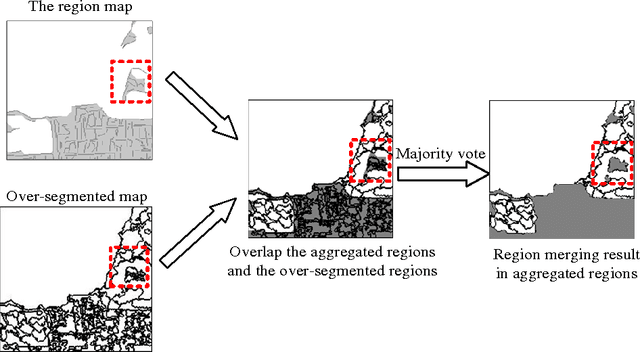
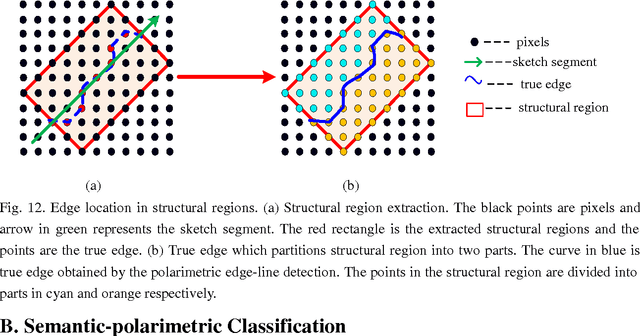
For polarimetric SAR (PolSAR) image classification, it is a challenge to classify the aggregated terrain types, such as the urban area, into semantic homogenous regions due to sharp bright-dark variations in intensity. The aggregated terrain type is formulated by the similar ground objects aggregated together. In this paper, a polarimetric hierarchical semantic model (PHSM) is firstly proposed to overcome this disadvantage based on the constructions of a primal-level and a middle-level semantic. The primal-level semantic is a polarimetric sketch map which consists of sketch segments as the sparse representation of a PolSAR image. The middle-level semantic is a region map which can extract semantic homogenous regions from the sketch map by exploiting the topological structure of sketch segments. Mapping the region map to the PolSAR image, a complex PolSAR scene is partitioned into aggregated, structural and homogenous pixel-level subspaces with the characteristics of relatively coherent terrain types in each subspace. Then, according to the characteristics of three subspaces above, three specific methods are adopted, and furthermore polarimetric information is exploited to improve the segmentation result. Experimental results on PolSAR data sets with different bands and sensors demonstrate that the proposed method is superior to the state-of-the-art methods in region homogeneity and edge preservation for terrain classification.