Haiyan Jin
A Novel Riemannian Sparse Representation Learning Network for Polarimetric SAR Image Classification
Feb 21, 2025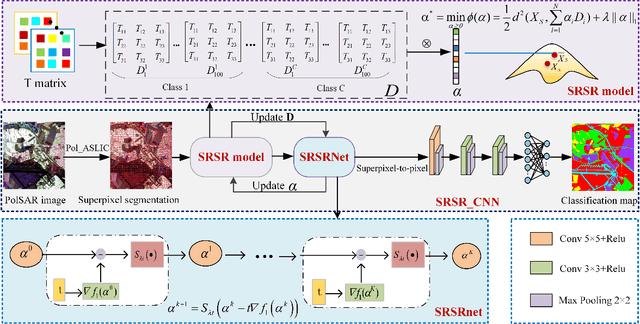
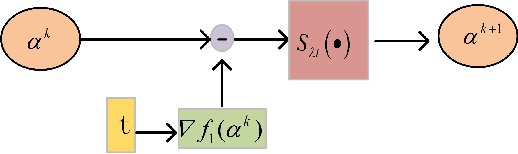
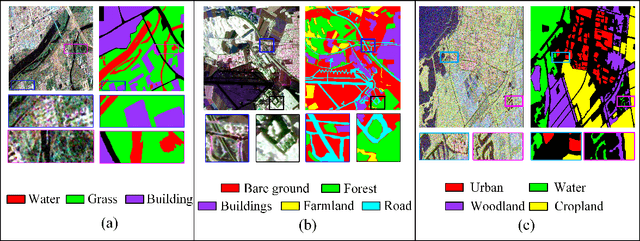
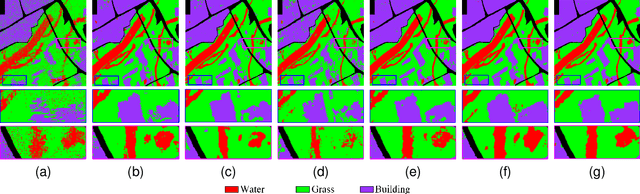
Abstract:Deep learning is an effective end-to-end method for Polarimetric Synthetic Aperture Radar(PolSAR) image classification, but it lacks the guidance of related mathematical principle and is essentially a black-box model. In addition, existing deep models learn features in Euclidean space, where PolSAR complex matrix is commonly converted into a complex-valued vector as the network input, distorting matrix structure and channel relationship. However, the complex covariance matrix is Hermitian positive definite (HPD), and resides on a Riemannian manifold instead of a Euclidean one. Existing methods cannot measure the geometric distance of HPD matrices and easily cause some misclassifications due to inappropriate Euclidean measures. To address these issues, we propose a novel Riemannian Sparse Representation Learning Network (SRSR CNN) for PolSAR images. Firstly, a superpixel-based Riemannian Sparse Representation (SRSR) model is designed to learn the sparse features with Riemannian metric. Then, the optimization procedure of the SRSR model is inferred and further unfolded into an SRSRnet, which can automatically learn the sparse coefficients and dictionary atoms. Furthermore, to learn contextual high-level features, a CNN-enhanced module is added to improve classification performance. The proposed network is a Sparse Representation (SR) guided deep learning model, which can directly utilize the covariance matrix as the network input, and utilize Riemannian metric to learn geometric structure and sparse features of complex matrices in Riemannian space. Experiments on three real PolSAR datasets demonstrate that the proposed method surpasses state-of-the-art techniques in ensuring accurate edge details and correct region homogeneity for classification.
Riemannian Complex Hermit Positive Definite Convolution Network for Polarimetric SAR Image Classification
Feb 12, 2025Abstract:Deep learning can learn high-level semantic features in Euclidean space effectively for PolSAR images, while they need to covert the complex covariance matrix into a feature vector or complex-valued vector as the network input. However, the complex covariance matrices are essentially a complex Hermit positive definite (HPD) matrix endowed in Riemannian manifold rather than Euclidean space. The matrix's real and imagery parts are with the same significance, as the imagery part represents the phase information. The matrix vectorization will destroy the geometric structure and manifold characteristics of complex covariance matrices. To learn complex HPD matrices directly, we propose a Riemannian complex HPD convolution network(HPD\_CNN) for PolSAR images. This method consists of a complex HPD unfolding network(HPDnet) and a CV-3DCNN enhanced network. The proposed complex HPDnet defines the HPD mapping, rectifying and the logEig layers to learn geometric features of complex matrices. In addition, a fast eigenvalue decomposition method is designed to reduce computation burden. Finally, a Riemannian-to-Euclidean enhanced network is defined to enhance contextual information for classification. Experimental results on two real PolSSAR datasets demonstrate the proposed method can achieve superior performance than the state-of-the-art methods especially in heterogeneous regions.
Riemannian Complex Matrix Convolution Network for PolSAR Image Classification
Dec 06, 2023Abstract:Recently, deep learning methods have achieved superior performance for Polarimetric Synthetic Aperture Radar(PolSAR) image classification. Existing deep learning methods learn PolSAR data by converting the covariance matrix into a feature vector or complex-valued vector as the input. However, all these methods cannot learn the structure of complex matrix directly and destroy the channel correlation. To learn geometric structure of complex matrix, we propose a Riemannian complex matrix convolution network for PolSAR image classification in Riemannian space for the first time, which directly utilizes the complex matrix as the network input and defines the Riemannian operations to learn complex matrix's features. The proposed Riemannian complex matrix convolution network considers PolSAR complex matrix endowed in Riemannian manifold, and defines a series of new Riemannian convolution, ReLu and LogEig operations in Riemannian space, which breaks through the Euclidean constraint of conventional networks. Then, a CNN module is appended to enhance contextual Riemannian features. Besides, a fast kernel learning method is developed for the proposed method to learn class-specific features and reduce the computation time effectively. Experiments are conducted on three sets of real PolSAR data with different bands and sensors. Experiments results demonstrates the proposed method can obtain superior performance than the state-of-the-art methods.
Riemannian Nearest-Regularized Subspace Classification for Polarimetric SAR images
Jan 02, 2022
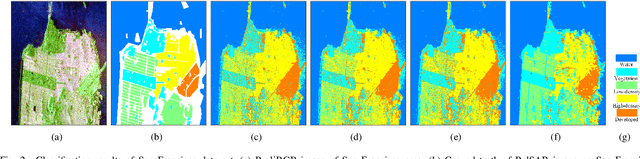
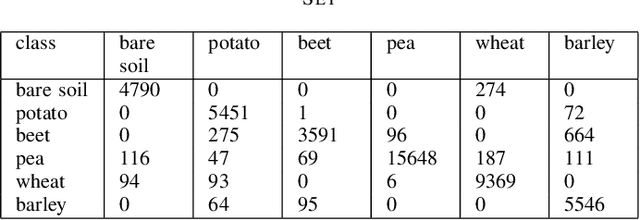
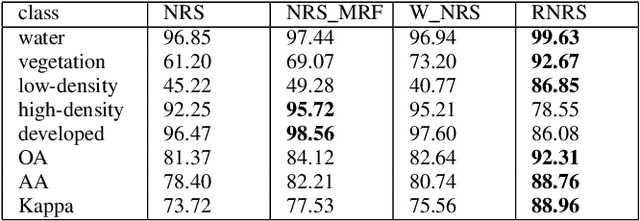
Abstract:As a representation learning method, nearest regularized subspace(NRS) algorithm is an effective tool to obtain both accuracy and speed for PolSAR image classification. However, existing NRS methods use the polarimetric feature vector but the PolSAR original covariance matrix(known as Hermitian positive definite(HPD)matrix) as the input. Without considering the matrix structure, existing NRS-based methods cannot learn correlation among channels. How to utilize the original covariance matrix to NRS method is a key problem. To address this limit, a Riemannian NRS method is proposed, which consider the HPD matrices endow in the Riemannian space. Firstly, to utilize the PolSAR original data, a Riemannian NRS method(RNRS) is proposed by constructing HPD dictionary and HPD distance metric. Secondly, a new Tikhonov regularization term is designed to reduce the differences within the same class. Finally, the optimal method is developed and the first-order derivation is inferred. During the experimental test, only T matrix is used in the proposed method, while multiple of features are utilized for compared methods. Experimental results demonstrate the proposed method can outperform the state-of-art algorithms even using less features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge