Latent Complete Row Space Recovery for Multi-view Subspace Clustering

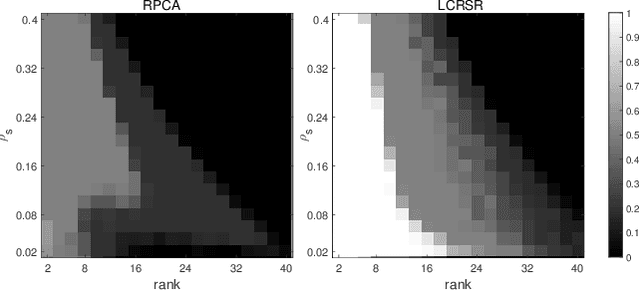
Multi-view subspace clustering has been applied to applications such as image processing and video surveillance, and has attracted increasing attention. Most existing methods learn view-specific self-representation matrices, and construct a combined affinity matrix from multiple views. The affinity construction process is time-consuming, and the combined affinity matrix is not guaranteed to reflect the whole true subspace structure. To overcome these issues, the Latent Complete Row Space Recovery (LCRSR) method is proposed. Concretely, LCRSR is based on the assumption that the multi-view observations are generated from an underlying latent representation, which is further assumed to collect the authentic samples drawn exactly from multiple subspaces. LCRSR is able to recover the row space of the latent representation, which not only carries complete information from multiple views but also determines the subspace membership under certain conditions. LCRSR does not involve the graph construction procedure and is solved with an efficient and convergent algorithm, thereby being more scalable to large-scale datasets. The effectiveness and efficiency of LCRSR are validated by clustering various kinds of multi-view data and illustrated in the background subtraction task.

Dictionary Learning with BLOTLESS Update

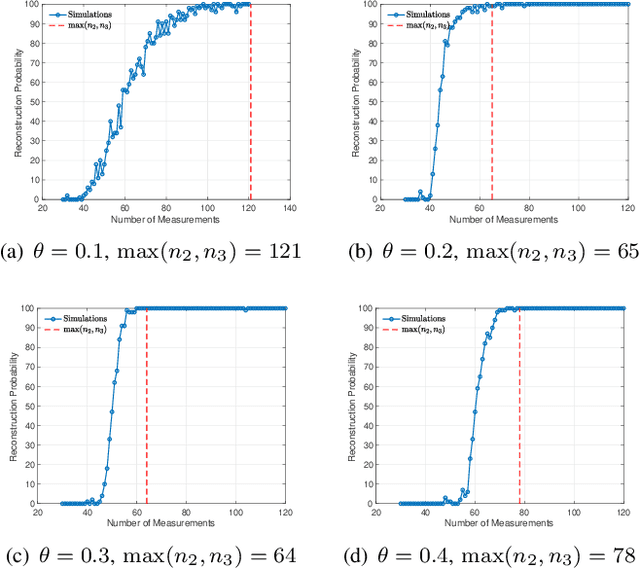
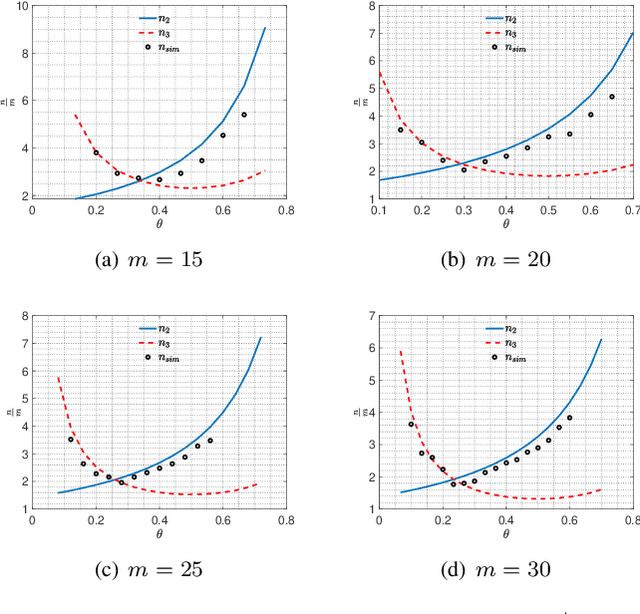
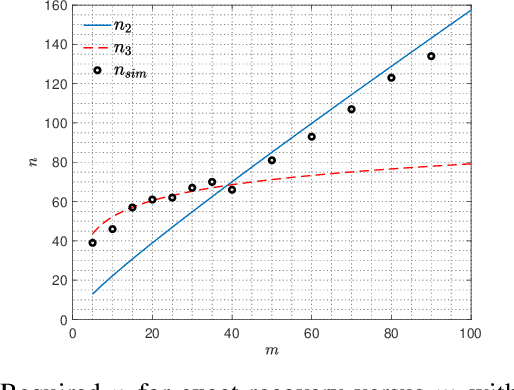
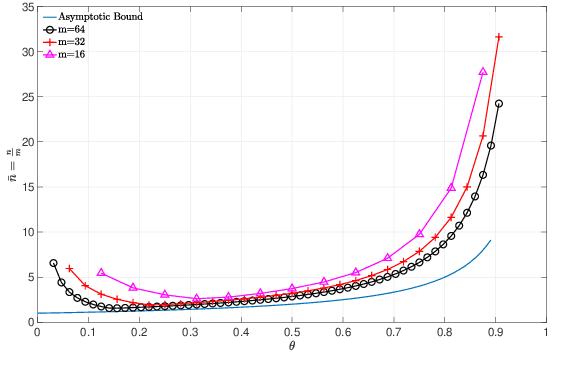
Algorithms for learning a dictionary under which a data in a given set have sparse expansions typically alternate between sparse coding and dictionary update stages. Methods for dictionary update aim to minimise expansion error by updating dictionary vectors and expansion coefficients given patterns of non-zero coefficients obtained in the sparse coding stage. We propose a block total least squares (BLOTLESS) algorithm for dictionary update. BLOTLESS updates a block of dictionary elements and the corresponding sparse coefficients simultaneously. In the error free case, three necessary conditions for exact recovery are identified. Lower bounds on the number of training data are established so that the necessary conditions hold with high probability. Numerical simulations show that the bounds well approximate the number of training data needed for exact dictionary recovery. Numerical experiments further demonstrate several benefits of dictionary learning with BLOTLESS update compared with state-of-the-art algorithms especially when the amount of training data is small.

Joint Embedding Learning and Low-Rank Approximation: A Framework for Incomplete Multi-view Learning

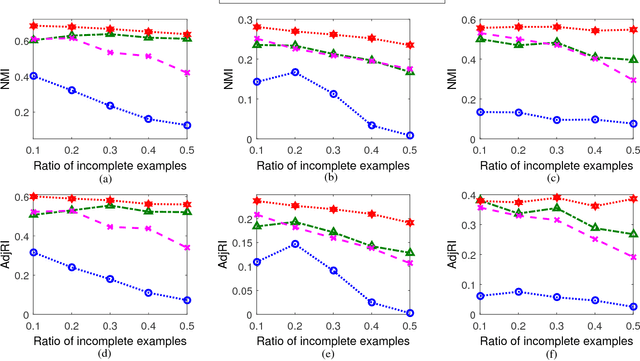
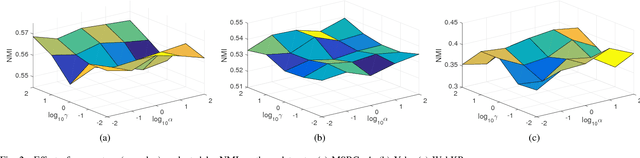
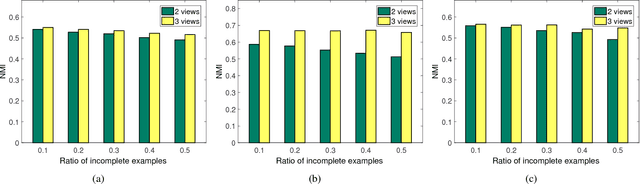
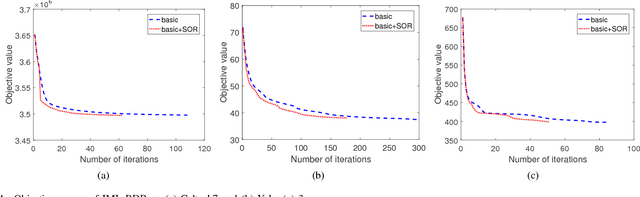
In real-world applications, not all instances in multi-view data are fully represented. To deal with incomplete multi-view data, traditional multi-view algorithms usually throw away the incomplete instances, resulting in loss of available information. To overcome this loss, Incomplete Multi-view Learning (IML) has become a hot research topic. In this paper, we propose a general IML framework for unifying existing IML methods and gaining insight into IML. The proposed framework jointly performs embedding learning and low-rank approximation. Concretely, it approximates the incomplete data by a set of low-rank matrices and learns a full and common embedding by linear transformation. Several existing IML methods can be unified as special cases of the framework. More interestingly, some linear transformation based full-view methods can be adapted to IML directly with the guidance of the framework. This bridges the gap between full multi-view learning and IML. Moreover, the framework can provide guidance for developing new algorithms. For illustration, within the framework, we propose a specific method, termed as Incomplete Multi-view Learning with Block Diagonal Representation (IML-BDR). Based on the assumption that the sampled examples have approximate linear subspace structure, IML-BDR uses the block diagonal structure prior to learn the full embedding, which would lead to more correct clustering. A convergent alternating iterative algorithm with the Successive Over-Relaxation (SOR) optimization technique is devised for optimization. Experimental results on various datasets demonstrate the effectiveness of IML-BDR.

Strongly Convex Programming for Exact Matrix Completion and Robust Principal Component Analysis

The common task in matrix completion (MC) and robust principle component analysis (RPCA) is to recover a low-rank matrix from a given data matrix. These problems gained great attention from various areas in applied sciences recently, especially after the publication of the pioneering works of Cand`es et al.. One fundamental result in MC and RPCA is that nuclear norm based convex optimizations lead to the exact low-rank matrix recovery under suitable conditions. In this paper, we extend this result by showing that strongly convex optimizations can guarantee the exact low-rank matrix recovery as well. The result in this paper not only provides sufficient conditions under which the strongly convex models lead to the exact low-rank matrix recovery, but also guides us on how to choose suitable parameters in practical algorithms.