Latent Complete Row Space Recovery for Multi-view Subspace Clustering

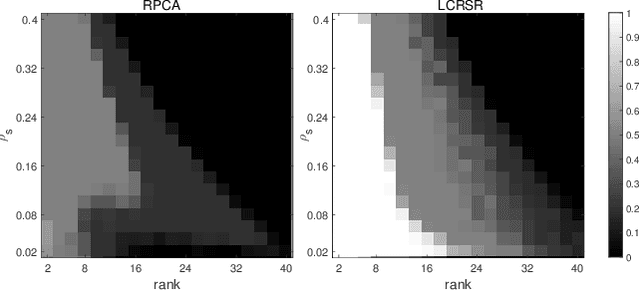
Multi-view subspace clustering has been applied to applications such as image processing and video surveillance, and has attracted increasing attention. Most existing methods learn view-specific self-representation matrices, and construct a combined affinity matrix from multiple views. The affinity construction process is time-consuming, and the combined affinity matrix is not guaranteed to reflect the whole true subspace structure. To overcome these issues, the Latent Complete Row Space Recovery (LCRSR) method is proposed. Concretely, LCRSR is based on the assumption that the multi-view observations are generated from an underlying latent representation, which is further assumed to collect the authentic samples drawn exactly from multiple subspaces. LCRSR is able to recover the row space of the latent representation, which not only carries complete information from multiple views but also determines the subspace membership under certain conditions. LCRSR does not involve the graph construction procedure and is solved with an efficient and convergent algorithm, thereby being more scalable to large-scale datasets. The effectiveness and efficiency of LCRSR are validated by clustering various kinds of multi-view data and illustrated in the background subtraction task.

Joint Embedding Learning and Low-Rank Approximation: A Framework for Incomplete Multi-view Learning

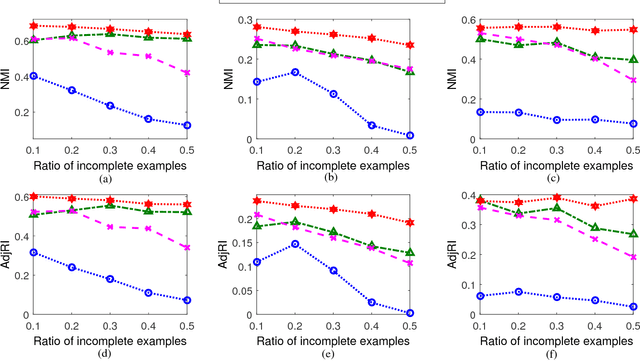
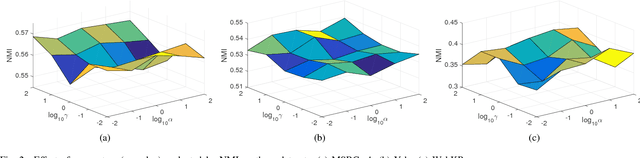
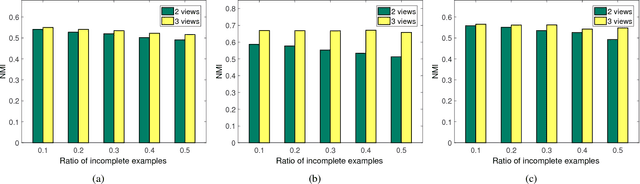
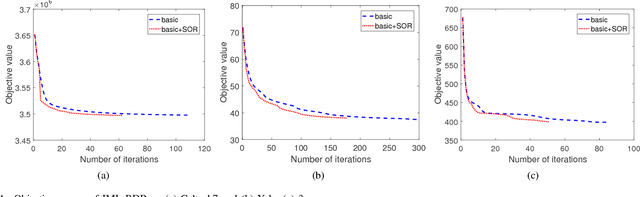
In real-world applications, not all instances in multi-view data are fully represented. To deal with incomplete multi-view data, traditional multi-view algorithms usually throw away the incomplete instances, resulting in loss of available information. To overcome this loss, Incomplete Multi-view Learning (IML) has become a hot research topic. In this paper, we propose a general IML framework for unifying existing IML methods and gaining insight into IML. The proposed framework jointly performs embedding learning and low-rank approximation. Concretely, it approximates the incomplete data by a set of low-rank matrices and learns a full and common embedding by linear transformation. Several existing IML methods can be unified as special cases of the framework. More interestingly, some linear transformation based full-view methods can be adapted to IML directly with the guidance of the framework. This bridges the gap between full multi-view learning and IML. Moreover, the framework can provide guidance for developing new algorithms. For illustration, within the framework, we propose a specific method, termed as Incomplete Multi-view Learning with Block Diagonal Representation (IML-BDR). Based on the assumption that the sampled examples have approximate linear subspace structure, IML-BDR uses the block diagonal structure prior to learn the full embedding, which would lead to more correct clustering. A convergent alternating iterative algorithm with the Successive Over-Relaxation (SOR) optimization technique is devised for optimization. Experimental results on various datasets demonstrate the effectiveness of IML-BDR.

Effective Discriminative Feature Selection with Non-trivial Solutions

Feature selection and feature transformation, the two main ways to reduce dimensionality, are often presented separately. In this paper, a feature selection method is proposed by combining the popular transformation based dimensionality reduction method Linear Discriminant Analysis (LDA) and sparsity regularization. We impose row sparsity on the transformation matrix of LDA through ${\ell}_{2,1}$-norm regularization to achieve feature selection, and the resultant formulation optimizes for selecting the most discriminative features and removing the redundant ones simultaneously. The formulation is extended to the ${\ell}_{2,p}$-norm regularized case: which is more likely to offer better sparsity when $0<p<1$. Thus the formulation is a better approximation to the feature selection problem. An efficient algorithm is developed to solve the ${\ell}_{2,p}$-norm based optimization problem and it is proved that the algorithm converges when $0<p\le 2$. Systematical experiments are conducted to understand the work of the proposed method. Promising experimental results on various types of real-world data sets demonstrate the effectiveness of our algorithm.