Agentic Reasoning and Tool Integration for LLMs via Reinforcement Learning

Large language models (LLMs) have achieved remarkable progress in complex reasoning tasks, yet they remain fundamentally limited by their reliance on static internal knowledge and text-only reasoning. Real-world problem solving often demands dynamic, multi-step reasoning, adaptive decision making, and the ability to interact with external tools and environments. In this work, we introduce ARTIST (Agentic Reasoning and Tool Integration in Self-improving Transformers), a unified framework that tightly couples agentic reasoning, reinforcement learning, and tool integration for LLMs. ARTIST enables models to autonomously decide when, how, and which tools to invoke within multi-turn reasoning chains, leveraging outcome-based RL to learn robust strategies for tool use and environment interaction without requiring step-level supervision. Extensive experiments on mathematical reasoning and multi-turn function calling benchmarks show that ARTIST consistently outperforms state-of-the-art baselines, with up to 22% absolute improvement over base models and strong gains on the most challenging tasks. Detailed studies and metric analyses reveal that agentic RL training leads to deeper reasoning, more effective tool use, and higher-quality solutions. Our results establish agentic RL with tool integration as a powerful new frontier for robust, interpretable, and generalizable problem-solving in LLMs.

Mechanistic Behavior Editing of Language Models

Large Language Models trained on web-scale text acquire language generation abilities that can solve a wide range of tasks, particularly when task knowledge is refined into the generative prior using in-context examples. However, spurious features learned from noisy data hinder their generalizability. Supervised finetuning can introduce task specificity, but introduce data inefficiency. Prior studies indicate that (i) noisy neural circuitries coexist with generalizable ones within LLMs, and (ii) finetuning typically enhances (or suppresses) existing abilities without introducing newer ones. Building upon these, we propose TaRot, a novel method for task adaptation. TaRot intervenes in the neural circuitries using learnable rotation matrices that are optimized using Bayesian Optimization, on labelled samples in the order of standard few-shot prompting examples. Experiments on multiple classification and generation tasks using LLMs of varying sizes reveal the efficacy of TaRot, improving upon both zero- as well as few-shot performance, with average improvements (across models and tasks) of 23.81% and 11.15%, respectively. The source code is available at https://github.com/joykirat18/TaRot

Exposing the Achilles' Heel: Evaluating LLMs Ability to Handle Mistakes in Mathematical Reasoning

Large Language Models (LLMs) have been applied to Math Word Problems (MWPs) with transformative impacts, revolutionizing how these complex problems are approached and solved in various domains including educational settings. However, the evaluation of these models often prioritizes final accuracy, overlooking the crucial aspect of reasoning capabilities. This work addresses this gap by focusing on the ability of LLMs to detect and correct reasoning mistakes. We introduce a novel dataset MWP-MISTAKE, incorporating MWPs with both correct and incorrect reasoning steps generated through rule-based methods and smaller language models. Our comprehensive benchmarking reveals significant insights into the strengths and weaknesses of state-of-the-art models, such as GPT-4o, GPT-4, GPT-3.5Turbo, and others. We highlight GPT-$o's superior performance in mistake detection and rectification and the persistent challenges faced by smaller models. Additionally, we identify issues related to data contamination and memorization, impacting the reliability of LLMs in real-world applications. Our findings emphasize the importance of rigorous evaluation of reasoning processes and propose future directions to enhance the generalization and robustness of LLMs in mathematical problem-solving.

EROS: Entity-Driven Controlled Policy Document Summarization

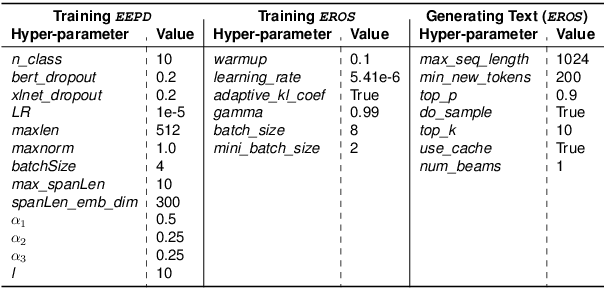
Privacy policy documents have a crucial role in educating individuals about the collection, usage, and protection of users' personal data by organizations. However, they are notorious for their lengthy, complex, and convoluted language especially involving privacy-related entities. Hence, they pose a significant challenge to users who attempt to comprehend organization's data usage policy. In this paper, we propose to enhance the interpretability and readability of policy documents by using controlled abstractive summarization -- we enforce the generated summaries to include critical privacy-related entities (e.g., data and medium) and organization's rationale (e.g.,target and reason) in collecting those entities. To achieve this, we develop PD-Sum, a policy-document summarization dataset with marked privacy-related entity labels. Our proposed model, EROS, identifies critical entities through a span-based entity extraction model and employs them to control the information content of the summaries using proximal policy optimization (PPO). Comparison shows encouraging improvement over various baselines. Furthermore, we furnish qualitative and human evaluations to establish the efficacy of EROS.

How to think step-by-step: A mechanistic understanding of chain-of-thought reasoning

Despite superior reasoning prowess demonstrated by Large Language Models (LLMs) with Chain-of-Thought (CoT) prompting, a lack of understanding prevails around the internal mechanisms of the models that facilitate CoT generation. This work investigates the neural sub-structures within LLMs that manifest CoT reasoning from a mechanistic point of view. From an analysis of LLaMA-2 7B applied to multistep reasoning over fictional ontologies, we demonstrate that LLMs deploy multiple parallel pathways of answer generation for step-by-step reasoning. These parallel pathways provide sequential answers from the input question context as well as the generated CoT. We observe a striking functional rift in the middle layers of the LLM. Token representations in the initial half remain strongly biased towards the pretraining prior, with the in-context taking over abruptly in the later half. This internal phase shift manifests in different functional components: attention heads that write the answer token predominantly appear in the later half, attention heads that move information along ontological relationships appear exclusively in the initial half, and so on. To the best of our knowledge, this is the first attempt towards mechanistic investigation of CoT reasoning in LLMs.

Frugal LMs Trained to Invoke Symbolic Solvers Achieve Parameter-Efficient Arithmetic Reasoning

Large Language Models (LLM) exhibit zero-shot mathematical reasoning capacity as a behavior emergent with scale, commonly manifesting as chain-of-thoughts (CoT) reasoning. However, multiple empirical findings suggest that this prowess is exclusive to LLMs with exorbitant sizes (beyond 50 billion parameters). Meanwhile, educational neuroscientists suggest that symbolic algebraic manipulation be introduced around the same time as arithmetic word problems to modularize language-to-formulation, symbolic manipulation of the formulation, and endgame arithmetic. In this paper, we start with the hypothesis that much smaller LMs, which are weak at multi-step reasoning, can achieve reasonable arithmetic reasoning if arithmetic word problems are posed as a formalize-then-solve task. In our architecture, which we call SYRELM, the LM serves the role of a translator to map natural language arithmetic questions into a formal language (FL) description. A symbolic solver then evaluates the FL expression to obtain the answer. A small frozen LM, equipped with an efficient low-rank adapter, is capable of generating FL expressions that incorporate natural language descriptions of the arithmetic problem (e.g., variable names and their purposes, formal expressions combining variables, etc.). We adopt policy-gradient reinforcement learning to train the adapted LM, informed by the non-differentiable symbolic solver. This marks a sharp departure from the recent development in tool-augmented LLMs, in which the external tools (e.g., calculator, Web search, etc.) are essentially detached from the learning phase of the LM. SYRELM shows massive improvements (e.g., +30.65 absolute point improvement in accuracy on the SVAMP dataset using GPT-J 6B model) over base LMs, while keeping our testbed easy to diagnose, interpret and within reach of most researchers.