Fourier-Net: Fast Image Registration with Band-limited Deformation

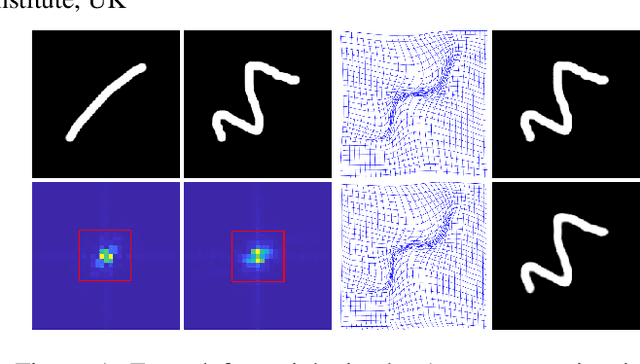
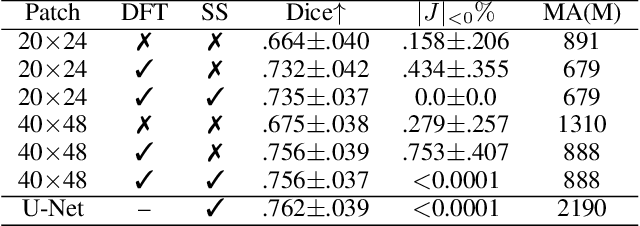
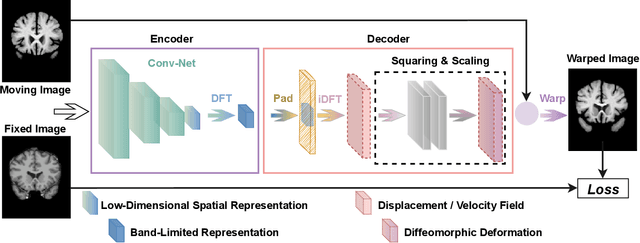
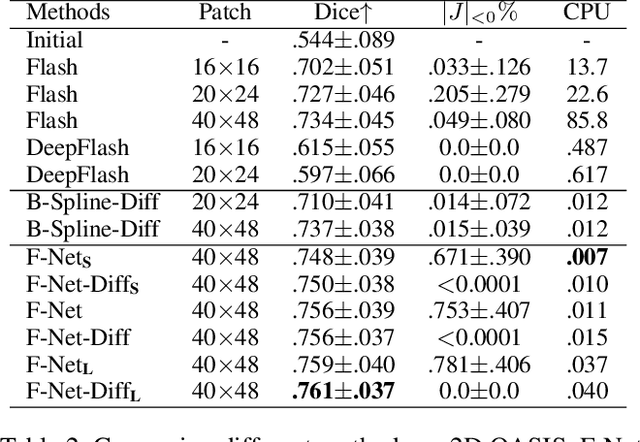
Unsupervised image registration commonly adopts U-Net style networks to predict dense displacement fields in the full-resolution spatial domain. For high-resolution volumetric image data, this process is however resource intensive and time-consuming. To tackle this problem, we propose the Fourier-Net, replacing the expansive path in a U-Net style network with a parameter-free model-driven decoder. Specifically, instead of our Fourier-Net learning to output a full-resolution displacement field in the spatial domain, we learn its low-dimensional representation in a band-limited Fourier domain. This representation is then decoded by our devised model-driven decoder (consisting of a zero padding layer and an inverse discrete Fourier transform layer) to the dense, full-resolution displacement field in the spatial domain. These changes allow our unsupervised Fourier-Net to contain fewer parameters and computational operations, resulting in faster inference speeds. Fourier-Net is then evaluated on two public 3D brain datasets against various state-of-the-art approaches. For example, when compared to a recent transformer-based method, i.e., TransMorph, our Fourier-Net, only using 0.22$\%$ of its parameters and 6.66$\%$ of the mult-adds, achieves a 0.6\% higher Dice score and an 11.48$\times$ faster inference speed. Code is available at \url{https://github.com/xi-jia/Fourier-Net}.

U-Net vs Transformer: Is U-Net Outdated in Medical Image Registration?

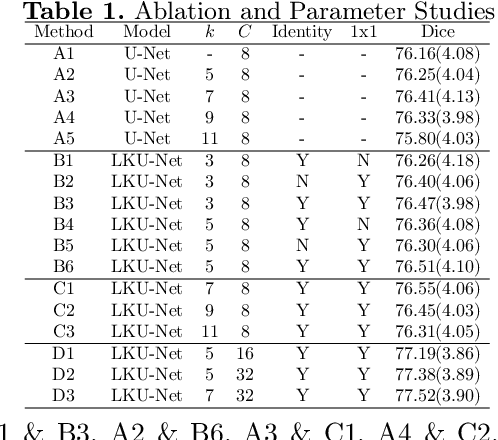
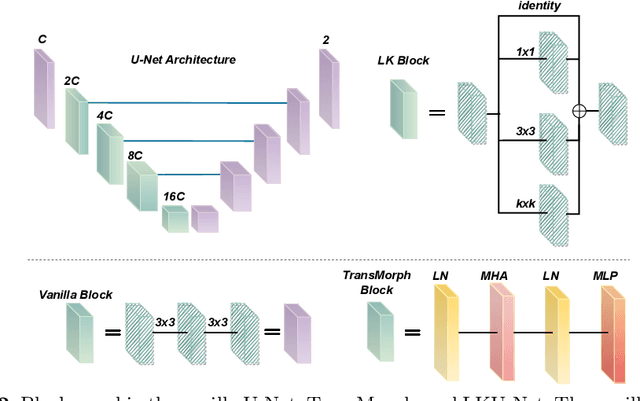
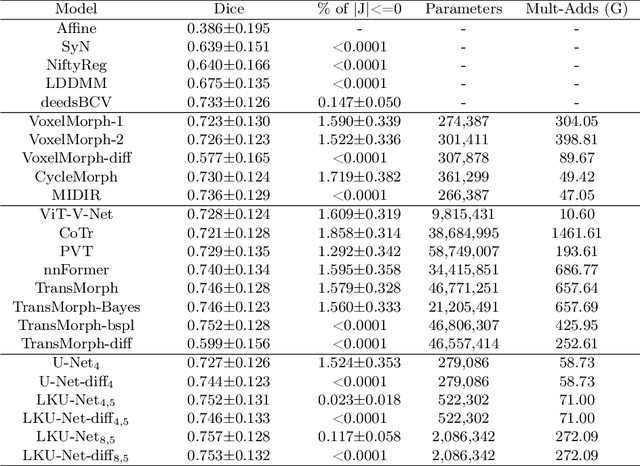
Due to their extreme long-range modeling capability, vision transformer-based networks have become increasingly popular in deformable image registration. We believe, however, that the receptive field of a 5-layer convolutional U-Net is sufficient to capture accurate deformations without needing long-range dependencies. The purpose of this study is therefore to investigate whether U-Net-based methods are outdated compared to modern transformer-based approaches when applied to medical image registration. For this, we propose a large kernel U-Net (LKU-Net) by embedding a parallel convolutional block to a vanilla U-Net in order to enhance the effective receptive field. On the public 3D IXI brain dataset for atlas-based registration, we show that the performance of the vanilla U-Net is already comparable with that of state-of-the-art transformer-based networks (such as TransMorph), and that the proposed LKU-Net outperforms TransMorph by using only 1.12% of its parameters and 10.8% of its mult-adds operations. We further evaluate LKU-Net on a MICCAI Learn2Reg 2021 challenge dataset for inter-subject registration, our LKU-Net also outperforms TransMorph on this dataset and ranks first on the public leaderboard as of the submission of this work. With only modest modifications to the vanilla U-Net, we show that U-Net can outperform transformer-based architectures on inter-subject and atlas-based 3D medical image registration. Code is available at https://github.com/xi-jia/LKU-Net.

Structure Unbiased Adversarial Model for Medical Image Segmentation

Generative models have been widely proposed in image recognition to generate more images where the distribution is similar to that of the real images. It often introduces a discriminator network to discriminate original real data and generated data. However, such discriminator often considers the distribution of the data and did not pay enough attention to the intrinsic gap due to structure. In this paper, we reformulate a new image to image translation problem to reduce structural gap, in addition to the typical intensity distribution gap. We further propose a simple yet important Structure Unbiased Adversarial Model for Medical Image Segmentation (SUAM) with learnable inverse structural deformation for medical image segmentation. It consists of a structure extractor, an attention diffeomorphic registration and a structure \& intensity distribution rendering module. The structure extractor aims to extract the dominant structure of the input image. The attention diffeomorphic registration is proposed to reduce the structure gap with an inverse deformation field to warp the prediction masks back to their original form. The structure rendering module is to render the deformed structure to an image with targeted intensity distribution. We apply the proposed SUAM on both optical coherence tomography (OCT), magnetic resonance imaging (MRI) and computerized tomography (CT) data. Experimental results show that the proposed method has the capability to transfer both intensity and structure distributions.

Accelerated First Order Methods for Variational Imaging

In this thesis, we offer a thorough investigation of different regularisation terms used in variational imaging problems, together with detailed optimisation processes of these problems. We begin by studying smooth problems and partially non-smooth problems in the form of Tikhonov denoising and Total Variation (TV) denoising, respectively. For Tikhonov denoising, we study an accelerated gradient method with adaptive restart, which shows a very rapid convergence rate. However, it is not straightforward to apply this fast algorithm to TV denoising, due to the non-smoothness of its built-in regularisation. To tackle this issue, we propose to utilise duality to convert such a non-smooth problem into a smooth one so that the accelerated gradient method with restart applies naturally. However, we notice that both Tikhonov and TV regularisations have drawbacks, in the form of blurred image edges and staircase artefacts, respectively. To overcome these drawbacks, we propose a novel adaption to Total Generalised Variation (TGV) regularisation called Total Smooth Variation (TSV), which retains edges and meanwhile does not produce results which contain staircase artefacts. To optimise TSV effectively, we then propose the Accelerated Proximal Gradient Algorithm (APGA) which also utilises adaptive restart techniques. Compared to existing state-of-the-art regularisations (e.g. TV), TSV is shown to obtain more effective results on denoising problems as well as advanced imaging applications such as magnetic resonance imaging (MRI) reconstruction and optical flow. TSV removes the staircase artefacts observed when using TV regularisation, but has the added advantage over TGV that it can be efficiently optimised using gradient based methods with Nesterov acceleration and adaptive restart. Code is available at https://github.com/Jbartlett6/Accelerated-First-Order-Method-for-Variational-Imaging.