A Comparison Between Lie Group- and Lie Algebra- Based Potential Functions for Geometric Impedance Control

In this paper, a comparison analysis between geometric impedance controls (GICs) derived from two different potential functions on SE(3) for robotic manipulators is presented. The first potential function is defined on the Lie group, utilizing the Frobenius norm of the configuration error matrix. The second potential function is defined utilizing the Lie algebra, i.e., log-map of the configuration error. Using a differential geometric approach, the detailed derivation of the distance metric and potential function on SE(3) is introduced. The GIC laws are respectively derived from the two potential functions, followed by extensive comparison analyses. In the qualitative analysis, the properties of the error function and control laws are analyzed, while the performances of the controllers are quantitatively compared using numerical simulation.

Clustering Techniques for Stable Linear Dynamical Systems with applications to Hard Disk Drives

In Robust Control and Data Driven Robust Control design methodologies, multiple plant transfer functions or a family of transfer functions are considered and a common controller is designed such that all the plants that fall into this family are stabilized. Though the plants are stabilized, the controller might be sub-optimal for each of the plants when the variations in the plants are large. This paper presents a way of clustering stable linear dynamical systems for the design of robust controllers within each of the clusters such that the controllers are optimal for each of the clusters. First a k-medoids algorithm for hard clustering will be presented for stable Linear Time Invariant (LTI) systems and then a Gaussian Mixture Models (GMM) clustering for a special class of LTI systems, common for Hard Disk Drive plants, will be presented.

Denoising Heat-inspired Diffusion with Insulators for Collision Free Motion Planning

Diffusion models have risen as a powerful tool in robotics due to their flexibility and multi-modality. While some of these methods effectively address complex problems, they often depend heavily on inference-time obstacle detection and require additional equipment. Addressing these challenges, we present a method that, during inference time, simultaneously generates only reachable goals and plans motions that avoid obstacles, all from a single visual input. Central to our approach is the novel use of a collision-avoiding diffusion kernel for training. Through evaluations against behavior-cloning and classical diffusion models, our framework has proven its robustness. It is particularly effective in multi-modal environments, navigating toward goals and avoiding unreachable ones blocked by obstacles, while ensuring collision avoidance.

Diffusion-EDFs: Bi-equivariant Denoising Generative Modeling on SE(3) for Visual Robotic Manipulation

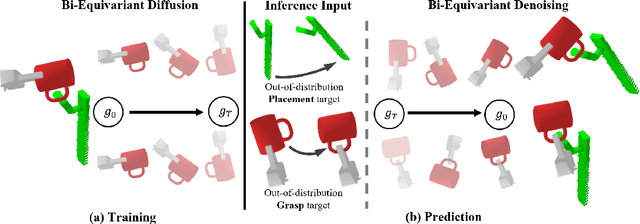
Recent studies have verified that equivariant methods can significantly improve the data efficiency, generalizability, and robustness in robot learning. Meanwhile, denoising diffusion-based generative modeling has recently gained significant attention as a promising approach for robotic manipulation learning from demonstrations with stochastic behaviors. In this paper, we present Diffusion-EDFs, a novel approach that incorporates spatial roto-translation equivariance, i.e., SE(3)-equivariance to diffusion generative modeling. By integrating SE(3)-equivariance into our model architectures, we demonstrate that our proposed method exhibits remarkable data efficiency, requiring only 5 to 10 task demonstrations for effective end-to-end training. Furthermore, our approach showcases superior generalizability compared to previous diffusion-based manipulation methods.

Robot Manipulation Task Learning by Leveraging SE(3) Group Invariance and Equivariance

This paper presents a differential geometric control approach that leverages SE(3) group invariance and equivariance to increase transferability in learning robot manipulation tasks that involve interaction with the environment. Specifically, we employ a control law and a learning representation framework that remain invariant under arbitrary SE(3) transformations of the manipulation task definition. Furthermore, the control law and learning representation framework are shown to be SE(3) equivariant when represented relative to the spatial frame. The proposed approach is based on utilizing a recently presented geometric impedance control (GIC) combined with a learning variable impedance control framework, where the gain scheduling policy is trained in a supervised learning fashion from expert demonstrations. A geometrically consistent error vector (GCEV) is fed to a neural network to achieve a gain scheduling policy that remains invariant to arbitrary translation and rotations. A comparison of our proposed control and learning framework with a well-known Cartesian space learning impedance control, equipped with a Cartesian error vector-based gain scheduling policy, confirms the significantly superior learning transferability of our proposed approach. A hardware implementation on a peg-in-hole task is conducted to validate the learning transferability and feasibility of the proposed approach.

Vision and Control for Grasping Clear Plastic Bags

We develop two novel vision methods for planning effective grasps for clear plastic bags, as well as a control method to enable a Sawyer arm with a parallel gripper to execute the grasps. The first vision method is based on classical image processing and heuristics (e.g., Canny edge detection) to select a grasp target and angle. The second uses a deep-learning model trained on a human-labeled data set to mimic human grasp decisions. A clustering algorithm is used to de-noise the outputs of each vision method. Subsequently, a workspace PD control method is used to execute each grasp. Of the two vision methods, we find the deep-learning based method to be more effective.

Geometric Impedance Control on SE for Robotic Manipulators

After its introduction, impedance control has been utilized as a primary control scheme for robotic manipulation tasks that involve interaction with unknown environments. While impedance control has been extensively studied, the geometric structure of SE(3) for the robotic manipulator itself and its use in formulating a robotic task has not been adequately addressed. In this paper, we propose a differential geometric approach to impedance control. Given a left-invariant error metric in SE(3), the corresponding error vectors in position and velocity are first derived. Using these geometrically consistent error vectors, we propose a novel impedance control scheme, which adequately accounts for the geometric structure of the manipulator in SE(3). The closed-loop stability for the proposed control schemes is verified using a Lyapunov function-based analysis. The proposed control design clearly outperformed a conventional impedance control approach when tracking challenging trajectory profiles.