A Comparison Between Lie Group- and Lie Algebra- Based Potential Functions for Geometric Impedance Control

In this paper, a comparison analysis between geometric impedance controls (GICs) derived from two different potential functions on SE(3) for robotic manipulators is presented. The first potential function is defined on the Lie group, utilizing the Frobenius norm of the configuration error matrix. The second potential function is defined utilizing the Lie algebra, i.e., log-map of the configuration error. Using a differential geometric approach, the detailed derivation of the distance metric and potential function on SE(3) is introduced. The GIC laws are respectively derived from the two potential functions, followed by extensive comparison analyses. In the qualitative analysis, the properties of the error function and control laws are analyzed, while the performances of the controllers are quantitatively compared using numerical simulation.

Clustering Techniques for Stable Linear Dynamical Systems with applications to Hard Disk Drives

In Robust Control and Data Driven Robust Control design methodologies, multiple plant transfer functions or a family of transfer functions are considered and a common controller is designed such that all the plants that fall into this family are stabilized. Though the plants are stabilized, the controller might be sub-optimal for each of the plants when the variations in the plants are large. This paper presents a way of clustering stable linear dynamical systems for the design of robust controllers within each of the clusters such that the controllers are optimal for each of the clusters. First a k-medoids algorithm for hard clustering will be presented for stable Linear Time Invariant (LTI) systems and then a Gaussian Mixture Models (GMM) clustering for a special class of LTI systems, common for Hard Disk Drive plants, will be presented.

Robot Manipulation Task Learning by Leveraging SE(3) Group Invariance and Equivariance

This paper presents a differential geometric control approach that leverages SE(3) group invariance and equivariance to increase transferability in learning robot manipulation tasks that involve interaction with the environment. Specifically, we employ a control law and a learning representation framework that remain invariant under arbitrary SE(3) transformations of the manipulation task definition. Furthermore, the control law and learning representation framework are shown to be SE(3) equivariant when represented relative to the spatial frame. The proposed approach is based on utilizing a recently presented geometric impedance control (GIC) combined with a learning variable impedance control framework, where the gain scheduling policy is trained in a supervised learning fashion from expert demonstrations. A geometrically consistent error vector (GCEV) is fed to a neural network to achieve a gain scheduling policy that remains invariant to arbitrary translation and rotations. A comparison of our proposed control and learning framework with a well-known Cartesian space learning impedance control, equipped with a Cartesian error vector-based gain scheduling policy, confirms the significantly superior learning transferability of our proposed approach. A hardware implementation on a peg-in-hole task is conducted to validate the learning transferability and feasibility of the proposed approach.

Geometric Impedance Control on SE for Robotic Manipulators

After its introduction, impedance control has been utilized as a primary control scheme for robotic manipulation tasks that involve interaction with unknown environments. While impedance control has been extensively studied, the geometric structure of SE(3) for the robotic manipulator itself and its use in formulating a robotic task has not been adequately addressed. In this paper, we propose a differential geometric approach to impedance control. Given a left-invariant error metric in SE(3), the corresponding error vectors in position and velocity are first derived. Using these geometrically consistent error vectors, we propose a novel impedance control scheme, which adequately accounts for the geometric structure of the manipulator in SE(3). The closed-loop stability for the proposed control schemes is verified using a Lyapunov function-based analysis. The proposed control design clearly outperformed a conventional impedance control approach when tracking challenging trajectory profiles.

Adaptive Model Predictive Control of Wheeled Mobile Robots

In this paper, a control algorithm for guiding a two wheeled mobile robot with unknown inertia to a desired point and orientation using an Adaptive Model Predictive Control (AMPC) framework is presented. The two wheeled mobile robot is modeled as a knife edge or a skate with nonholonomic kinematic constraints and the dynamical equations are derived using the Lagrangian approach. The inputs at every time instant are obtained from Model Predictive Control (MPC) with a set of nominal parameters which are updated using a recursive least squares algorithm. The efficacy of the algorithm is demonstrated through numerical simulations at the end of the paper.

Nonlinear control of a swinging pendulum on a wheeled mobile robot with nonholonomic constraints

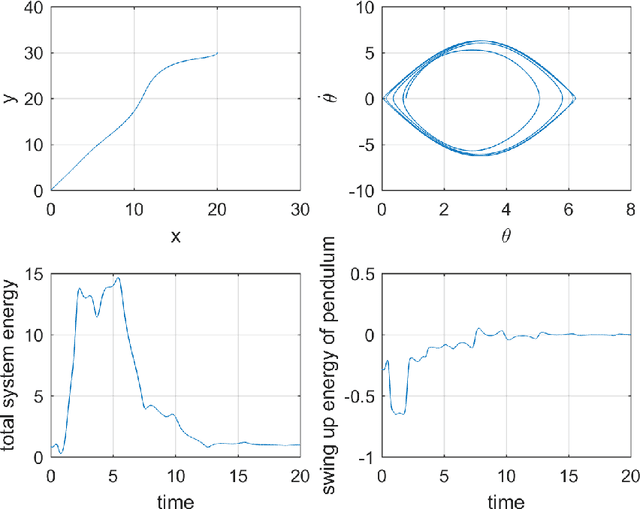
In this paper, we propose a nonlinear control strategy for swinging up a pendulum to its upright equilibrium position by shaping its swinging energy along with regulating the cart to a desired location. While the base of a usual cart-pole system is restricted to move in a straight line, the present system is allowed to move in the x-y plane with a nonholonomic consraint that its allowable velocity is only along its orientation. A simple time invariant control law has been presented and its effectiveness has been demonstrated using numerical experiments.