Sparse Contrastive Learning for Content-Based Cold Item Recommendation

Item cold-start is a pervasive challenge for collaborative filtering (CF) recommender systems. Existing methods often train cold-start models by mapping auxiliary item content, such as images or text descriptions, into the embedding space of a CF model. However, such approaches can be limited by the fundamental information gap between CF signals and content features. In this work, we propose to avoid this limitation with purely content-based modeling of cold items, i.e. without alignment with CF user or item embeddings. We instead frame cold-start prediction in terms of item-item similarity, training a content encoder to project into a latent space where similarity correlates with user preferences. We define our training objective as a sparse generalization of sampled softmax loss with the $α$-entmax family of activation functions, which allows for sharper estimation of item relevance by zeroing gradients for uninformative negatives. We then describe how this Sampled Entmax for Cold-start (SEMCo) training regime can be extended via knowledge distillation, and show that it outperforms existing cold-start methods and standard sampled softmax in ranking accuracy. We also discuss the advantages of purely content-based modeling, particularly in terms of equity of item outcomes.

Leveraging Artist Catalogs for Cold-Start Music Recommendation

The item cold-start problem poses a fundamental challenge for music recommendation: newly added tracks lack the interaction history that collaborative filtering (CF) requires. Existing approaches often address this problem by learning mappings from content features such as audio, text, and metadata to the CF latent space. However, previous works either omit artist information or treat it as just another input modality, missing the fundamental hierarchy of artists and items. Since most new tracks come from artists with previous history available, we frame cold-start track recommendation as 'semi-cold' by leveraging the rich collaborative signal that exists at the artist level. We show that artist-aware methods can more than double Recall and NDCG compared to content-only baselines, and propose ACARec, an attention-based architecture that generates CF embeddings for new tracks by attending over the artist's existing catalog. We show that our approach has notable advantages in predicting user preferences for new tracks, especially for new artist discovery and more accurate estimation of cold item popularity.

Towards Effective Negation Modeling in Joint Audio-Text Models for Music

Joint audio-text models are widely used for music retrieval, yet they struggle with semantic phenomena such as negation. Negation is fundamental for distinguishing the absence (or presence) of musical elements (e.g., "with vocals" vs. "without vocals"), but current systems fail to represent this reliably. In this work, we investigate and mitigate this limitation by training CLAP models from scratch on the Million Song Dataset with LP-MusicCaps-MSD captions. We introduce negation through text augmentation and a dissimilarity-based contrastive loss, designed to explicitly separate original and negated captions in the joint embedding space. To evaluate progress, we propose two protocols that frame negation modeling as retrieval and binary classification tasks. Experiments demonstrate that both methods, individually and combined, improve negation handling while largely preserving retrieval performance.

Towards a Unified Representation Evaluation Framework Beyond Downstream Tasks

Downstream probing has been the dominant method for evaluating model representations, an important process given the increasing prominence of self-supervised learning and foundation models. However, downstream probing primarily assesses the availability of task-relevant information in the model's latent space, overlooking attributes such as equivariance, invariance, and disentanglement, which contribute to the interpretability, adaptability, and utility of representations in real-world applications. While some attempts have been made to measure these qualities in representations, no unified evaluation framework with modular, generalizable, and interpretable metrics exists. In this paper, we argue for the importance of representation evaluation beyond downstream probing. We introduce a standardized protocol to quantify informativeness, equivariance, invariance, and disentanglement of factors of variation in model representations. We use it to evaluate representations from a variety of models in the image and speech domains using different architectures and pretraining approaches on identified controllable factors of variation. We find that representations from models with similar downstream performance can behave substantially differently with regard to these attributes. This hints that the respective mechanisms underlying their downstream performance are functionally different, prompting new research directions to understand and improve representations.

Learning Music Audio Representations With Limited Data

Large deep-learning models for music, including those focused on learning general-purpose music audio representations, are often assumed to require substantial training data to achieve high performance. If true, this would pose challenges in scenarios where audio data or annotations are scarce, such as for underrepresented music traditions, non-popular genres, and personalized music creation and listening. Understanding how these models behave in limited-data scenarios could be crucial for developing techniques to tackle them. In this work, we investigate the behavior of several music audio representation models under limited-data learning regimes. We consider music models with various architectures, training paradigms, and input durations, and train them on data collections ranging from 5 to 8,000 minutes long. We evaluate the learned representations on various music information retrieval tasks and analyze their robustness to noise. We show that, under certain conditions, representations from limited-data and even random models perform comparably to ones from large-dataset models, though handcrafted features outperform all learned representations in some tasks.

Evaluation of pretrained language models on music understanding

Music-text multimodal systems have enabled new approaches to Music Information Research (MIR) applications such as audio-to-text and text-to-audio retrieval, text-based song generation, and music captioning. Despite the reported success, little effort has been put into evaluating the musical knowledge of Large Language Models (LLM). In this paper, we demonstrate that LLMs suffer from 1) prompt sensitivity, 2) inability to model negation (e.g. 'rock song without guitar'), and 3) sensitivity towards the presence of specific words. We quantified these properties as a triplet-based accuracy, evaluating the ability to model the relative similarity of labels in a hierarchical ontology. We leveraged the Audioset ontology to generate triplets consisting of an anchor, a positive (relevant) label, and a negative (less relevant) label for the genre and instruments sub-tree. We evaluated the triplet-based musical knowledge for six general-purpose Transformer-based models. The triplets obtained through this methodology required filtering, as some were difficult to judge and therefore relatively uninformative for evaluation purposes. Despite the relatively high accuracy reported, inconsistencies are evident in all six models, suggesting that off-the-shelf LLMs need adaptation to music before use.

I can listen but cannot read: An evaluation of two-tower multimodal systems for instrument recognition

Music two-tower multimodal systems integrate audio and text modalities into a joint audio-text space, enabling direct comparison between songs and their corresponding labels. These systems enable new approaches for classification and retrieval, leveraging both modalities. Despite the promising results they have shown for zero-shot classification and retrieval tasks, closer inspection of the embeddings is needed. This paper evaluates the inherent zero-shot properties of joint audio-text spaces for the case-study of instrument recognition. We present an evaluation and analysis of two-tower systems for zero-shot instrument recognition and a detailed analysis of the properties of the pre-joint and joint embeddings spaces. Our findings suggest that audio encoders alone demonstrate good quality, while challenges remain within the text encoder or joint space projection. Specifically, two-tower systems exhibit sensitivity towards specific words, favoring generic prompts over musically informed ones. Despite the large size of textual encoders, they do not yet leverage additional textual context or infer instruments accurately from their descriptions. Lastly, a novel approach for quantifying the semantic meaningfulness of the textual space leveraging an instrument ontology is proposed. This method reveals deficiencies in the systems' understanding of instruments and provides evidence of the need for fine-tuning text encoders on musical data.

Time-of-arrival Estimation and Phase Unwrapping of Head-related Transfer Functions With Integer Linear Programming

In binaural audio synthesis, aligning head-related impulse responses (HRIRs) in time has been an important pre-processing step, enabling accurate spatial interpolation and efficient data compression. The maximum correlation time delay between spatially nearby HRIRs has previously been used to get accurate and smooth alignment by solving a matrix equation in which the solution has the minimum Euclidean distance to the time delay. However, the Euclidean criterion could lead to an over-smoothing solution in practice. In this paper, we solve the smoothing issue by formulating the task as solving an integer linear programming problem equivalent to minimising an $L^1$-norm. Moreover, we incorporate 1) the cross-correlation of inter-aural HRIRs, and 2) HRIRs with their minimum-phase responses to have more reference measurements for optimisation. We show the proposed method can get more accurate alignments than the Euclidean-based method by comparing the spectral reconstruction loss of time-aligned HRIRs using spherical harmonics representation on seven HRIRs consisting of human and dummy heads. The extra correlation features and the $L^1$-norm are also beneficial in extremely noisy conditions. In addition, this method can be applied to phase unwrapping of head-related transfer functions, where the unwrapped phase could be a compact feature for downstream tasks.

On The Relevance Of The Differences Between HRTF Measurement Setups For Machine Learning

As spatial audio is enjoying a surge in popularity, data-driven machine learning techniques that have been proven successful in other domains are increasingly used to process head-related transfer function measurements. However, these techniques require much data, whereas the existing datasets are ranging from tens to the low hundreds of datapoints. It therefore becomes attractive to combine multiple of these datasets, although they are measured under different conditions. In this paper, we first establish the common ground between a number of datasets, then we investigate potential pitfalls of mixing datasets. We perform a simple experiment to test the relevance of the remaining differences between datasets when applying machine learning techniques. Finally, we pinpoint the most relevant differences.

A Critical Look at the Applicability of Markov Logic Networks for Music Signal Analysis

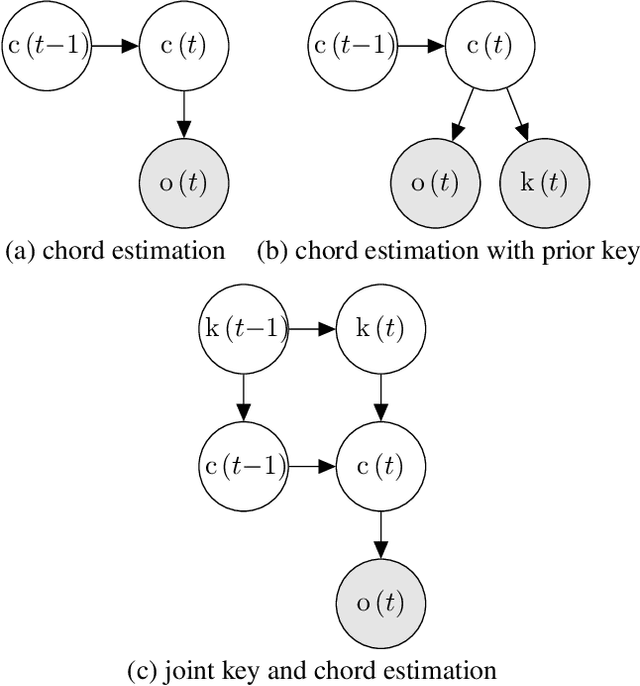
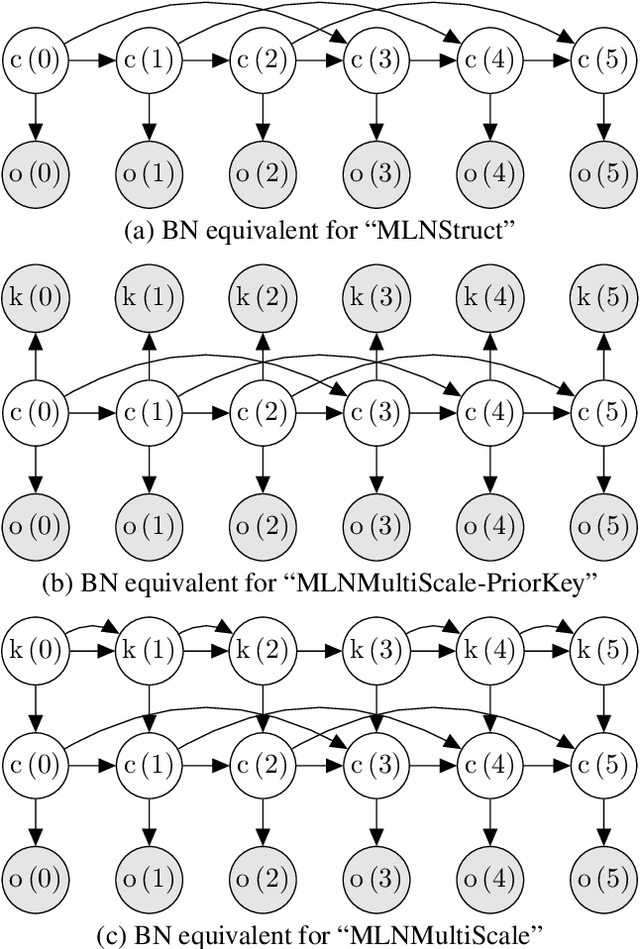
In recent years, Markov logic networks (MLNs) have been proposed as a potentially useful paradigm for music signal analysis. Because all hidden Markov models can be reformulated as MLNs, the latter can provide an all-encompassing framework that reuses and extends previous work in the field. However, just because it is theoretically possible to reformulate previous work as MLNs, does not mean that it is advantageous. In this paper, we analyse some proposed examples of MLNs for musical analysis and consider their practical disadvantages when compared to formulating the same musical dependence relationships as (dynamic) Bayesian networks. We argue that a number of practical hurdles such as the lack of support for sequences and for arbitrary continuous probability distributions make MLNs less than ideal for the proposed musical applications, both in terms of easy of formulation and computational requirements due to their required inference algorithms. These conclusions are not specific to music, but apply to other fields as well, especially when sequential data with continuous observations is involved. Finally, we show that the ideas underlying the proposed examples can be expressed perfectly well in the more commonly used framework of (dynamic) Bayesian networks.