Multi-Cycle-Consistent Adversarial Networks for Edge Denoising of Computed Tomography Images

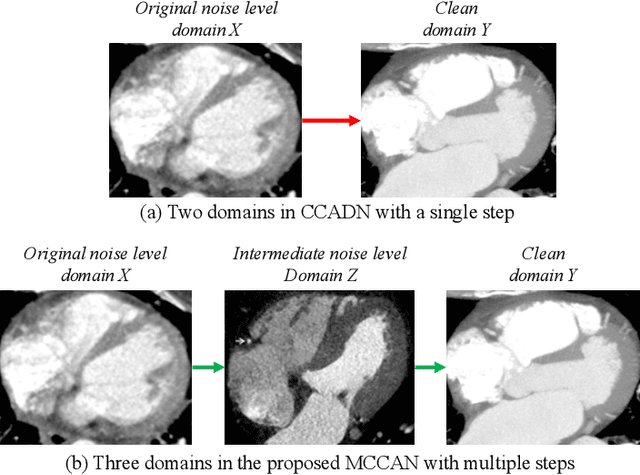
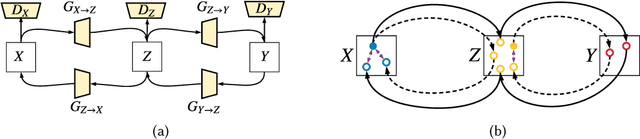
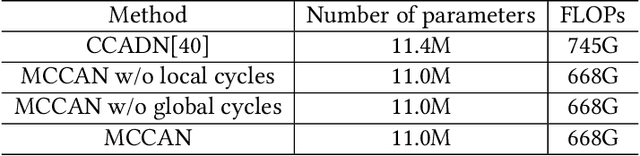
As one of the most commonly ordered imaging tests, computed tomography (CT) scan comes with inevitable radiation exposure that increases the cancer risk to patients. However, CT image quality is directly related to radiation dose, thus it is desirable to obtain high-quality CT images with as little dose as possible. CT image denoising tries to obtain high dose like high-quality CT images (domain X) from low dose low-quality CTimages (domain Y), which can be treated as an image-to-image translation task where the goal is to learn the transform between a source domain X (noisy images) and a target domain Y (clean images). In this paper, we propose a multi-cycle-consistent adversarial network (MCCAN) that builds intermediate domains and enforces both local and global cycle-consistency for edge denoising of CT images. The global cycle-consistency couples all generators together to model the whole denoising process, while the local cycle-consistency imposes effective supervision on the process between adjacent domains. Experiments show that both local and global cycle-consistency are important for the success of MCCAN, which outperformsCCADN in terms of denoising quality with slightly less computation resource consumption.

Multi-Cycle-Consistent Adversarial Networks for CT Image Denoising

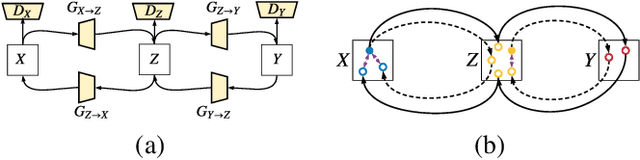
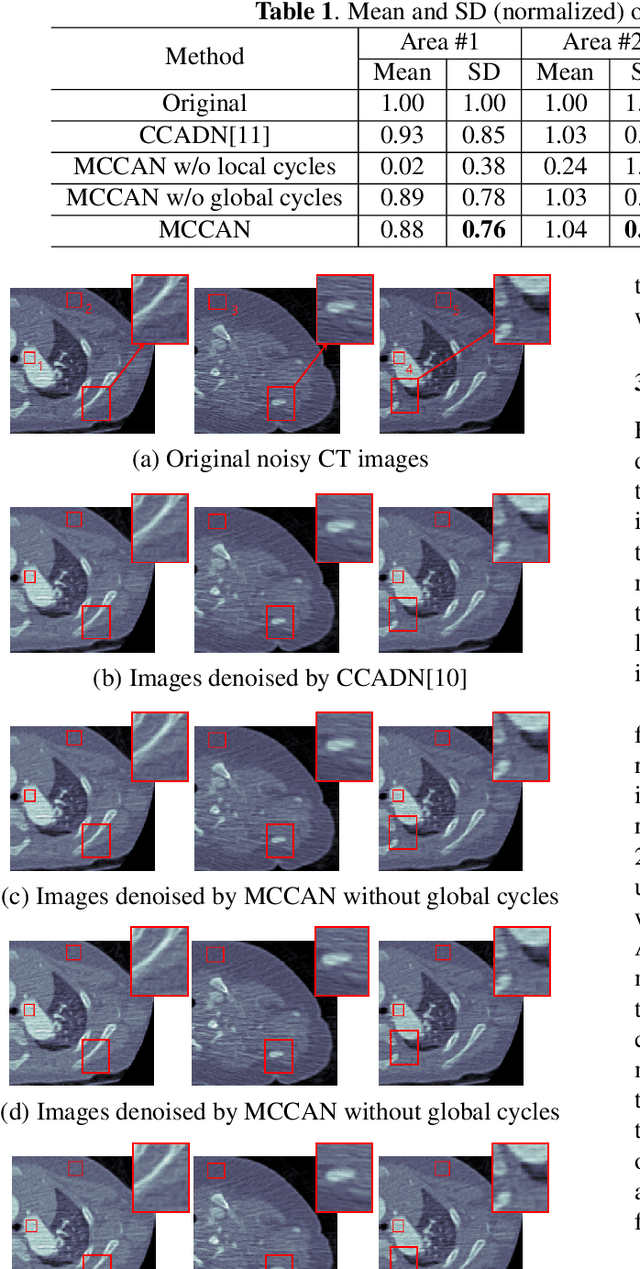
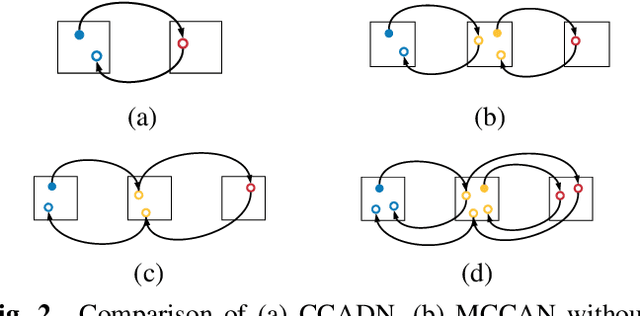
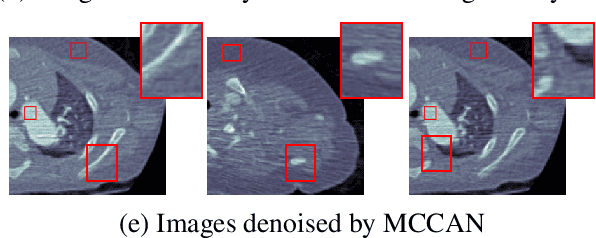
CT image denoising can be treated as an image-to-image translation task where the goal is to learn the transform between a source domain $X$ (noisy images) and a target domain $Y$ (clean images). Recently, cycle-consistent adversarial denoising network (CCADN) has achieved state-of-the-art results by enforcing cycle-consistent loss without the need of paired training data. Our detailed analysis of CCADN raises a number of interesting questions. For example, if the noise is large leading to significant difference between domain $X$ and domain $Y$, can we bridge $X$ and $Y$ with an intermediate domain $Z$ such that both the denoising process between $X$ and $Z$ and that between $Z$ and $Y$ are easier to learn? As such intermediate domains lead to multiple cycles, how do we best enforce cycle-consistency? Driven by these questions, we propose a multi-cycle-consistent adversarial network (MCCAN) that builds intermediate domains and enforces both local and global cycle-consistency. The global cycle-consistency couples all generators together to model the whole denoising process, while the local cycle-consistency imposes effective supervision on the process between adjacent domains. Experiments show that both local and global cycle-consistency are important for the success of MCCAN, which outperforms the state-of-the-art.

Evaluation of Neural Network Uncertainty Estimation with Application to Resource-Constrained Platforms

The ability to accurately estimate uncertainties in neural network predictions is of great importance in many critical tasks. In this paper, we first analyze the intrinsic relation between two main use cases of uncertainty estimation, i.e., selective prediction and confidence calibration. We then reveal the potential issues with the existing quality metrics for uncertainty estimation and propose new metrics to mitigate them. Finally, we apply these new metrics to resource-constrained platforms such as autonomous driver assistance systems where the quality of uncertainty estimation is critical. By exploring the trade-off between the model size and the estimation quality, a missing piece in the literature, some interesting trends are observed.

On the Universal Approximability and Complexity Bounds of Quantized ReLU Neural Networks

Compression is a key step to deploy large neural networks on resource-constrained platforms. As a popular compression technique, quantization constrains the number of distinct weight values and thus reducing the number of bits required to represent and store each weight. In this paper, we study the representation power of quantized neural networks. First, we prove the universal approximability of quantized ReLU networks on a wide class of functions. Then we provide upper bounds on the number of weights and the memory size for a given approximation error bound and the bit-width of weights for function-independent and function-dependent structures. Our results reveal that, to attain an approximation error bound of $\epsilon$, the number of weights needed by a quantized network is no more than $\mathcal{O}\left(\log^5(1/\epsilon)\right)$ times that of an unquantized network. This overhead is of much lower order than the lower bound of the number of weights needed for the error bound, supporting the empirical success of various quantization techniques. To the best of our knowledge, this is the first in-depth study on the complexity bounds of quantized neural networks.

PBGen: Partial Binarization of Deconvolution-Based Generators for Edge Intelligence

This work explores the binarization of the deconvolution-based generator in a GAN for memory saving and speedup of image construction. Our study suggests that different from convolutional neural networks (including the discriminator) where all layers can be binarized, only some of the layers in the generator can be binarized without significant performance loss. Supported by theoretical analysis and verified by experiments, a direct metric based on the dimension of deconvolution operations is established, which can be used to quickly decide which layers in the generator can be binarized. Our results also indicate that both the generator and the discriminator should be binarized simultaneously for balanced competition and better performance. Experimental results based on CelebA suggest that directly applying state-of-the-art binarization techniques to all the layers of the generator will lead to 2.83$\times$ performance loss measured by sliced Wasserstein distance compared with the original generator, while applying them to selected layers only can yield up to 25.81$\times$ saving in memory consumption, and 1.96$\times$ and 1.32$\times$ speedup in inference and training respectively with little performance loss.