Optimal Projection for 3D Gaussian Splatting

3D Gaussian Splatting has garnered extensive attention and application in real-time neural rendering. Concurrently, concerns have been raised about the limitations of this technology in aspects such as point cloud storage, performance , and robustness in sparse viewpoints , leading to various improvements. However, there has been a notable lack of attention to the projection errors introduced by the local affine approximation inherent in the splatting itself, and the consequential impact of these errors on the quality of photo-realistic rendering. This paper addresses the projection error function of 3D Gaussian Splatting, commencing with the residual error from the first-order Taylor expansion of the projection function $\phi$. The analysis establishes a correlation between the error and the Gaussian mean position. Subsequently, leveraging function optimization theory, this paper analyzes the function's minima to provide an optimal projection strategy for Gaussian Splatting referred to Optimal Gaussian Splatting. Experimental validation further confirms that this projection methodology reduces artifacts, resulting in a more convincingly realistic rendering.

360-GS: Layout-guided Panoramic Gaussian Splatting For Indoor Roaming

3D Gaussian Splatting (3D-GS) has recently attracted great attention with real-time and photo-realistic renderings. This technique typically takes perspective images as input and optimizes a set of 3D elliptical Gaussians by splatting them onto the image planes, resulting in 2D Gaussians. However, applying 3D-GS to panoramic inputs presents challenges in effectively modeling the projection onto the spherical surface of ${360^\circ}$ images using 2D Gaussians. In practical applications, input panoramas are often sparse, leading to unreliable initialization of 3D Gaussians and subsequent degradation of 3D-GS quality. In addition, due to the under-constrained geometry of texture-less planes (e.g., walls and floors), 3D-GS struggles to model these flat regions with elliptical Gaussians, resulting in significant floaters in novel views. To address these issues, we propose 360-GS, a novel $360^{\circ}$ Gaussian splatting for a limited set of panoramic inputs. Instead of splatting 3D Gaussians directly onto the spherical surface, 360-GS projects them onto the tangent plane of the unit sphere and then maps them to the spherical projections. This adaptation enables the representation of the projection using Gaussians. We guide the optimization of 360-GS by exploiting layout priors within panoramas, which are simple to obtain and contain strong structural information about the indoor scene. Our experimental results demonstrate that 360-GS allows panoramic rendering and outperforms state-of-the-art methods with fewer artifacts in novel view synthesis, thus providing immersive roaming in indoor scenarios.

Local-to-Global Panorama Inpainting for Locale-Aware Indoor Lighting Prediction

Predicting panoramic indoor lighting from a single perspective image is a fundamental but highly ill-posed problem in computer vision and graphics. To achieve locale-aware and robust prediction, this problem can be decomposed into three sub-tasks: depth-based image warping, panorama inpainting and high-dynamic-range (HDR) reconstruction, among which the success of panorama inpainting plays a key role. Recent methods mostly rely on convolutional neural networks (CNNs) to fill the missing contents in the warped panorama. However, they usually achieve suboptimal performance since the missing contents occupy a very large portion in the panoramic space while CNNs are plagued by limited receptive fields. The spatially-varying distortion in the spherical signals further increases the difficulty for conventional CNNs. To address these issues, we propose a local-to-global strategy for large-scale panorama inpainting. In our method, a depth-guided local inpainting is first applied on the warped panorama to fill small but dense holes. Then, a transformer-based network, dubbed PanoTransformer, is designed to hallucinate reasonable global structures in the large holes. To avoid distortion, we further employ cubemap projection in our design of PanoTransformer. The high-quality panorama recovered at any locale helps us to capture spatially-varying indoor illumination with physically-plausible global structures and fine details.

Self-NeRF: A Self-Training Pipeline for Few-Shot Neural Radiance Fields

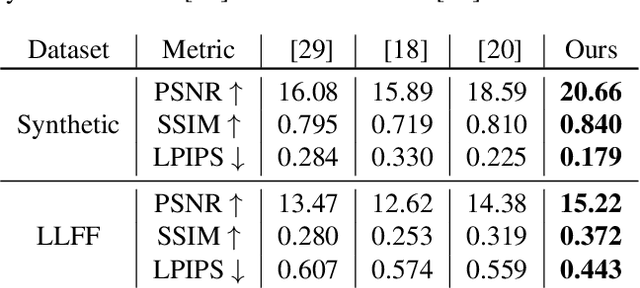
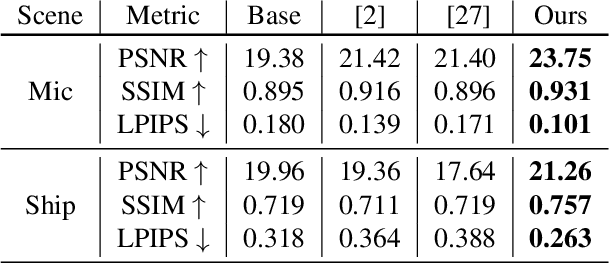
Recently, Neural Radiance Fields (NeRF) have emerged as a potent method for synthesizing novel views from a dense set of images. Despite its impressive performance, NeRF is plagued by its necessity for numerous calibrated views and its accuracy diminishes significantly in a few-shot setting. To address this challenge, we propose Self-NeRF, a self-evolved NeRF that iteratively refines the radiance fields with very few number of input views, without incorporating additional priors. Basically, we train our model under the supervision of reference and unseen views simultaneously in an iterative procedure. In each iteration, we label unseen views with the predicted colors or warped pixels generated by the model from the preceding iteration. However, these expanded pseudo-views are afflicted by imprecision in color and warping artifacts, which degrades the performance of NeRF. To alleviate this issue, we construct an uncertainty-aware NeRF with specialized embeddings. Some techniques such as cone entropy regularization are further utilized to leverage the pseudo-views in the most efficient manner. Through experiments under various settings, we verified that our Self-NeRF is robust to input with uncertainty and surpasses existing methods when trained on limited training data.

Deep Graph Learning for Spatially-Varying Indoor Lighting Prediction

Lighting prediction from a single image is becoming increasingly important in many vision and augmented reality (AR) applications in which shading and shadow consistency between virtual and real objects should be guaranteed. However, this is a notoriously ill-posed problem, especially for indoor scenarios, because of the complexity of indoor luminaires and the limited information involved in 2D images. In this paper, we propose a graph learning-based framework for indoor lighting estimation. At its core is a new lighting model (dubbed DSGLight) based on depth-augmented Spherical Gaussians (SG) and a Graph Convolutional Network (GCN) that infers the new lighting representation from a single LDR image of limited field-of-view. Our lighting model builds 128 evenly distributed SGs over the indoor panorama, where each SG encoding the lighting and the depth around that node. The proposed GCN then learns the mapping from the input image to DSGLight. Compared with existing lighting models, our DSGLight encodes both direct lighting and indirect environmental lighting more faithfully and compactly. It also makes network training and inference more stable. The estimated depth distribution enables temporally stable shading and shadows under spatially-varying lighting. Through thorough experiments, we show that our method obviously outperforms existing methods both qualitatively and quantitatively.

GLPanoDepth: Global-to-Local Panoramic Depth Estimation

In this paper, we propose a learning-based method for predicting dense depth values of a scene from a monocular omnidirectional image. An omnidirectional image has a full field-of-view, providing much more complete descriptions of the scene than perspective images. However, fully-convolutional networks that most current solutions rely on fail to capture rich global contexts from the panorama. To address this issue and also the distortion of equirectangular projection in the panorama, we propose Cubemap Vision Transformers (CViT), a new transformer-based architecture that can model long-range dependencies and extract distortion-free global features from the panorama. We show that cubemap vision transformers have a global receptive field at every stage and can provide globally coherent predictions for spherical signals. To preserve important local features, we further design a convolution-based branch in our pipeline (dubbed GLPanoDepth) and fuse global features from cubemap vision transformers at multiple scales. This global-to-local strategy allows us to fully exploit useful global and local features in the panorama, achieving state-of-the-art performance in panoramic depth estimation.