Jiaxu Cui
Symbolic Foundation Regressor on Complex Networks
May 28, 2025Abstract:In science, we are interested not only in forecasting but also in understanding how predictions are made, specifically what the interpretable underlying model looks like. Data-driven machine learning technology can significantly streamline the complex and time-consuming traditional manual process of discovering scientific laws, helping us gain insights into fundamental issues in modern science. In this work, we introduce a pre-trained symbolic foundation regressor that can effectively compress complex data with numerous interacting variables while producing interpretable physical representations. Our model has been rigorously tested on non-network symbolic regression, symbolic regression on complex networks, and the inference of network dynamics across various domains, including physics, biochemistry, ecology, and epidemiology. The results indicate a remarkable improvement in equation inference efficiency, being three times more effective than baseline approaches while maintaining accurate predictions. Furthermore, we apply our model to uncover more intuitive laws of interaction transmission from global epidemic outbreak data, achieving optimal data fitting. This model extends the application boundary of pre-trained symbolic regression models to complex networks, and we believe it provides a foundational solution for revealing the hidden mechanisms behind changes in complex phenomena, enhancing interpretability, and inspiring further scientific discoveries.
scSiameseClu: A Siamese Clustering Framework for Interpreting single-cell RNA Sequencing Data
May 19, 2025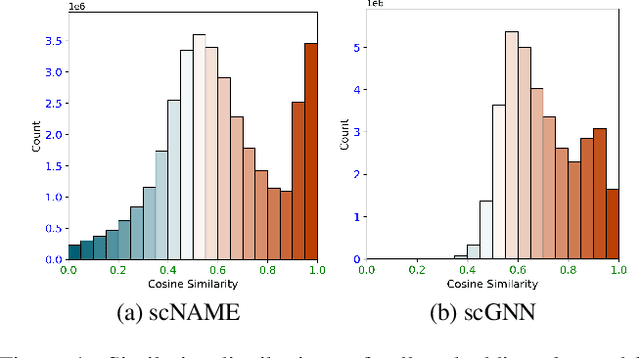
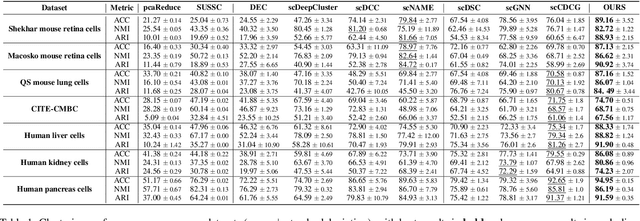
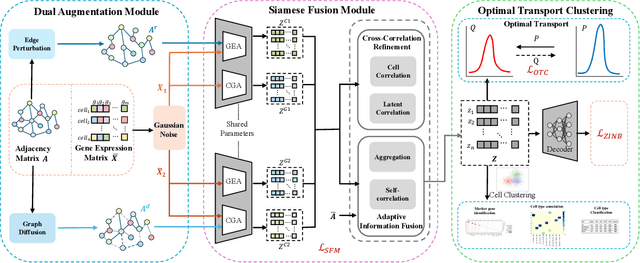
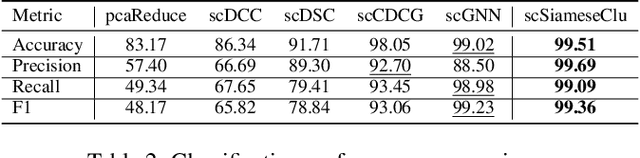
Abstract:Single-cell RNA sequencing (scRNA-seq) reveals cell heterogeneity, with cell clustering playing a key role in identifying cell types and marker genes. Recent advances, especially graph neural networks (GNNs)-based methods, have significantly improved clustering performance. However, the analysis of scRNA-seq data remains challenging due to noise, sparsity, and high dimensionality. Compounding these challenges, GNNs often suffer from over-smoothing, limiting their ability to capture complex biological information. In response, we propose scSiameseClu, a novel Siamese Clustering framework for interpreting single-cell RNA-seq data, comprising of 3 key steps: (1) Dual Augmentation Module, which applies biologically informed perturbations to the gene expression matrix and cell graph relationships to enhance representation robustness; (2) Siamese Fusion Module, which combines cross-correlation refinement and adaptive information fusion to capture complex cellular relationships while mitigating over-smoothing; and (3) Optimal Transport Clustering, which utilizes Sinkhorn distance to efficiently align cluster assignments with predefined proportions while maintaining balance. Comprehensive evaluations on seven real-world datasets demonstrate that~\methodname~outperforms state-of-the-art methods in single-cell clustering, cell type annotation, and cell type classification, providing a powerful tool for scRNA-seq data interpretation.
Learning Interpretable Network Dynamics via Universal Neural Symbolic Regression
Nov 11, 2024Abstract:Discovering governing equations of complex network dynamics is a fundamental challenge in contemporary science with rich data, which can uncover the mysterious patterns and mechanisms of the formation and evolution of complex phenomena in various fields and assist in decision-making. In this work, we develop a universal computational tool that can automatically, efficiently, and accurately learn the symbolic changing patterns of complex system states by combining the excellent fitting ability from deep learning and the equation inference ability from pre-trained symbolic regression. We conduct intensive experimental verifications on more than ten representative scenarios from physics, biochemistry, ecology, epidemiology, etc. Results demonstrate the outstanding effectiveness and efficiency of our tool by comparing with the state-of-the-art symbolic regression techniques for network dynamics. The application to real-world systems including global epidemic transmission and pedestrian movements has verified its practical applicability. We believe that our tool can serve as a universal solution to dispel the fog of hidden mechanisms of changes in complex phenomena, advance toward interpretability, and inspire more scientific discoveries.
Learning Continuous Network Emerging Dynamics from Scarce Observations via Data-Adaptive Stochastic Processes
Oct 25, 2023Abstract:Learning network dynamics from the empirical structure and spatio-temporal observation data is crucial to revealing the interaction mechanisms of complex networks in a wide range of domains. However, most existing methods only aim at learning network dynamic behaviors generated by a specific ordinary differential equation instance, resulting in ineffectiveness for new ones, and generally require dense observations. The observed data, especially from network emerging dynamics, are usually difficult to obtain, which brings trouble to model learning. Therefore, how to learn accurate network dynamics with sparse, irregularly-sampled, partial, and noisy observations remains a fundamental challenge. We introduce Neural ODE Processes for Network Dynamics (NDP4ND), a new class of stochastic processes governed by stochastic data-adaptive network dynamics, to overcome the challenge and learn continuous network dynamics from scarce observations. Intensive experiments conducted on various network dynamics in ecological population evolution, phototaxis movement, brain activity, epidemic spreading, and real-world empirical systems, demonstrate that the proposed method has excellent data adaptability and computational efficiency, and can adapt to unseen network emerging dynamics, producing accurate interpolation and extrapolation with reducing the ratio of required observation data to only about 6\% and improving the learning speed for new dynamics by three orders of magnitude.
Deep Bayesian Optimization on Attributed Graphs
May 31, 2019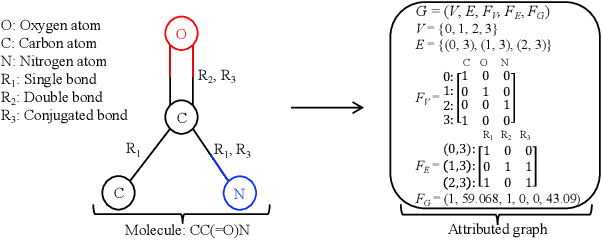

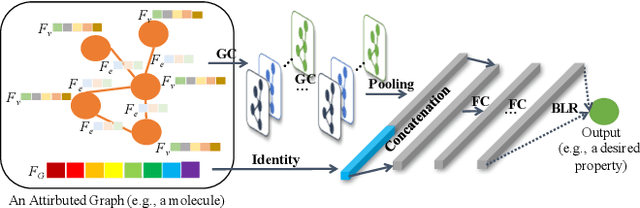

Abstract:Attributed graphs, which contain rich contextual features beyond just network structure, are ubiquitous and have been observed to benefit various network analytics applications. Graph structure optimization, aiming to find the optimal graphs in terms of some specific measures, has become an effective computational tool in complex network analysis. However, traditional model-free methods suffer from the expensive computational cost of evaluating graphs; existing vectorial Bayesian optimization methods cannot be directly applied to attributed graphs and have the scalability issue due to the use of Gaussian processes (GPs). To bridge the gap, in this paper, we propose a novel scalable Deep Graph Bayesian Optimization (DGBO) method on attributed graphs. The proposed DGBO prevents the cubical complexity of the GPs by adopting a deep graph neural network to surrogate black-box functions, and can scale linearly with the number of observations. Intensive experiments are conducted on both artificial and real-world problems, including molecular discovery and urban road network design, and demonstrate the effectiveness of the DGBO compared with the state-of-the-art.
Learning Optimal Data Augmentation Policies via Bayesian Optimization for Image Classification Tasks
May 23, 2019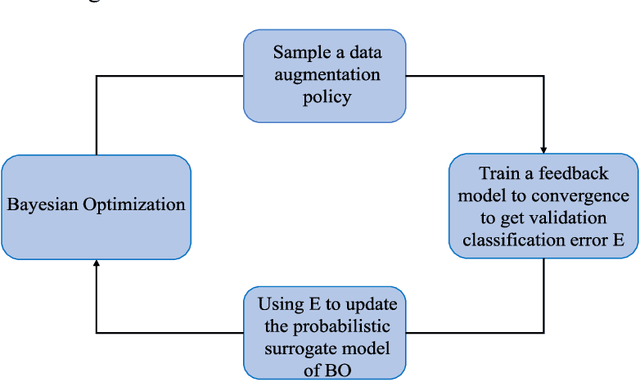
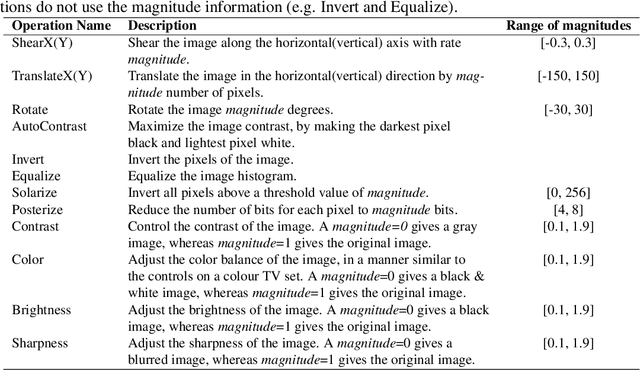

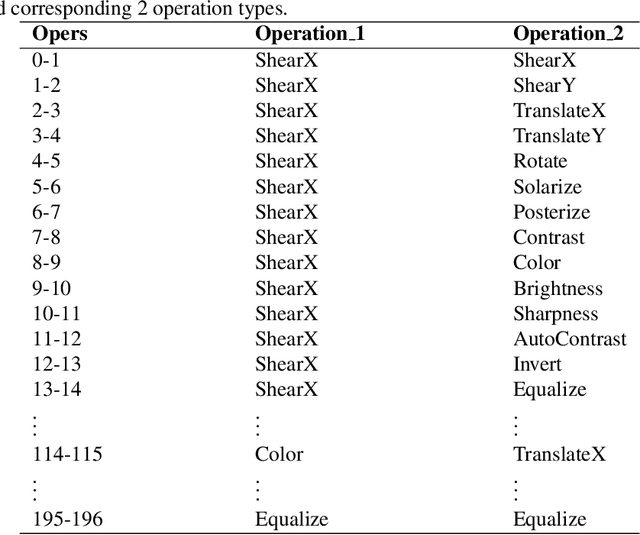
Abstract:In recent years, deep learning has achieved remarkable achievements in many fields, including computer vision, natural language processing, speech recognition and others. Adequate training data is the key to ensure the effectiveness of the deep models. However, obtaining valid data requires a lot of time and labor resources. Data augmentation (DA) is an effective alternative approach, which can generate new labeled data based on existing data using label-preserving transformations. Although we can benefit a lot from DA, designing appropriate DA policies requires a lot of expert experience and time consumption, and the evaluation of searching the optimal policies is costly. So we raise a new question in this paper: how to achieve automated data augmentation at as low cost as possible? We propose a method named BO-Aug for automating the process by finding the optimal DA policies using the Bayesian optimization approach. Our method can find the optimal policies at a relatively low search cost, and the searched policies based on a specific dataset are transferable across different neural network architectures or even different datasets. We validate the BO-Aug on three widely used image classification datasets, including CIFAR-10, CIFAR-100 and SVHN. Experimental results show that the proposed method can achieve state-of-the-art or near advanced classification accuracy. Code to reproduce our experiments is available at https://github.com/zhangxiaozao/BO-Aug.
Deep Neural Architecture Search with Deep Graph Bayesian Optimization
May 14, 2019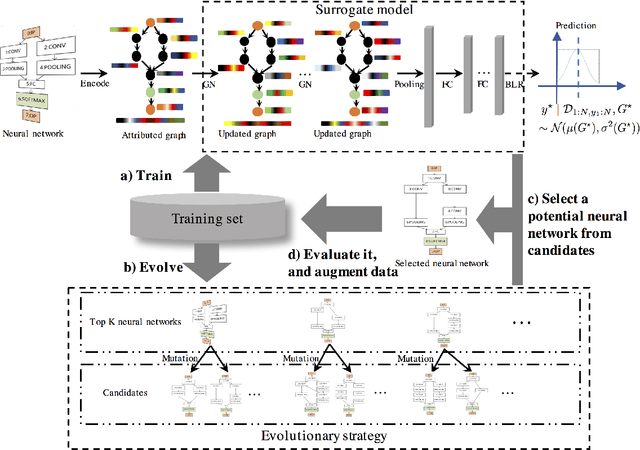

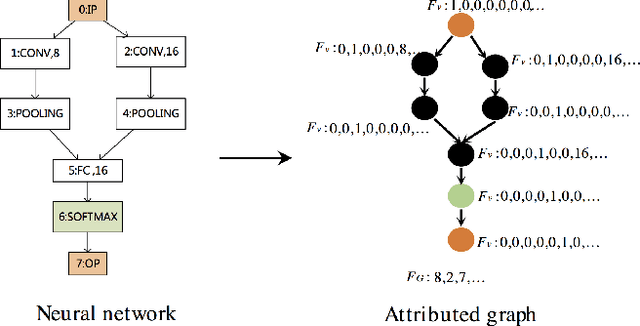
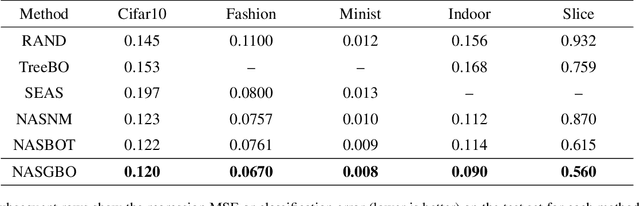
Abstract:Bayesian optimization (BO) is an effective method of finding the global optima of black-box functions. Recently BO has been applied to neural architecture search and shows better performance than pure evolutionary strategies. All these methods adopt Gaussian processes (GPs) as surrogate function, with the handcraft similarity metrics as input. In this work, we propose a Bayesian graph neural network as a new surrogate, which can automatically extract features from deep neural architectures, and use such learned features to fit and characterize black-box objectives and their uncertainty. Based on the new surrogate, we then develop a graph Bayesian optimization framework to address the challenging task of deep neural architecture search. Experiment results show our method significantly outperforms the comparative methods on benchmark tasks.
Graph Bayesian Optimization: Algorithms, Evaluations and Applications
Nov 06, 2018



Abstract:Network structure optimization is a fundamental task in complex network analysis. However, almost all the research on Bayesian optimization is aimed at optimizing the objective functions with vectorial inputs. In this work, we first present a flexible framework, denoted graph Bayesian optimization, to handle arbitrary graphs in the Bayesian optimization community. By combining the proposed framework with graph kernels, it can take full advantage of implicit graph structural features to supplement explicit features guessed according to the experience, such as tags of nodes and any attributes of graphs. The proposed framework can identify which features are more important during the optimization process. We apply the framework to solve four problems including two evaluations and two applications to demonstrate its efficacy and potential applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge