Decentralised Active Perception in Continuous Action Spaces for the Coordinated Escort Problem

We consider the coordinated escort problem, where a decentralised team of supporting robots implicitly assist the mission of higher-value principal robots. The defining challenge is how to evaluate the effect of supporting robots' actions on the principal robots' mission. To capture this effect, we define two novel auxiliary reward functions for supporting robots called satisfaction improvement and satisfaction entropy, which computes the improvement in probability of mission success, or the uncertainty thereof. Given these reward functions, we coordinate the entire team of principal and supporting robots using decentralised cross entropy method (Dec-CEM), a new extension of CEM to multi-agent systems based on the product distribution approximation. In a simulated object avoidance scenario, our planning framework demonstrates up to two-fold improvement in task satisfaction against conventional decoupled information gathering.The significance of our results is to introduce a new family of algorithmic problems that will enable important new practical applications of heterogeneous multi-robot systems.

Topological Trajectory Prediction with Homotopy Classes

Trajectory prediction in a cluttered environment is key to many important robotics tasks such as autonomous navigation. However, there are an infinite number of possible trajectories to consider. To simplify the space of trajectories under consideration, we utilise homotopy classes to partition the space into countably many mathematically equivalent classes. All members within a class demonstrate identical high-level motion with respect to the environment, i.e., travelling above or below an obstacle. This allows high-level prediction of a trajectory in terms of a sparse label identifying its homotopy class. We therefore present a light-weight learning framework based on variable-order Markov processes to learn and predict homotopy classes and thus high-level agent motion. By informing a Gaussian Mixture Model (GMM) with our homotopy class predictions, we see great improvements in low-level trajectory prediction compared to a naive GMM on a real dataset.

Motion planning in task space with Gromov-Hausdorff approximations

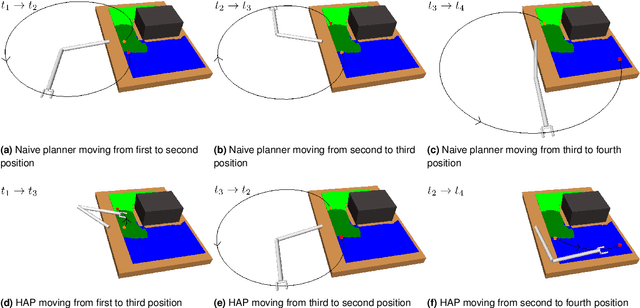
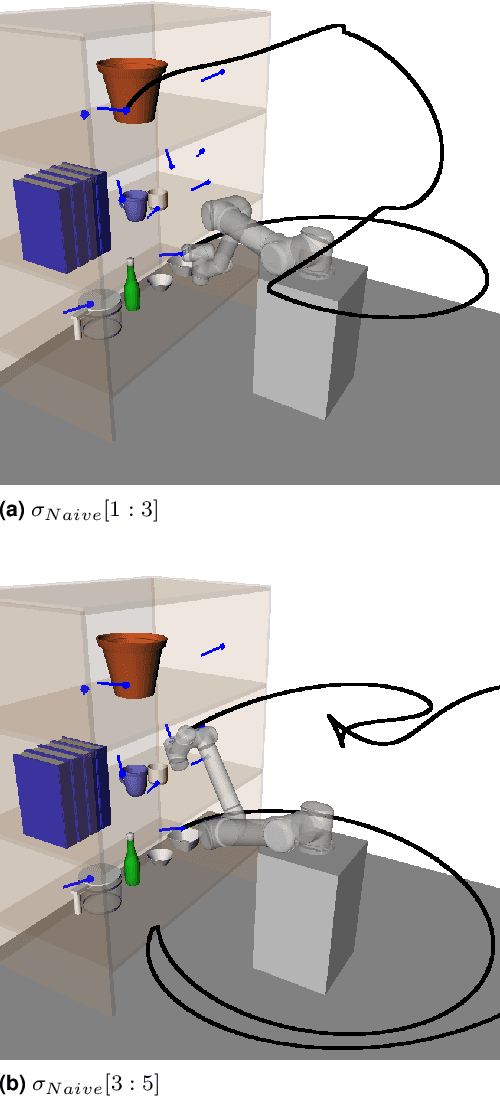
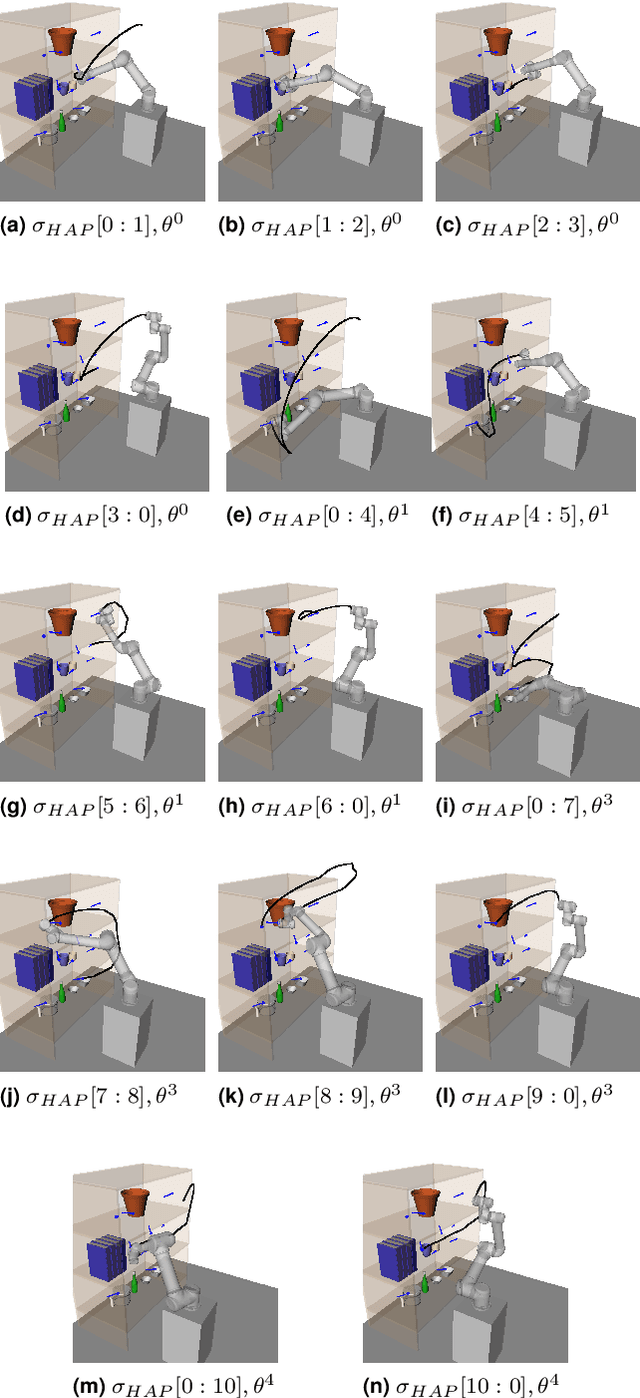
Applications of industrial robotic manipulators such as cobots can require efficient online motion planning in environments that have a combination of static and non-static obstacles. Existing general purpose planning methods often produce poor quality solutions when available computation time is restricted, or fail to produce a solution entirely. We propose a new motion planning framework designed to operate in a user-defined task space, as opposed to the robot's workspace, that intentionally trades off workspace generality for planning and execution time efficiency. Our framework automatically constructs trajectory libraries that are queried online, similar to previous methods that exploit offline computation. Importantly, our method also offers bounded suboptimality guarantees on trajectory length. The key idea is to establish approximate isometries known as $\epsilon$-Gromov-Hausdorff approximations such that points that are close by in task space are also close in configuration space. These bounding relations further imply that trajectories can be smoothly concatenated, which enables our framework to address batch-query scenarios where the objective is to find a minimum length sequence of trajectories that visit an unordered set of goals. We evaluate our framework in simulation with several kinematic configurations, including a manipulator mounted to a mobile base. Results demonstrate that our method achieves feasible real-time performance for practical applications and suggest interesting opportunities for extending its capabilities.

Informative Planning for Worst-Case Error Minimisation in Sparse Gaussian Process Regression

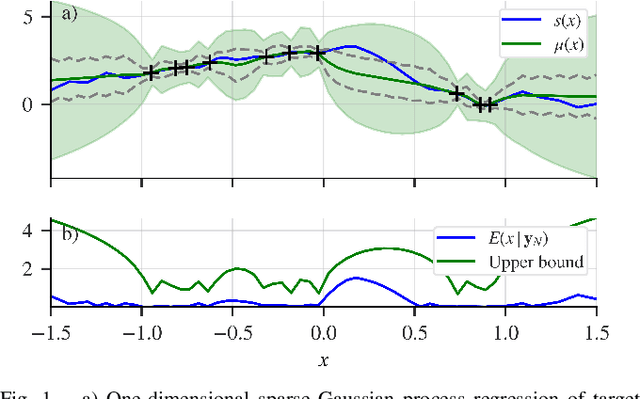
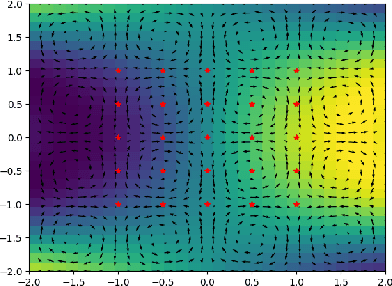
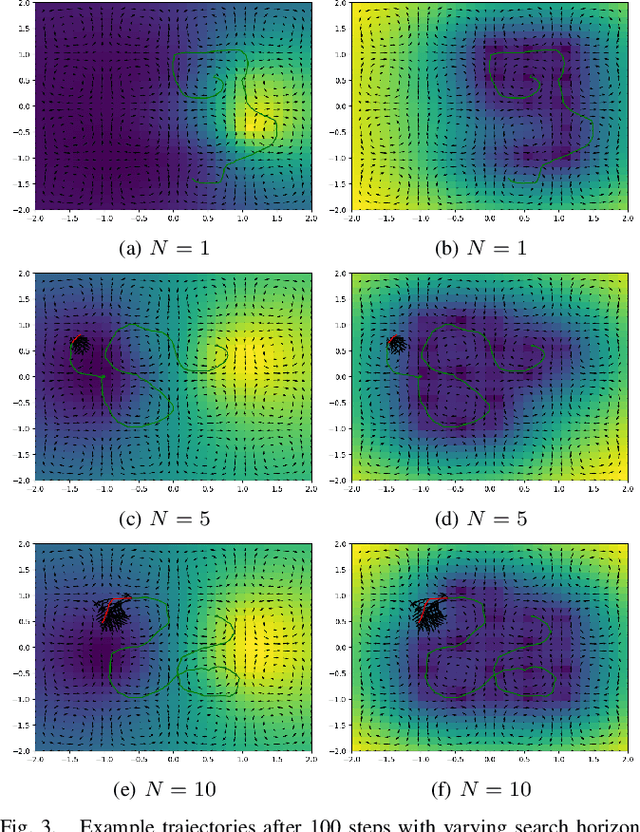
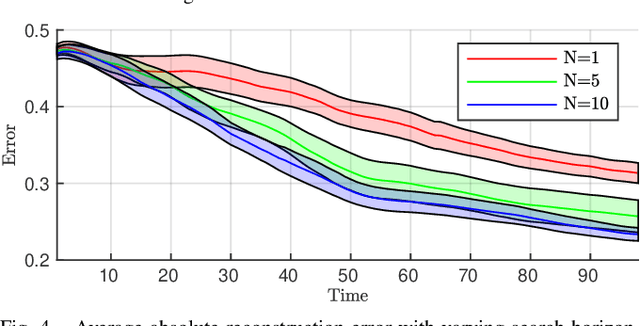
We present a planning framework for minimising the deterministic worst-case error in sparse Gaussian process (GP) regression. We first derive a universal worst-case error bound for sparse GP regression with bounded noise using interpolation theory on reproducing kernel Hilbert spaces (RKHSs). By exploiting the conditional independence (CI) assumption central to sparse GP regression, we show that the worst-case error minimisation can be achieved by solving a posterior entropy minimisation problem. In turn, the posterior entropy minimisation problem is solved using a Gaussian belief space planning algorithm. We corroborate the proposed worst-case error bound in a simple 1D example, and test the planning framework in simulation for a 2D vehicle in a complex flow field. Our results demonstrate that the proposed posterior entropy minimisation approach is effective in minimising deterministic error, and outperforms the conventional measurement entropy maximisation formulation when the inducing points are fixed.

Active Information Acquisition under Arbitrary Unknown Disturbances

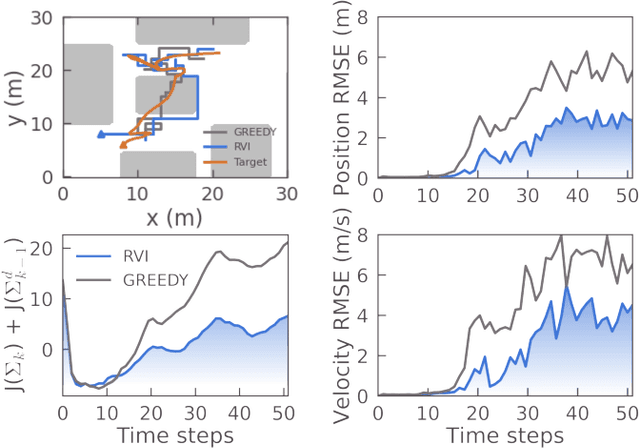
Trajectory optimization of sensing robots to actively gather information of targets has received much attention in the past. It is well-known that under the assumption of linear Gaussian target dynamics and sensor models the stochastic Active Information Acquisition problem is equivalent to a deterministic optimal control problem. However, the above-mentioned assumptions regarding the target dynamic model are limiting. In real-world scenarios, the target may be subject to disturbances whose models or statistical properties are hard or impossible to obtain. Typical scenarios include abrupt maneuvers, jumping disturbances due to interactions with the environment, anomalous misbehaviors due to system faults/attacks, etc. Motivated by the above considerations, in this paper we consider targets whose dynamic models are subject to arbitrary unknown inputs whose models or statistical properties are not assumed to be available. In particular, with the aid of an unknown input decoupled filter, we formulate the sensor trajectory planning problem to track evolution of the target state and analyse the resulting performance for both the state and unknown input evolution tracking. Inspired by concepts of Reduced Value Iteration, a suboptimal solution that expands a search tree via Forward Value Iteration with informativeness-based pruning is proposed. Concrete suboptimality performance guarantees for tracking both the state and the unknown input are established. Numerical simulations of a target tracking example are presented to compare the proposed solution with a greedy policy.