Real-time CARFAC Cochlea Model Acceleration on FPGA for Underwater Acoustic Sensing Systems

This paper presents a real-time, energy-efficient embedded system implementing an array of Cascade of Asymmetric Resonators with Fast-Acting Compression (CARFAC) cochlea models for underwater sound analysis. Built on the AMD Kria KV260 System-on-Module (SoM), the system integrates a Rust-based software framework on the processor for real-time interfacing and synchronization with multiple hydrophone inputs, and a hardware-accelerated implementation of the CARFAC models on a Field-Programmable Gate Array (FPGA) for real-time sound pre-processing. Compared to prior work, the CARFAC accelerator achieves improved scalability and processing speed while reducing resource usage through optimized time-multiplexing, pipelined design, and elimination of costly division circuits. Experimental results demonstrate 13.5% hardware utilization for a single 64-channel CARFAC instance and a whole board power consumption of 3.11 W when processing a 256 kHz input signal in real time.

Decentralised Active Perception in Continuous Action Spaces for the Coordinated Escort Problem

We consider the coordinated escort problem, where a decentralised team of supporting robots implicitly assist the mission of higher-value principal robots. The defining challenge is how to evaluate the effect of supporting robots' actions on the principal robots' mission. To capture this effect, we define two novel auxiliary reward functions for supporting robots called satisfaction improvement and satisfaction entropy, which computes the improvement in probability of mission success, or the uncertainty thereof. Given these reward functions, we coordinate the entire team of principal and supporting robots using decentralised cross entropy method (Dec-CEM), a new extension of CEM to multi-agent systems based on the product distribution approximation. In a simulated object avoidance scenario, our planning framework demonstrates up to two-fold improvement in task satisfaction against conventional decoupled information gathering.The significance of our results is to introduce a new family of algorithmic problems that will enable important new practical applications of heterogeneous multi-robot systems.

3D Ensemble-Based Online Oceanic Flow Field Estimation for Underwater Glider Path Planning

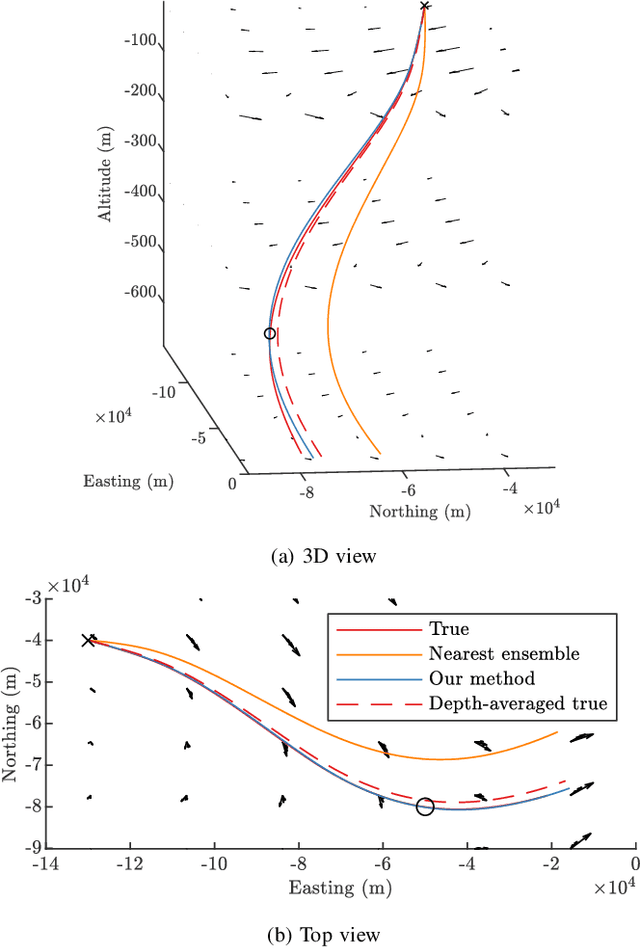
Estimating ocean flow fields in 3D is a critical step in enabling the reliable operation of underwater gliders and other small, low-powered autonomous marine vehicles. Existing methods produce depth-averaged 2D layers arranged at discrete vertical intervals, but this type of estimation can lead to severe navigation errors. Based on the observation that real-world ocean currents exhibit relatively low velocity vertical components, we propose an accurate 3D estimator that extends our previous work in estimating 2D flow fields as a linear combination of basis flows. The proposed algorithm uses data from ensemble forecasting to build a set of 3D basis flows, and then iteratively updates basis coefficients using point measurements of underwater currents. We report results from experiments using actual ensemble forecasts and synthetic measurements to compare the performance of our method to the direct 3D extension of the previous work. These results show that our method produces estimates with dramatically lower error metrics, with and without measurement noise.

Estimation of Spatially-Correlated Ocean Currents from Ensemble Forecasts and Online Measurements

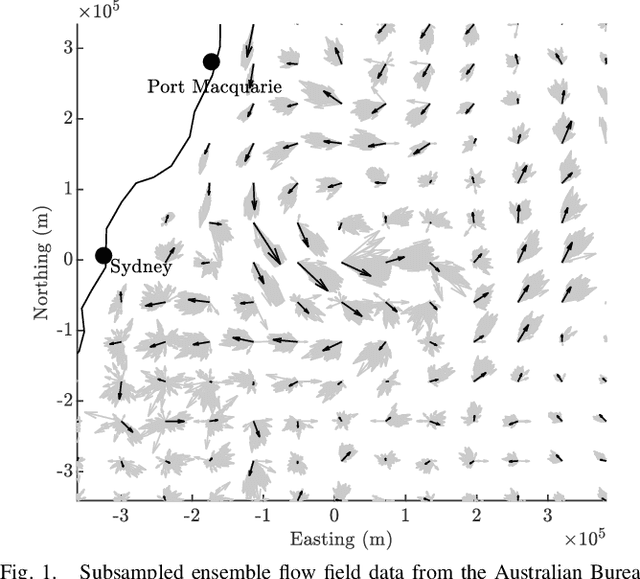
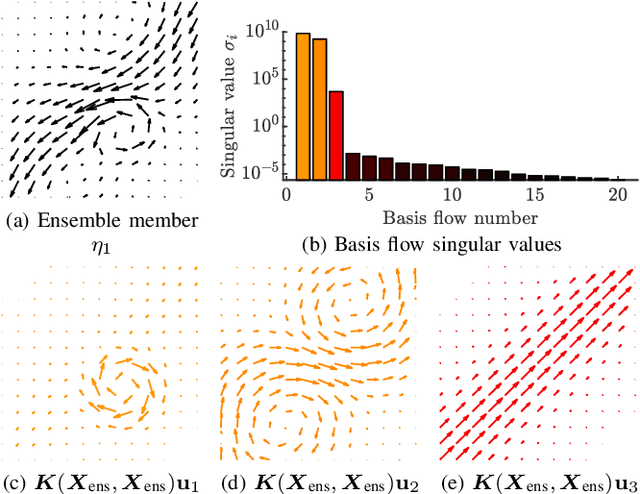
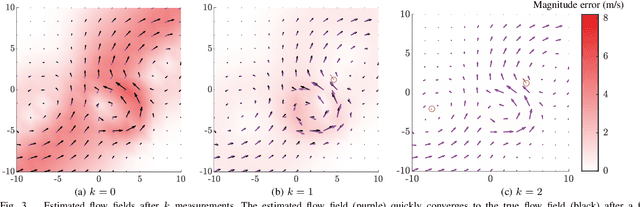
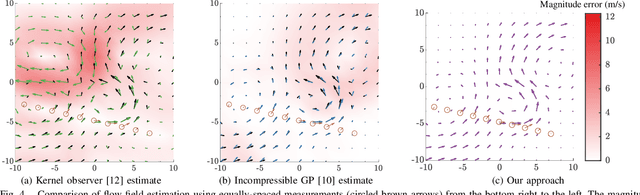
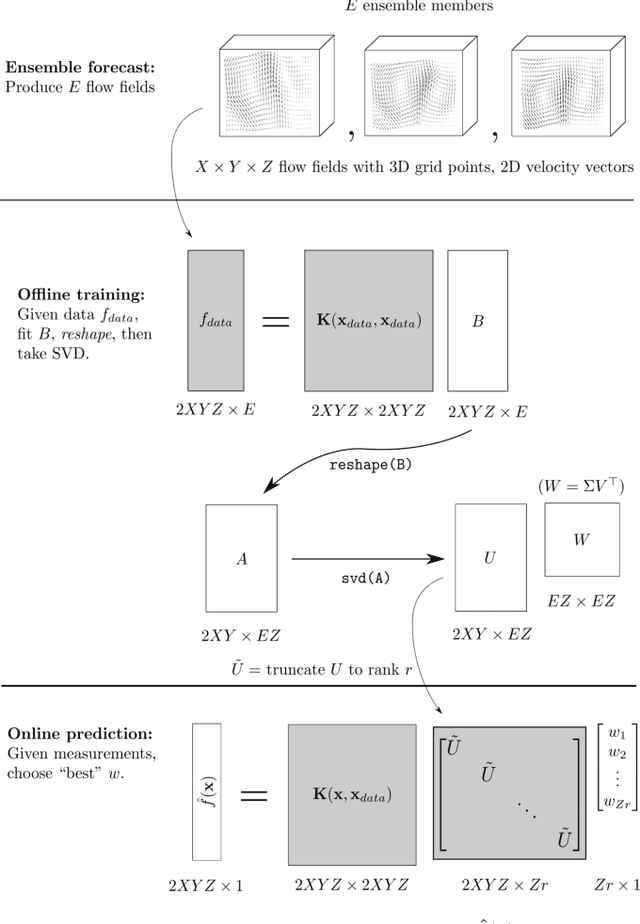
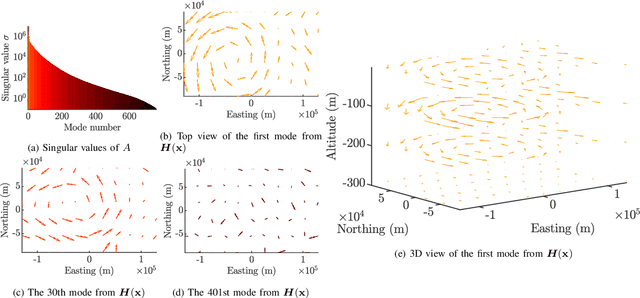
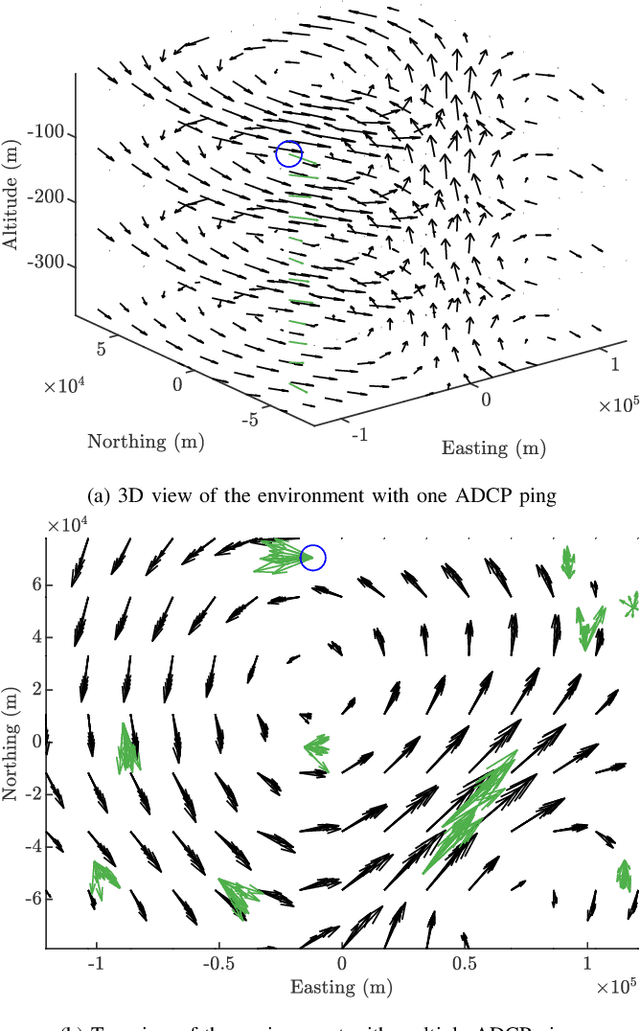
We present a method to estimate two-dimensional, time-invariant oceanic flow fields based on data from both ensemble forecasts and online measurements. Our method produces a realistic estimate in a computationally efficient manner suitable for use in marine robotics for path planning and related applications. We use kernel methods and singular value decomposition to find a compact model of the ensemble data that is represented as a linear combination of basis flow fields and that preserves the spatial correlations present in the data. Online measurements of ocean current, taken for example by marine robots, can then be incorporated using recursive Bayesian estimation. We provide computational analysis, performance comparisons with related methods, and demonstration with real-world ensemble data to show the computational efficiency and validity of our method. Possible applications in addition to path planning include active perception for model improvement through deliberate choice of measurement locations.

Distance and Steering Heuristics for Streamline-Based Flow Field Planning

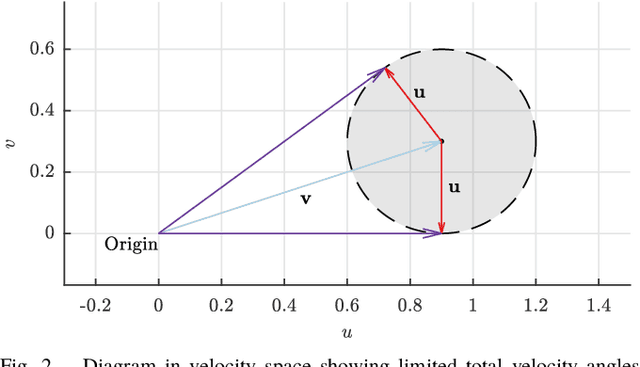
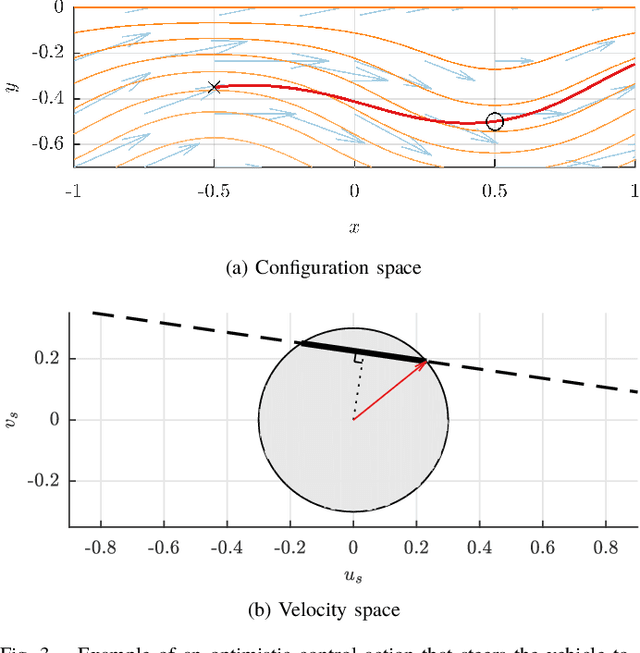
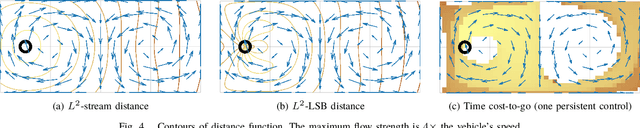
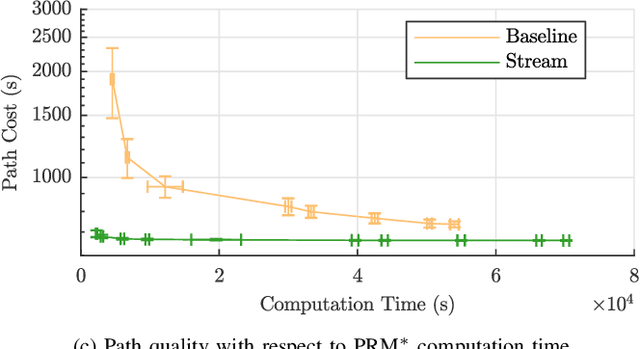
Motion planning for vehicles under the influence of flow fields can benefit from the idea of streamline-based planning, which exploits ideas from fluid dynamics to achieve computational efficiency. Important to such planners is an efficient means of computing the travel distance and direction between two points in free space, but this is difficult to achieve in strong incompressible flows such as ocean currents. We propose two useful distance functions in analytical form that combine Euclidean distance with values of the stream function associated with a flow field, and with an estimation of the strength of the opposing flow between two points. Further, we propose steering heuristics that are useful for steering towards a sampled point. We evaluate these ideas by integrating them with RRT* and comparing the algorithm's performance with state-of-the-art methods in an artificial flow field and in actual ocean prediction data in the region of the dominant East Australian Current between Sydney and Brisbane. Results demonstrate the method's computational efficiency and ability to find high-quality paths outperforming state-of-the-art methods, and show promise for practical use with autonomous marine robots.

Streamline-Based Control of Underwater Gliders in 3D Environments

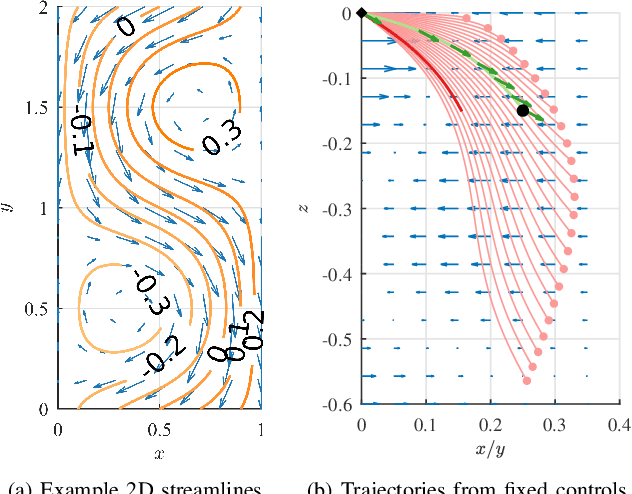
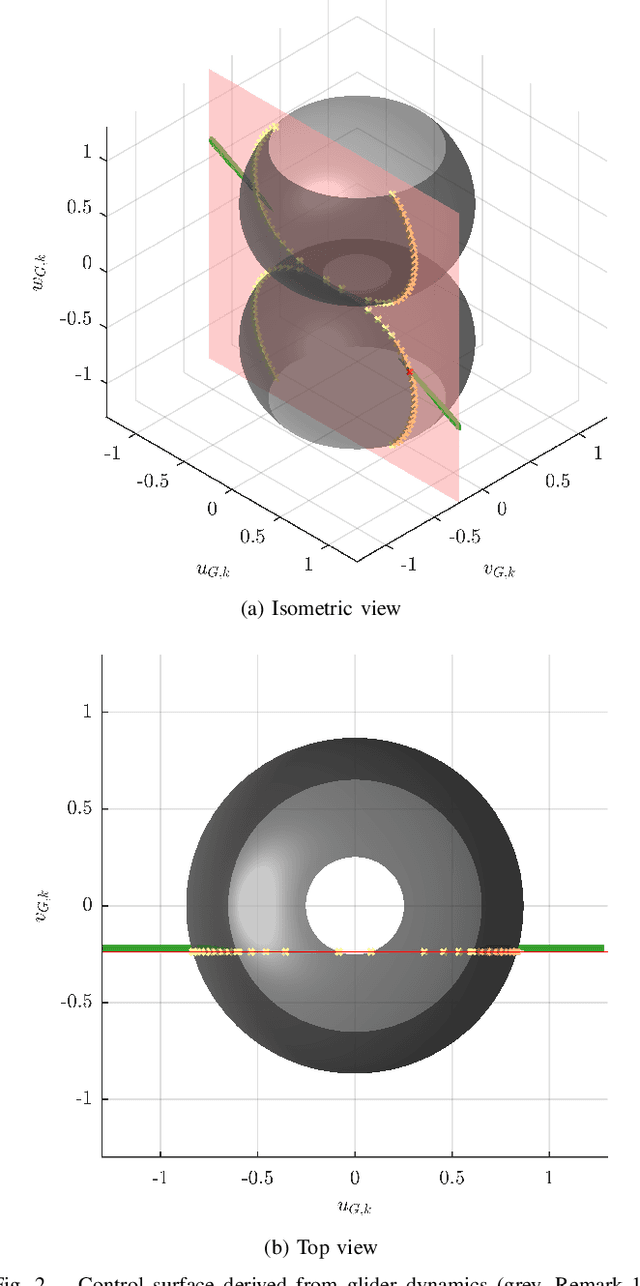
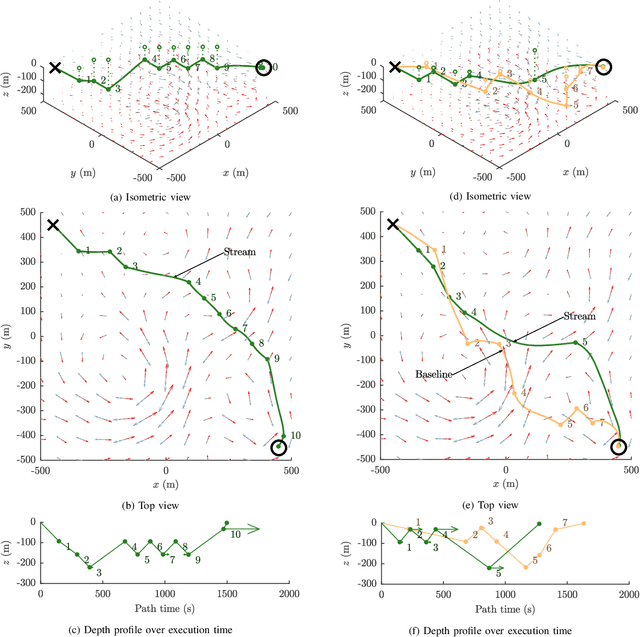
Autonomous underwater gliders use buoyancy control to achieve forward propulsion via a sawtooth-like, rise-and-fall trajectory. Because gliders are slow-moving relative to ocean currents, glider control must consider the effect of oceanic flows. In previous work, we proposed a method to control underwater vehicles in the (horizontal) plane by describing such oceanic flows in terms of streamlines, which are the level sets of stream functions. However, the general analytical form of streamlines in 3D is unknown. In this paper, we show how streamline control can be used in 3D environments by assuming a 2.5D model of ocean currents. We provide an efficient algorithm that acts as a steering function for a single rise or dive component of the glider's sawtooth trajectory, integrate this algorithm within a sampling-based motion planning framework to support long-distance path planning, and provide several examples in simulation in comparison with a baseline method. The key to our method's computational efficiency is an elegant dimensionality reduction to a 1D control region. Streamline-based control can be integrated within various sampling-based frameworks and allows for online planning for gliders in complicated oceanic flows.

Efficient Optimal Planning in non-FIFO Time-Dependent Flow Fields

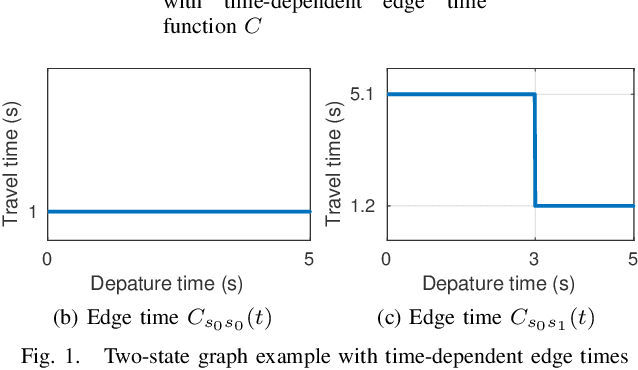
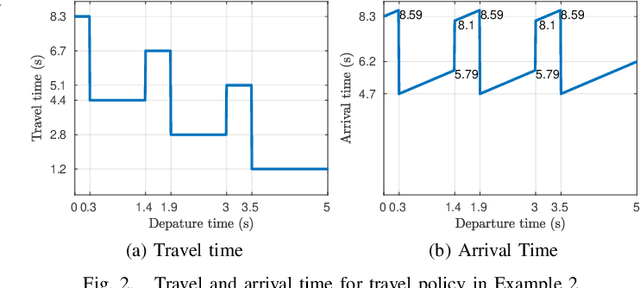
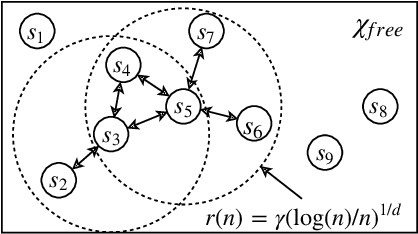
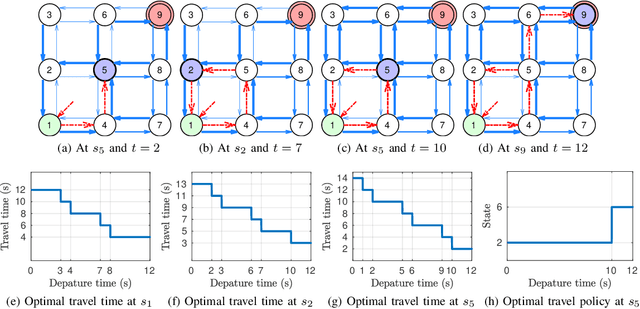
We propose an algorithm for solving the time-dependent shortest path problem in flow fields where the FIFO (first-in-first-out) assumption is violated. This problem variant is important for autonomous vehicles in the ocean, for example, that cannot arbitrarily hover in a fixed position and that are strongly influenced by time-varying ocean currents. Although polynomial-time solutions are available for discrete-time problems, the continuous-time non-FIFO case is NP-hard with no known relevant special cases. Our main result is to show that this problem can be solved in polynomial time if the edge travel time functions are piecewise-constant, agreeing with existing worst-case bounds for FIFO problems with restricted slopes. We present a minimum-time algorithm for graphs that allows for paths with finite-length cycles, and then embed this algorithm within an asymptotically optimal sampling-based framework to find time-optimal paths in flows. The algorithm relies on an efficient data structure to represent and manipulate piecewise-constant functions and is straightforward to implement. We illustrate the behaviour of the algorithm in an example based on a common ocean vortex model in addition to simpler graph-based examples.

Online Estimation of Ocean Current from Sparse GPS Data for Underwater Vehicles

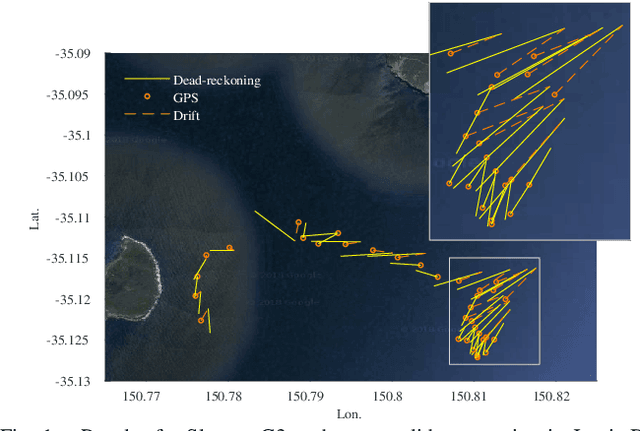
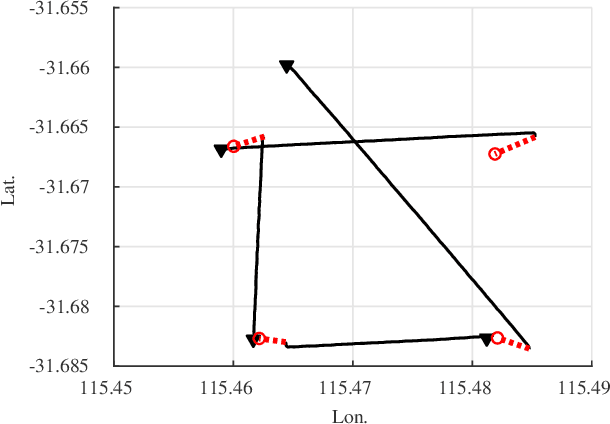
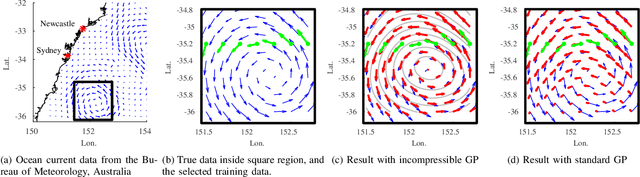
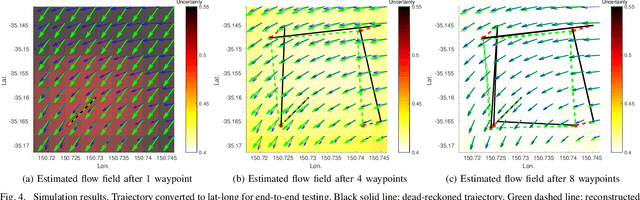
Underwater robots are subject to position drift due to the effect of ocean currents and the lack of accurate localisation while submerged. We are interested in exploiting such position drift to estimate the ocean current in the surrounding area, thereby assisting navigation and planning. We present a Gaussian process~(GP)-based expectation-maximisation~(EM) algorithm that estimates the underlying ocean current using sparse GPS data obtained on the surface and dead-reckoned position estimates. We first develop a specialised GP regression scheme that exploits the incompressibility of ocean currents to counteract the underdetermined nature of the problem. We then use the proposed regression scheme in an EM algorithm that estimates the best-fitting ocean current in between each GPS fix. The proposed algorithm is validated in simulation and on a real dataset, and is shown to be capable of reconstructing the underlying ocean current field. We expect to use this algorithm to close the loop between planning and estimation for underwater navigation in unknown ocean currents.

Streamlines for Motion Planning in Underwater Currents

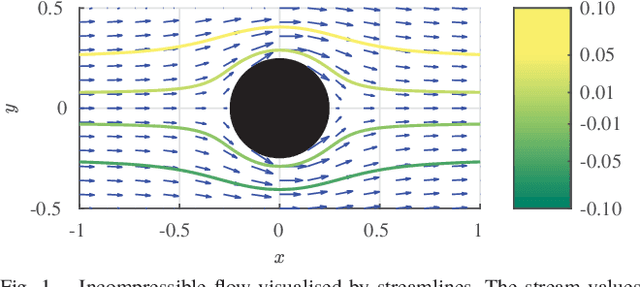
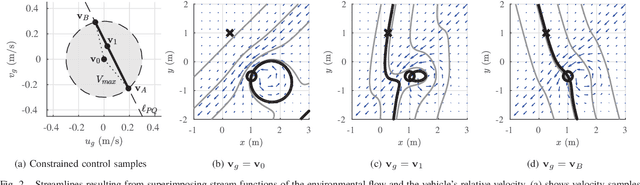
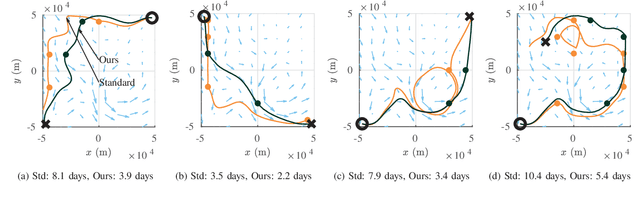
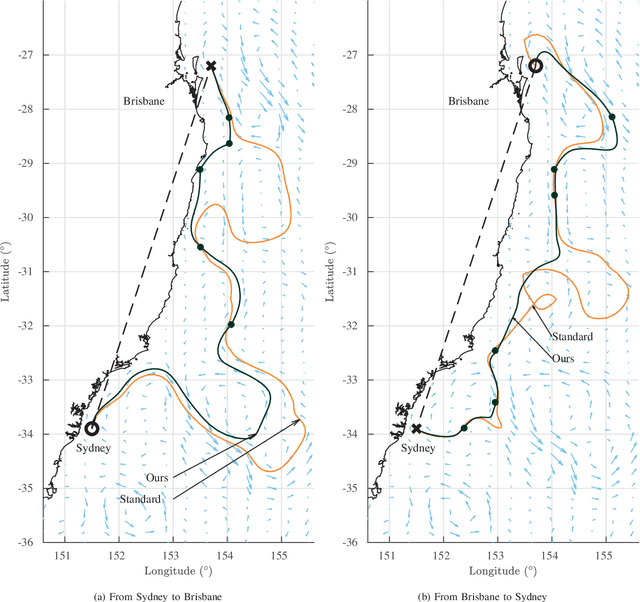
Motion planning for underwater vehicles must consider the effect of ocean currents. We present an efficient method to compute reachability and cost between sample points in sampling-based motion planning that supports long-range planning over hundreds of kilometres in complicated flows. The idea is to search a reduced space of control inputs that consists of stream functions whose level sets, or streamlines, optimally connect two given points. Such stream functions are generated by superimposing a control input onto the underlying current flow. A streamline represents the resulting path that a vehicle would follow as it is carried along by the current given that control input. We provide rigorous analysis that shows how our method avoids exhaustive search of the control space, and demonstrate simulated examples in complicated flows including a traversal along the east coast of Australia, using actual current predictions, between Sydney and Brisbane.