Decentralised Intelligence, Surveillance, and Reconnaissance in Unknown Environments with Heterogeneous Multi-Robot Systems

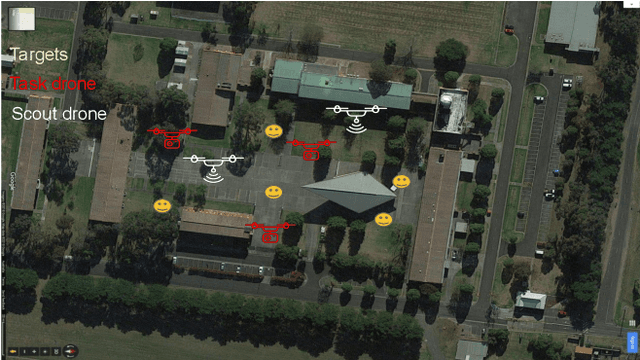
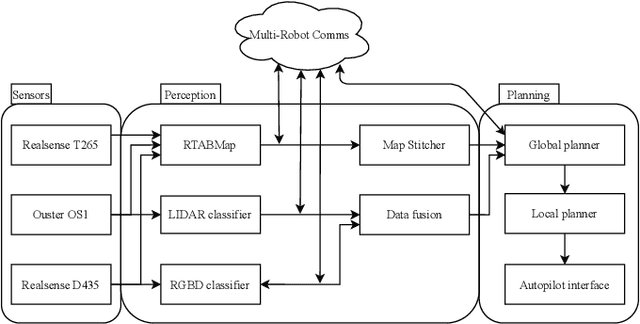
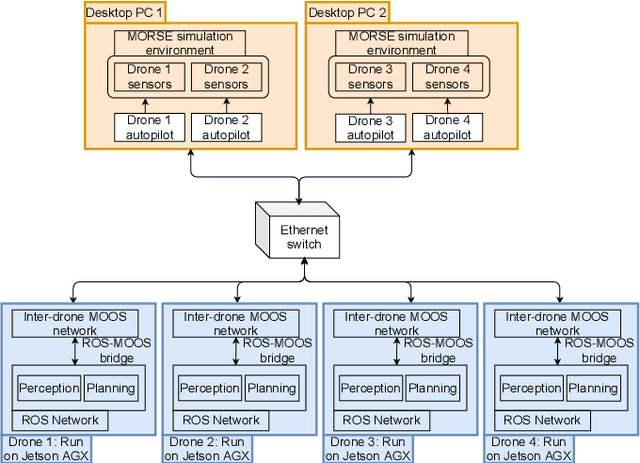
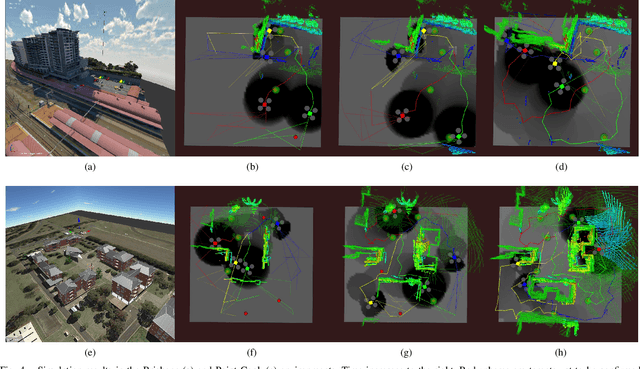
We present the design and implementation of a decentralised, heterogeneous multi-robot system for performing intelligence, surveillance and reconnaissance (ISR) in an unknown environment. The team consists of functionally specialised robots that gather information and others that perform a mission-specific task, and is coordinated to achieve simultaneous exploration and exploitation in the unknown environment. We present a practical implementation of such a system, including decentralised inter-robot localisation, mapping, data fusion and coordination. The system is demonstrated in an efficient distributed simulation. We also describe an UAS platform for hardware experiments, and the ongoing progress.

An Upper Confidence Bound for Simultaneous Exploration and Exploitation in Heterogeneous Multi-Robot Systems

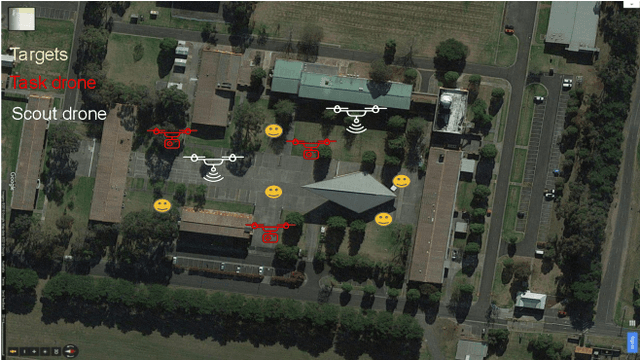
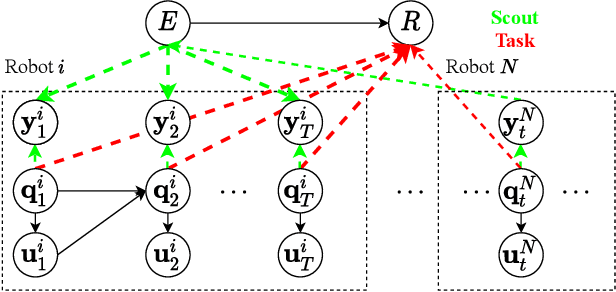
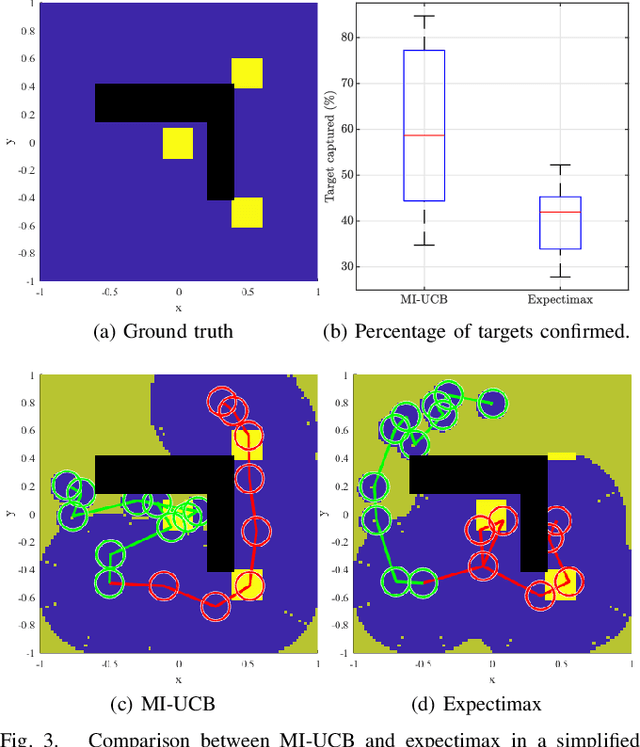
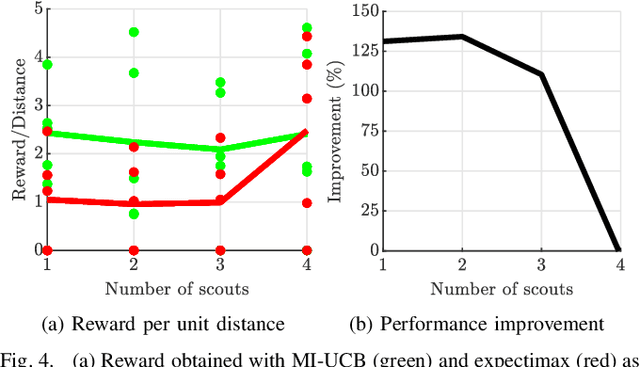
Heterogeneous multi-robot systems are advantageous for operations in unknown environments because functionally specialised robots can gather environmental information, while others perform tasks. We define this decomposition as the scout-task robot architecture and show how it avoids the need to explicitly balance exploration and exploitation~by permitting the system to do both simultaneously. The challenge is to guide exploration in a way that improves overall performance for time-limited tasks. We derive a novel upper confidence bound for simultaneous exploration and exploitation based on mutual information and present a general solution for scout-task coordination using decentralised Monte Carlo tree search. We evaluate the performance of our algorithms in a multi-drone surveillance scenario in which scout robots are equipped with low-resolution, long-range sensors and task robots capture detailed information using short-range sensors. The results address a new class of coordination problem for heterogeneous teams that has many practical applications.

3D Ensemble-Based Online Oceanic Flow Field Estimation for Underwater Glider Path Planning

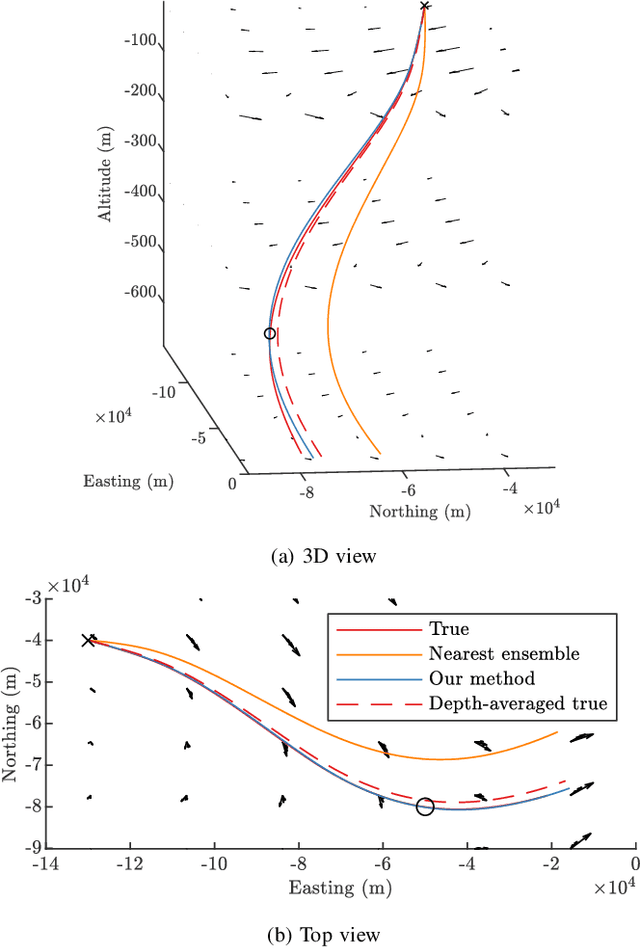
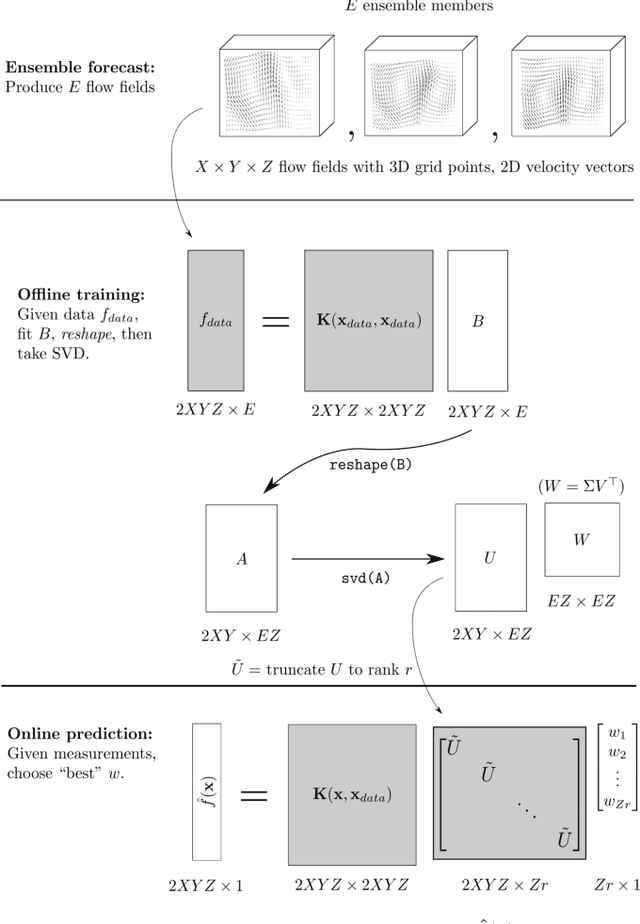
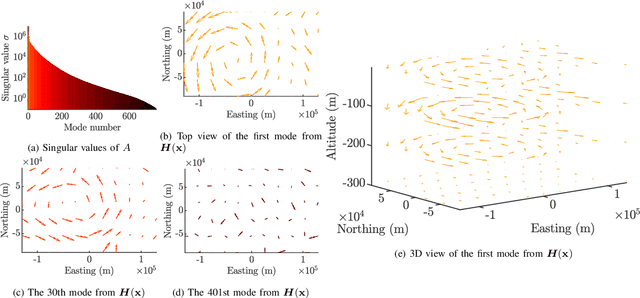
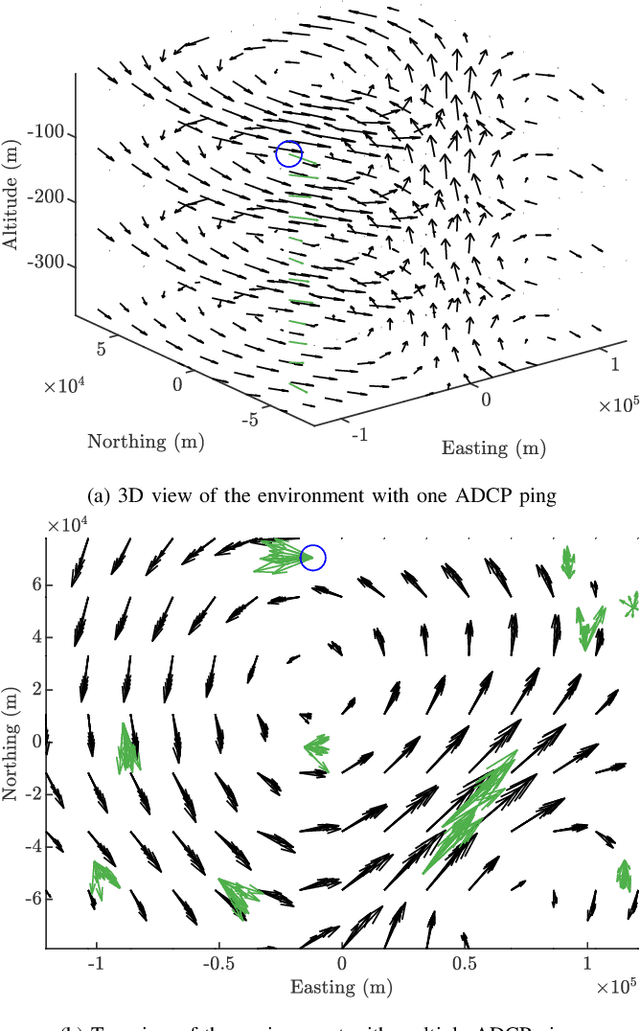
Estimating ocean flow fields in 3D is a critical step in enabling the reliable operation of underwater gliders and other small, low-powered autonomous marine vehicles. Existing methods produce depth-averaged 2D layers arranged at discrete vertical intervals, but this type of estimation can lead to severe navigation errors. Based on the observation that real-world ocean currents exhibit relatively low velocity vertical components, we propose an accurate 3D estimator that extends our previous work in estimating 2D flow fields as a linear combination of basis flows. The proposed algorithm uses data from ensemble forecasting to build a set of 3D basis flows, and then iteratively updates basis coefficients using point measurements of underwater currents. We report results from experiments using actual ensemble forecasts and synthetic measurements to compare the performance of our method to the direct 3D extension of the previous work. These results show that our method produces estimates with dramatically lower error metrics, with and without measurement noise.

Estimation of Spatially-Correlated Ocean Currents from Ensemble Forecasts and Online Measurements

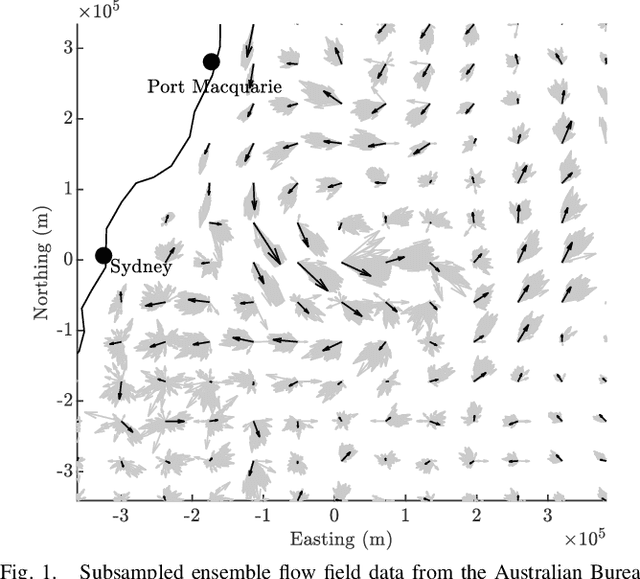
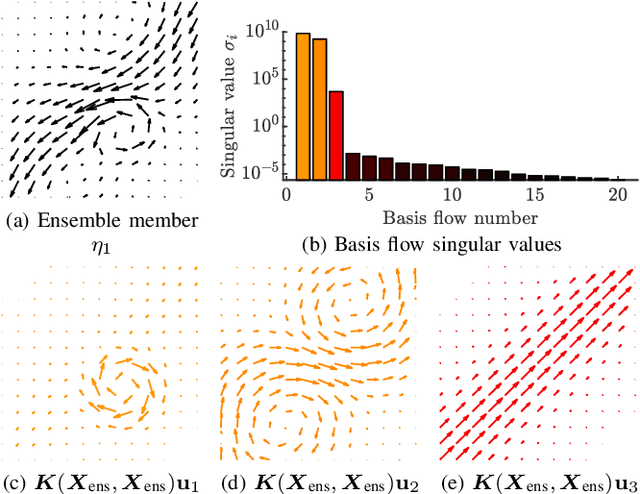
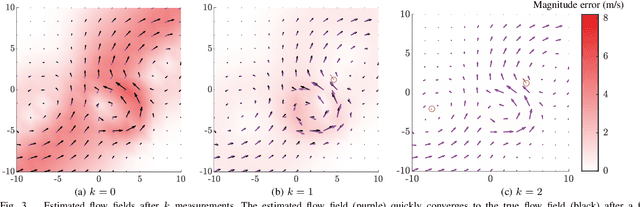
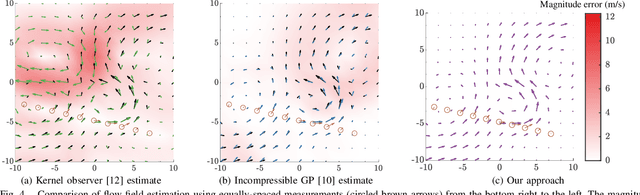
We present a method to estimate two-dimensional, time-invariant oceanic flow fields based on data from both ensemble forecasts and online measurements. Our method produces a realistic estimate in a computationally efficient manner suitable for use in marine robotics for path planning and related applications. We use kernel methods and singular value decomposition to find a compact model of the ensemble data that is represented as a linear combination of basis flow fields and that preserves the spatial correlations present in the data. Online measurements of ocean current, taken for example by marine robots, can then be incorporated using recursive Bayesian estimation. We provide computational analysis, performance comparisons with related methods, and demonstration with real-world ensemble data to show the computational efficiency and validity of our method. Possible applications in addition to path planning include active perception for model improvement through deliberate choice of measurement locations.

Analysis of minima for geodesic and chordal cost for a minimal 2D pose-graph SLAM problem

In this paper, we show that for a minimal pose-graph problem, even in the ideal case of perfect measurements and spherical covariance, using the so-called "wrap function" when comparing angles results in multiple suboptimal local minima. We numerically estimate regions of attraction to these local minima for some numerical examples, and give evidence to show that they are of nonzero measure. In contrast, under the same assumptions, we show that the \textit{chordal distance} representation of angle error has a unique minimum up to periodicity. For chordal cost, we also search for initial conditions that fail to converge to the global minimum, and find that this occurs with far fewer points than with geodesic cost.