Field trial on Ocean Estimation for Multi-Vessel Multi-Float-based Active perception

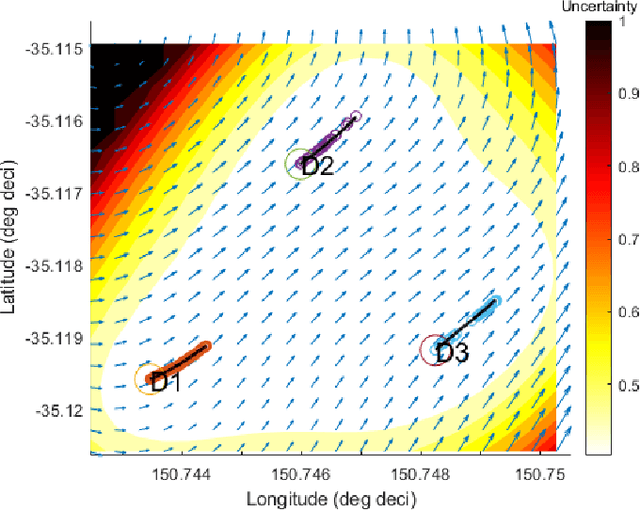
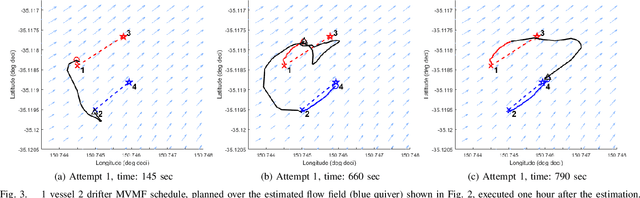
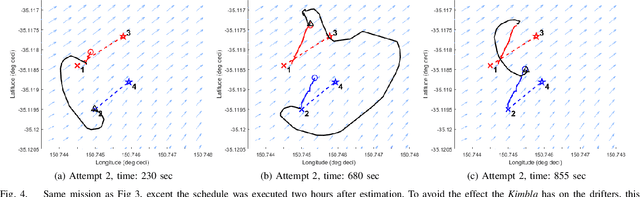
Marine vehicles have been used for various scientific missions where information over features of interest is collected. In order to maximise efficiency in collecting information over a large search space, we should be able to deploy a large number of autonomous vehicles that make a decision based on the latest understanding of the target feature in the environment. In our previous work, we have presented a hierarchical framework for the multi-vessel multi-float (MVMF) problem where surface vessels drop and pick up underactuated floats in a time-minimal way. In this paper, we present the field trial results using the framework with a number of drifters and floats. We discovered a number of important aspects that need to be considered in the proposed framework, and present the potential approaches to address the challenges.

Streamline-Based Control of Underwater Gliders in 3D Environments

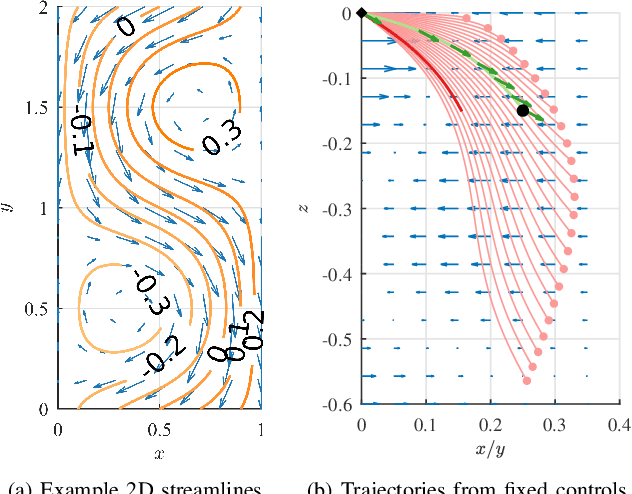
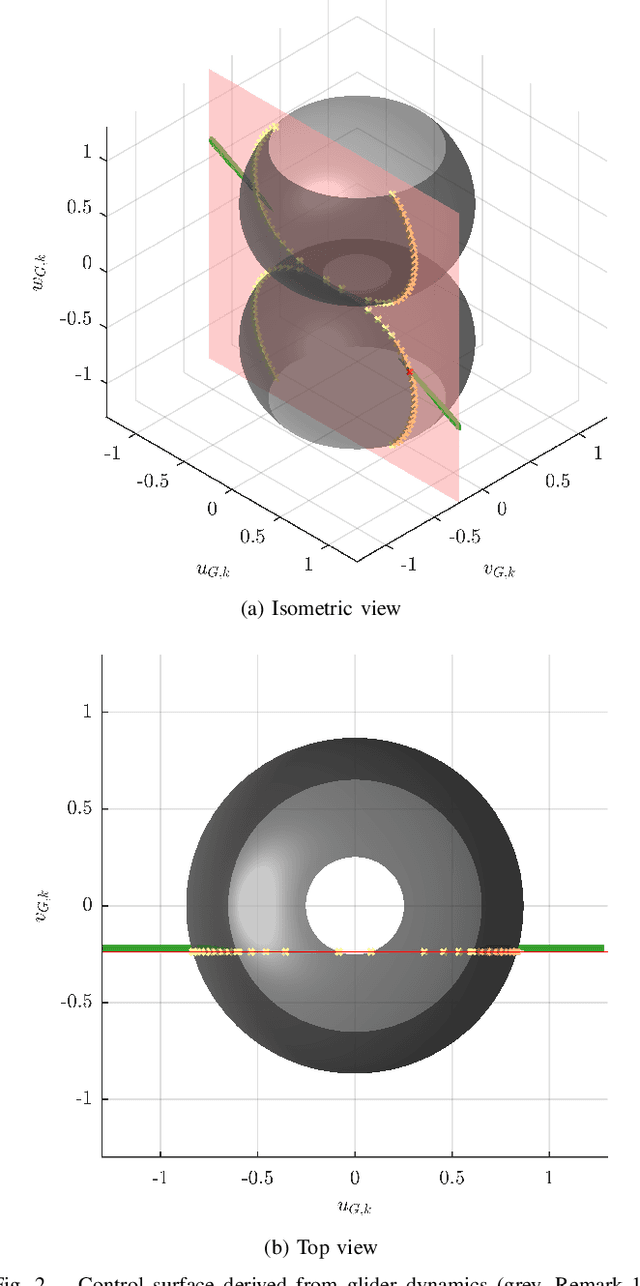
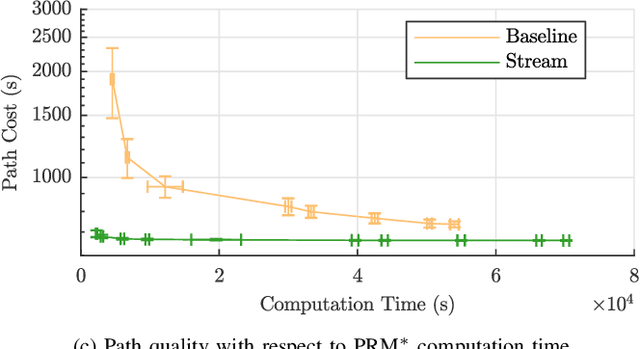
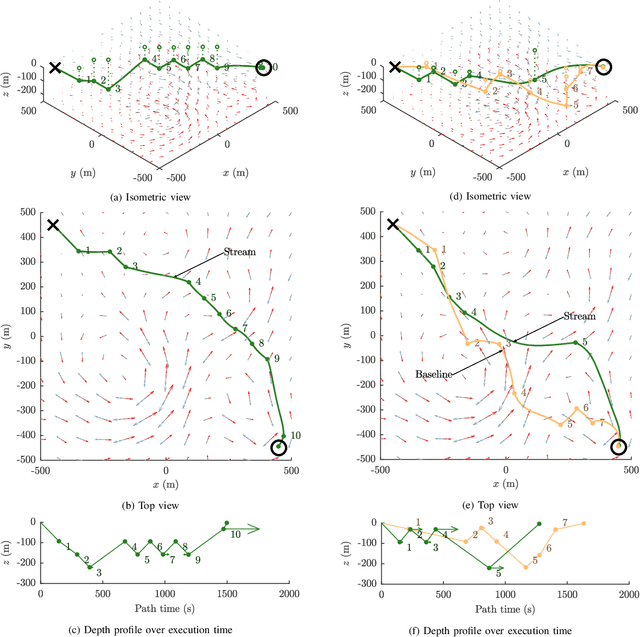
Autonomous underwater gliders use buoyancy control to achieve forward propulsion via a sawtooth-like, rise-and-fall trajectory. Because gliders are slow-moving relative to ocean currents, glider control must consider the effect of oceanic flows. In previous work, we proposed a method to control underwater vehicles in the (horizontal) plane by describing such oceanic flows in terms of streamlines, which are the level sets of stream functions. However, the general analytical form of streamlines in 3D is unknown. In this paper, we show how streamline control can be used in 3D environments by assuming a 2.5D model of ocean currents. We provide an efficient algorithm that acts as a steering function for a single rise or dive component of the glider's sawtooth trajectory, integrate this algorithm within a sampling-based motion planning framework to support long-distance path planning, and provide several examples in simulation in comparison with a baseline method. The key to our method's computational efficiency is an elegant dimensionality reduction to a 1D control region. Streamline-based control can be integrated within various sampling-based frameworks and allows for online planning for gliders in complicated oceanic flows.

Efficient Optimal Planning in non-FIFO Time-Dependent Flow Fields

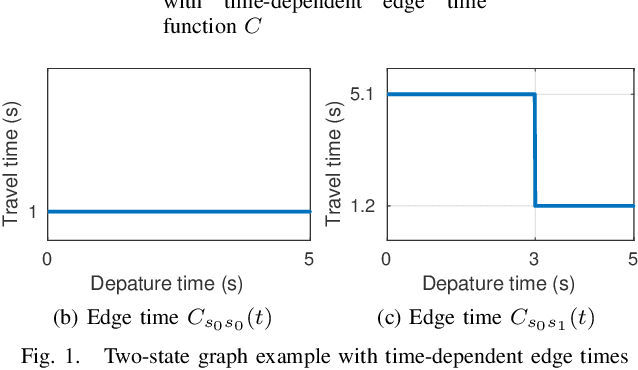
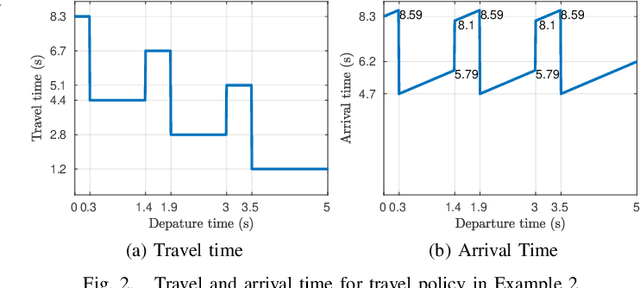
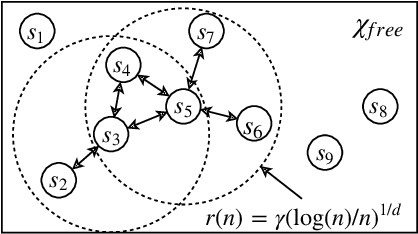
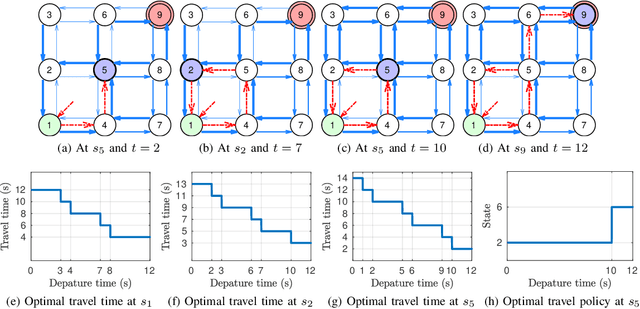
We propose an algorithm for solving the time-dependent shortest path problem in flow fields where the FIFO (first-in-first-out) assumption is violated. This problem variant is important for autonomous vehicles in the ocean, for example, that cannot arbitrarily hover in a fixed position and that are strongly influenced by time-varying ocean currents. Although polynomial-time solutions are available for discrete-time problems, the continuous-time non-FIFO case is NP-hard with no known relevant special cases. Our main result is to show that this problem can be solved in polynomial time if the edge travel time functions are piecewise-constant, agreeing with existing worst-case bounds for FIFO problems with restricted slopes. We present a minimum-time algorithm for graphs that allows for paths with finite-length cycles, and then embed this algorithm within an asymptotically optimal sampling-based framework to find time-optimal paths in flows. The algorithm relies on an efficient data structure to represent and manipulate piecewise-constant functions and is straightforward to implement. We illustrate the behaviour of the algorithm in an example based on a common ocean vortex model in addition to simpler graph-based examples.