James Rayfield
AssetOpsBench: Benchmarking AI Agents for Task Automation in Industrial Asset Operations and Maintenance
Jun 04, 2025Abstract:AI for Industrial Asset Lifecycle Management aims to automate complex operational workflows -- such as condition monitoring, maintenance planning, and intervention scheduling -- to reduce human workload and minimize system downtime. Traditional AI/ML approaches have primarily tackled these problems in isolation, solving narrow tasks within the broader operational pipeline. In contrast, the emergence of AI agents and large language models (LLMs) introduces a next-generation opportunity: enabling end-to-end automation across the entire asset lifecycle. This paper envisions a future where AI agents autonomously manage tasks that previously required distinct expertise and manual coordination. To this end, we introduce AssetOpsBench -- a unified framework and environment designed to guide the development, orchestration, and evaluation of domain-specific agents tailored for Industry 4.0 applications. We outline the key requirements for such holistic systems and provide actionable insights into building agents that integrate perception, reasoning, and control for real-world industrial operations. The software is available at https://github.com/IBM/AssetOpsBench.
Efficient Encrypted Inference on Ensembles of Decision Trees
Mar 05, 2021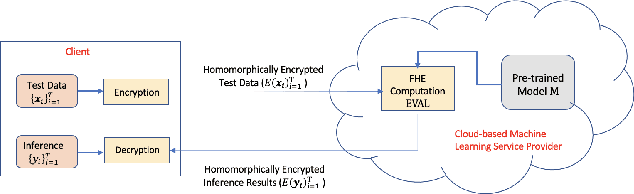

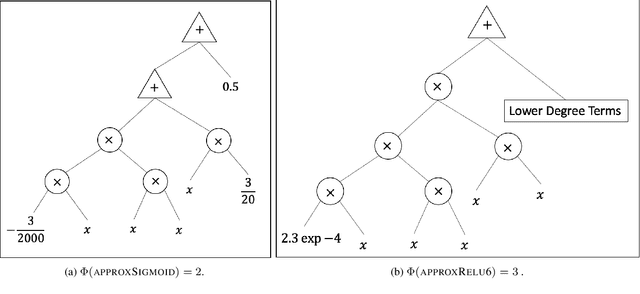
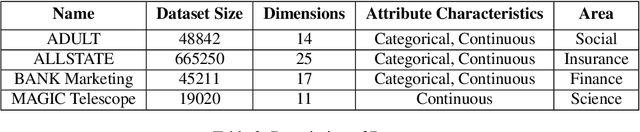
Abstract:Data privacy concerns often prevent the use of cloud-based machine learning services for sensitive personal data. While homomorphic encryption (HE) offers a potential solution by enabling computations on encrypted data, the challenge is to obtain accurate machine learning models that work within the multiplicative depth constraints of a leveled HE scheme. Existing approaches for encrypted inference either make ad-hoc simplifications to a pre-trained model (e.g., replace hard comparisons in a decision tree with soft comparators) at the cost of accuracy or directly train a new depth-constrained model using the original training set. In this work, we propose a framework to transfer knowledge extracted by complex decision tree ensembles to shallow neural networks (referred to as DTNets) that are highly conducive to encrypted inference. Our approach minimizes the accuracy loss by searching for the best DTNet architecture that operates within the given depth constraints and training this DTNet using only synthetic data sampled from the training data distribution. Extensive experiments on real-world datasets demonstrate that these characteristics are critical in ensuring that DTNet accuracy approaches that of the original tree ensemble. Our system is highly scalable and can perform efficient inference on batched encrypted (134 bits of security) data with amortized time in milliseconds. This is approximately three orders of magnitude faster than the standard approach of applying soft comparison at the internal nodes of the ensemble trees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge