Ultra-High-Resolution Detector Simulation with Intra-Event Aware GAN and Self-Supervised Relational Reasoning

Simulating high-resolution detector responses is a storage-costly and computationally intensive process that has long been challenging in particle physics. Despite the ability of deep generative models to make this process more cost-efficient, ultra-high-resolution detector simulation still proves to be difficult as it contains correlated and fine-grained mutual information within an event. To overcome these limitations, we propose Intra-Event Aware GAN (IEA-GAN), a novel fusion of Self-Supervised Learning and Generative Adversarial Networks. IEA-GAN presents a Relational Reasoning Module that approximates the concept of an ''event'' in detector simulation, allowing for the generation of correlated layer-dependent contextualized images for high-resolution detector responses with a proper relational inductive bias. IEA-GAN also introduces a new intra-event aware loss and a Uniformity loss, resulting in significant enhancements to image fidelity and diversity. We demonstrate IEA-GAN's application in generating sensor-dependent images for the high-granularity Pixel Vertex Detector (PXD), with more than 7.5M information channels and a non-trivial geometry, at the Belle II Experiment. Applications of this work include controllable simulation-based inference and event generation, high-granularity detector simulation such as at the HL-LHC (High Luminosity LHC), and fine-grained density estimation and sampling. To the best of our knowledge, IEA-GAN is the first algorithm for faithful ultra-high-resolution detector simulation with event-based reasoning.

Learning Tree Structures from Leaves For Particle Decay Reconstruction

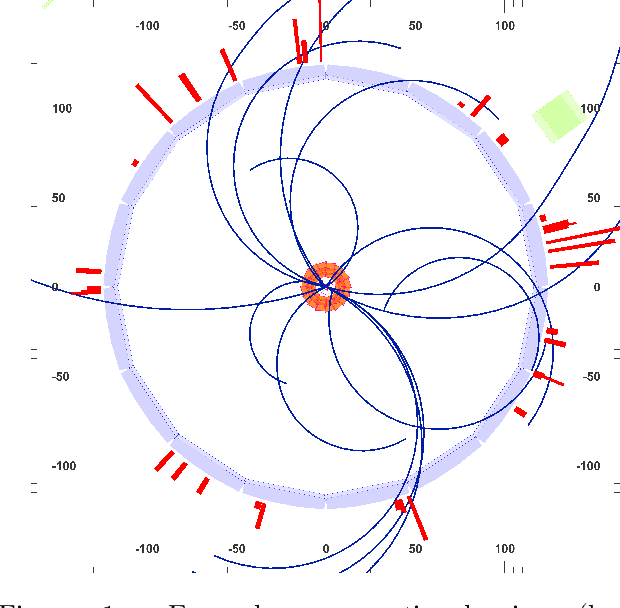
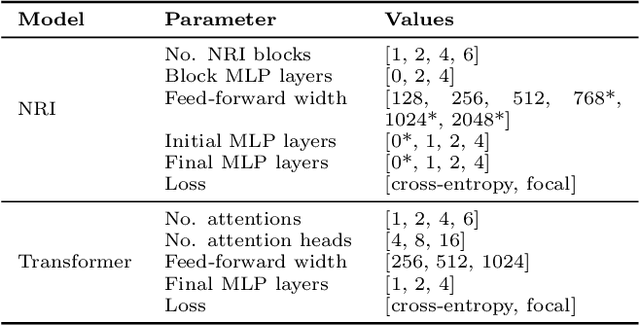
In this work, we present a neural approach to reconstructing rooted tree graphs describing hierarchical interactions, using a novel representation we term the Lowest Common Ancestor Generations (LCAG) matrix. This compact formulation is equivalent to the adjacency matrix, but enables learning a tree's structure from its leaves alone without the prior assumptions required if using the adjacency matrix directly. Employing the LCAG therefore enables the first end-to-end trainable solution which learns the hierarchical structure of varying tree sizes directly, using only the terminal tree leaves to do so. In the case of high-energy particle physics, a particle decay forms a hierarchical tree structure of which only the final products can be observed experimentally, and the large combinatorial space of possible trees makes an analytic solution intractable. We demonstrate the use of the LCAG as a target in the task of predicting simulated particle physics decay structures using both a Transformer encoder and a Neural Relational Inference encoder Graph Neural Network. With this approach, we are able to correctly predict the LCAG purely from leaf features for a maximum tree-depth of $8$ in $92.5\%$ of cases for trees up to $6$ leaves (including) and $59.7\%$ for trees up to $10$ in our simulated dataset.

Accelerated Computation of a High Dimensional Kolmogorov-Smirnov Distance

Statistical testing is widespread and critical for a variety of scientific disciplines. The advent of machine learning and the increase of computing power has increased the interest in the analysis and statistical testing of multidimensional data. We extend the powerful Kolmogorov-Smirnov two sample test to a high dimensional form in a similar manner to Fasano (Fasano, 1987). We call our result the d-dimensional Kolmogorov-Smirnov test (ddKS) and provide three novel contributions therewith: we develop an analytical equation for the significance of a given ddKS score, we provide an algorithm for computation of ddKS on modern computing hardware that is of constant time complexity for small sample sizes and dimensions, and we provide two approximate calculations of ddKS: one that reduces the time complexity to linear at larger sample sizes, and another that reduces the time complexity to linear with increasing dimension. We perform power analysis of ddKS and its approximations on a corpus of datasets and compare to other common high dimensional two sample tests and distances: Hotelling's T^2 test and Kullback-Leibler divergence. Our ddKS test performs well for all datasets, dimensions, and sizes tested, whereas the other tests and distances fail to reject the null hypothesis on at least one dataset. We therefore conclude that ddKS is a powerful multidimensional two sample test for general use, and can be calculated in a fast and efficient manner using our parallel or approximate methods. Open source implementations of all methods described in this work are located at https://github.com/pnnl/ddks.

Accelerating Neural Network Training with Distributed Asynchronous and Selective Optimization (DASO)

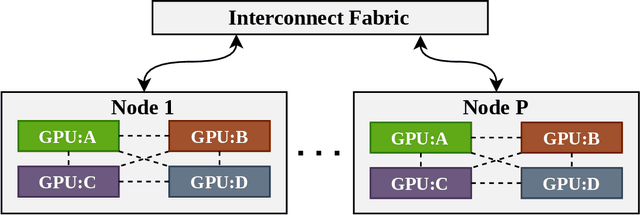
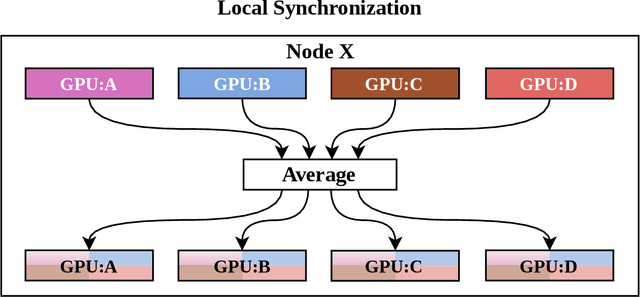
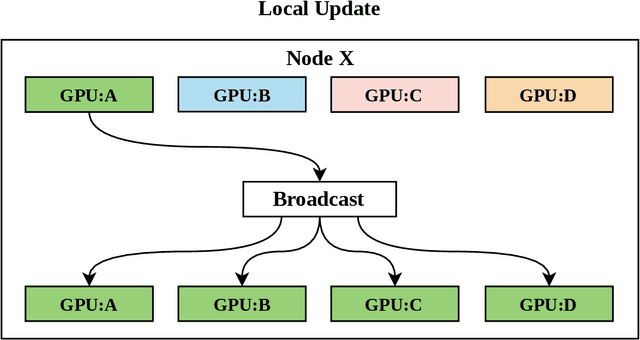
With increasing data and model complexities, the time required to train neural networks has become prohibitively large. To address the exponential rise in training time, users are turning to data parallel neural networks (DPNN) to utilize large-scale distributed resources on computer clusters. Current DPNN approaches implement the network parameter updates by synchronizing and averaging gradients across all processes with blocking communication operations. This synchronization is the central algorithmic bottleneck. To combat this, we introduce the Distributed Asynchronous and Selective Optimization (DASO) method which leverages multi-GPU compute node architectures to accelerate network training. DASO uses a hierarchical and asynchronous communication scheme comprised of node-local and global networks while adjusting the global synchronization rate during the learning process. We show that DASO yields a reduction in training time of up to 34% on classical and state-of-the-art networks, as compared to other existing data parallel training methods.