Ilias Tsaklidis
Learning Tree Structures from Leaves For Particle Decay Reconstruction
Sep 01, 2022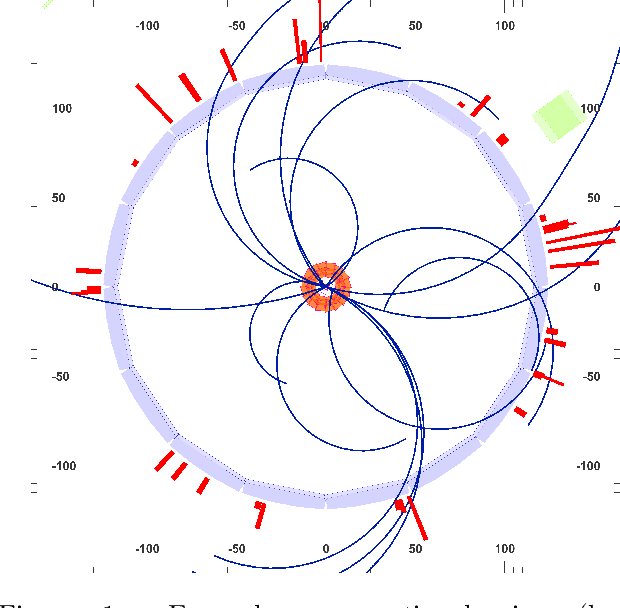
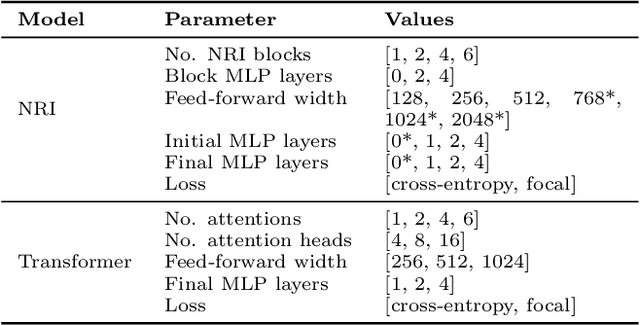
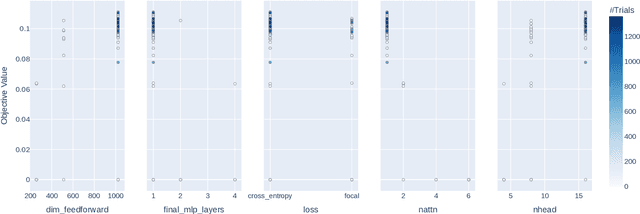

Abstract:In this work, we present a neural approach to reconstructing rooted tree graphs describing hierarchical interactions, using a novel representation we term the Lowest Common Ancestor Generations (LCAG) matrix. This compact formulation is equivalent to the adjacency matrix, but enables learning a tree's structure from its leaves alone without the prior assumptions required if using the adjacency matrix directly. Employing the LCAG therefore enables the first end-to-end trainable solution which learns the hierarchical structure of varying tree sizes directly, using only the terminal tree leaves to do so. In the case of high-energy particle physics, a particle decay forms a hierarchical tree structure of which only the final products can be observed experimentally, and the large combinatorial space of possible trees makes an analytic solution intractable. We demonstrate the use of the LCAG as a target in the task of predicting simulated particle physics decay structures using both a Transformer encoder and a Neural Relational Inference encoder Graph Neural Network. With this approach, we are able to correctly predict the LCAG purely from leaf features for a maximum tree-depth of $8$ in $92.5\%$ of cases for trees up to $6$ leaves (including) and $59.7\%$ for trees up to $10$ in our simulated dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge