A formula for the area of a triangle: Useless, but explicitly in Deep Sets form

Any permutation-invariant function of data points $\vec{r}_i$ can be written in the form $\rho(\sum_i\phi(\vec{r}_i))$ for suitable functions $\rho$ and $\phi$. This form - known in the machine-learning literature as Deep Sets - also generates a map-reduce algorithm. The area of a triangle is a permutation-invariant function of the locations $\vec{r}_i$ of the three corners $1\leq i\leq 3$. We find the polynomial formula for the area of a triangle that is explicitly in Deep Sets form. This project was motivated by questions about the fundamental computational complexity of $n$-point statistics in cosmology; that said, no insights of any kind were gained from these results.

Accelerated Computation of a High Dimensional Kolmogorov-Smirnov Distance

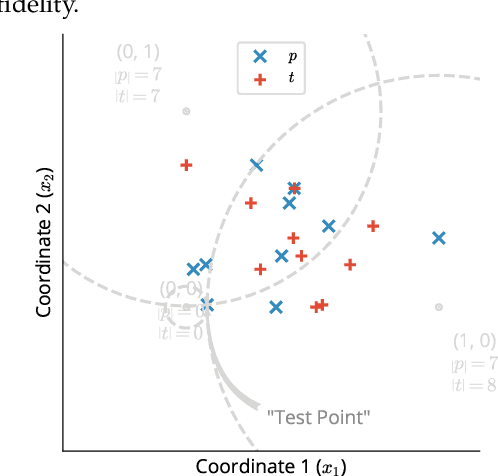
Statistical testing is widespread and critical for a variety of scientific disciplines. The advent of machine learning and the increase of computing power has increased the interest in the analysis and statistical testing of multidimensional data. We extend the powerful Kolmogorov-Smirnov two sample test to a high dimensional form in a similar manner to Fasano (Fasano, 1987). We call our result the d-dimensional Kolmogorov-Smirnov test (ddKS) and provide three novel contributions therewith: we develop an analytical equation for the significance of a given ddKS score, we provide an algorithm for computation of ddKS on modern computing hardware that is of constant time complexity for small sample sizes and dimensions, and we provide two approximate calculations of ddKS: one that reduces the time complexity to linear at larger sample sizes, and another that reduces the time complexity to linear with increasing dimension. We perform power analysis of ddKS and its approximations on a corpus of datasets and compare to other common high dimensional two sample tests and distances: Hotelling's T^2 test and Kullback-Leibler divergence. Our ddKS test performs well for all datasets, dimensions, and sizes tested, whereas the other tests and distances fail to reject the null hypothesis on at least one dataset. We therefore conclude that ddKS is a powerful multidimensional two sample test for general use, and can be calculated in a fast and efficient manner using our parallel or approximate methods. Open source implementations of all methods described in this work are located at https://github.com/pnnl/ddks.