SEO: Safety-Aware Energy Optimization Framework for Multi-Sensor Neural Controllers at the Edge

Runtime energy management has become quintessential for multi-sensor autonomous systems at the edge for achieving high performance given the platform constraints. Typical for such systems, however, is to have their controllers designed with formal guarantees on safety that precede in priority such optimizations, which in turn limits their application in real settings. In this paper, we propose a novel energy optimization framework that is aware of the autonomous system's safety state, and leverages it to regulate the application of energy optimization methods so that the system's formal safety properties are preserved. In particular, through the formal characterization of a system's safety state as a dynamic processing deadline, the computing workloads of the underlying models can be adapted accordingly. For our experiments, we model two popular runtime energy optimization methods, offloading and gating, and simulate an autonomous driving system (ADS) use-case in the CARLA simulation environment with performance characterizations obtained from the standard Nvidia Drive PX2 ADS platform. Our results demonstrate that through a formal awareness of the perceived risks in the test case scenario, energy efficiency gains are still achieved (reaching 89.9%) while maintaining the desired safety properties.

EnergyShield: Provably-Safe Offloading of Neural Network Controllers for Energy Efficiency

To mitigate the high energy demand of Neural Network (NN) based Autonomous Driving Systems (ADSs), we consider the problem of offloading NN controllers from the ADS to nearby edge-computing infrastructure, but in such a way that formal vehicle safety properties are guaranteed. In particular, we propose the EnergyShield framework, which repurposes a controller ''shield'' as a low-power runtime safety monitor for the ADS vehicle. Specifically, the shield in EnergyShield provides not only safety interventions but also a formal, state-based quantification of the tolerable edge response time before vehicle safety is compromised. Using EnergyShield, an ADS can then save energy by wirelessly offloading NN computations to edge computers, while still maintaining a formal guarantee of safety until it receives a response (on-vehicle hardware provides a just-in-time fail safe). To validate the benefits of EnergyShield, we implemented and tested it in the Carla simulation environment. Our results show that EnergyShield maintains safe vehicle operation while providing significant energy savings compared to on-vehicle NN evaluation: from 24% to 54% less energy across a range of wireless conditions and edge delays.

Polynomial-Time Reachability for LTI Systems with Two-Level Lattice Neural Network Controllers

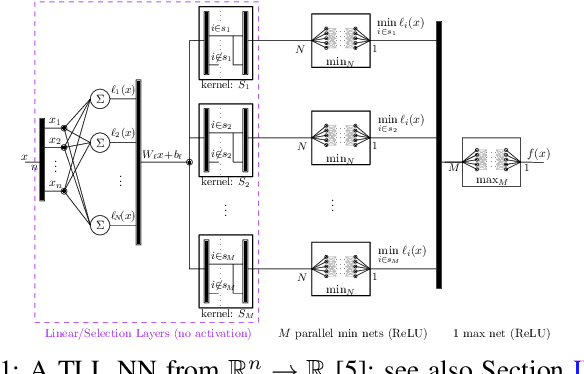
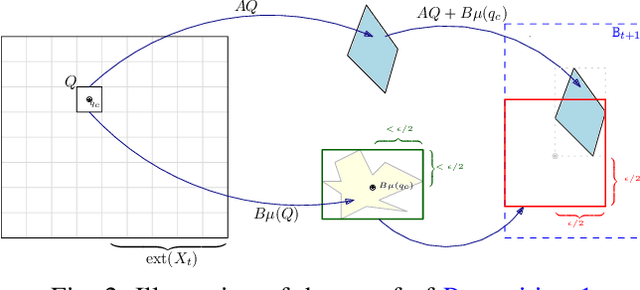
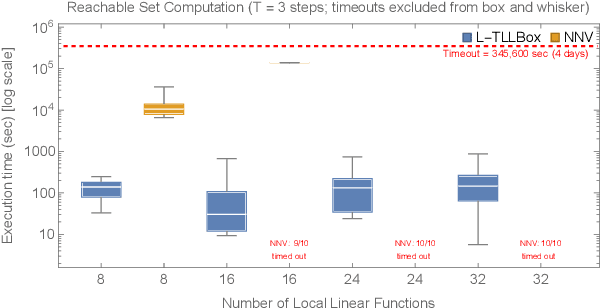
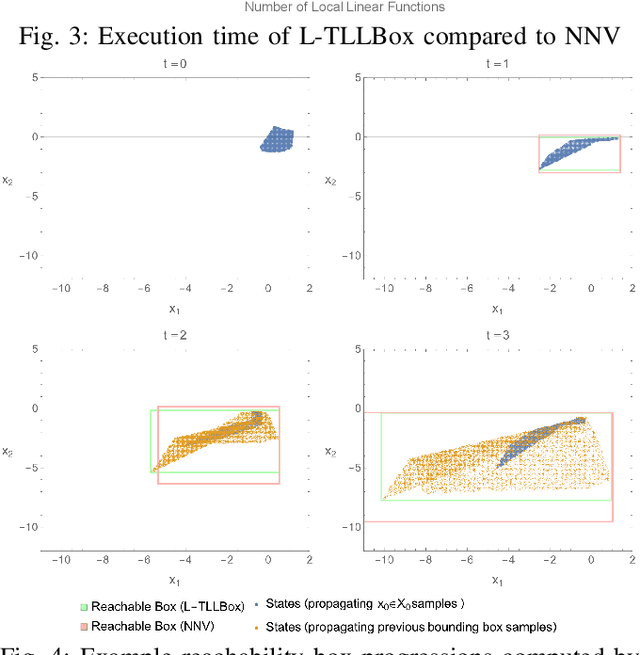
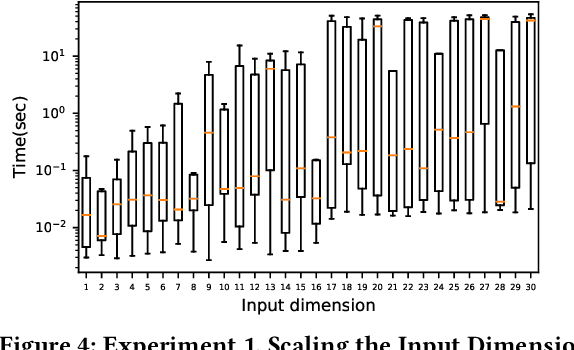
In this paper, we consider the computational complexity of bounding the reachable set of a Linear Time-Invariant (LTI) system controlled by a Rectified Linear Unit (ReLU) Two-Level Lattice (TLL) Neural Network (NN) controller. In particular, we show that for such a system and controller, it is possible to compute the exact one-step reachable set in polynomial time in the size of the size of the TLL NN controller (number of neurons). Additionally, we show that it is possible to obtain a tight bounding box of the reachable set via two polynomial-time methods: one with polynomial complexity in the size of the TLL and the other with polynomial complexity in the Lipschitz constant of the controller and other problem parameters. Crucially, the smaller of the two can be decided in polynomial time for non-degenerate TLL NNs. Finally, we propose a pragmatic algorithm that adaptively combines the benefits of (semi-)exact reachability and approximate reachability, which we call L-TLLBox. We evaluate L-TLLBox with an empirical comparison to a state-of-the-art NN controller reachability tool. In these experiments, L-TLLBox was able to complete reachability analysis as much as 5000x faster than this tool on the same network/system, while producing reach boxes that were from 0.08 to 1.42 times the area.

Fast BATLLNN: Fast Box Analysis of Two-Level Lattice Neural Networks

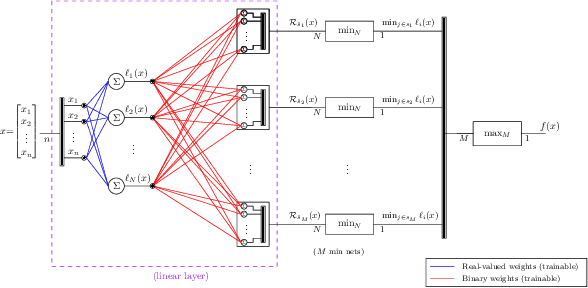
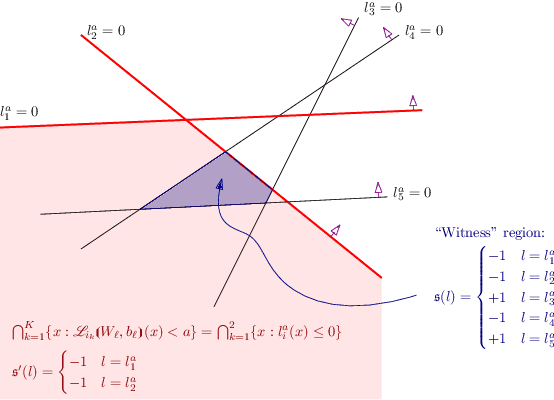
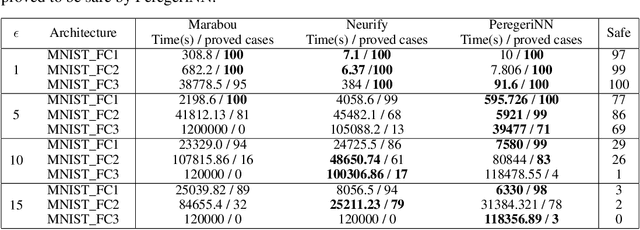
In this paper, we present the tool Fast Box Analysis of Two-Level Lattice Neural Networks (Fast BATLLNN) as a fast verifier of box-like output constraints for Two-Level Lattice (TLL) Neural Networks (NNs). In particular, Fast BATLLNN can verify whether the output of a given TLL NN always lies within a specified hyper-rectangle whenever its input constrained to a specified convex polytope (not necessarily a hyper-rectangle). Fast BATLLNN uses the unique semantics of the TLL architecture and the decoupled nature of box-like output constraints to dramatically improve verification performance relative to known polynomial-time verification algorithms for TLLs with generic polytopic output constraints. In this paper, we evaluate the performance and scalability of Fast BATLLNN, both in its own right and compared to state-of-the-art NN verifiers applied to TLL NNs. Fast BATLLNN compares very favorably to even the fastest NN verifiers, completing our synthetic TLL test bench more than 400x faster than its nearest competitor.

Assured Neural Network Architectures for Control and Identification of Nonlinear Systems

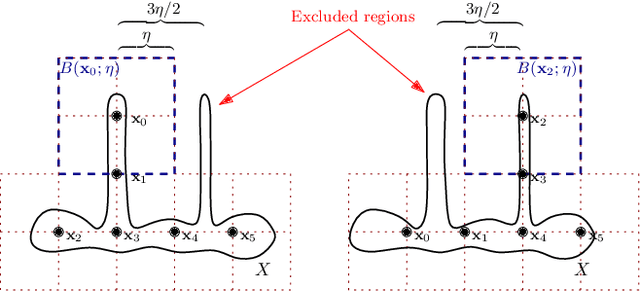
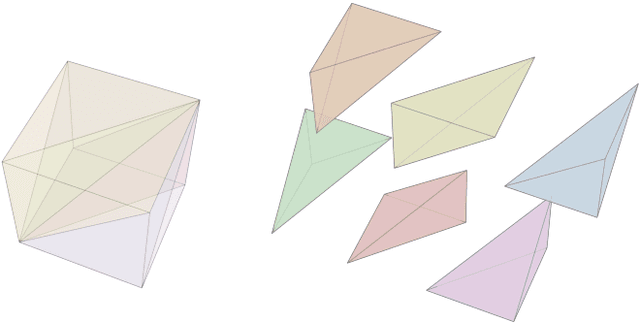
In this paper, we consider the problem of automatically designing a Rectified Linear Unit (ReLU) Neural Network (NN) architecture (number of layers and number of neurons per layer) with the assurance that it is sufficiently parametrized to control a nonlinear system; i.e. control the system to satisfy a given formal specification. This is unlike current techniques, which provide no assurances on the resultant architecture. Moreover, our approach requires only limited knowledge of the underlying nonlinear system and specification. We assume only that the specification can be satisfied by a Lipschitz-continuous controller with a known bound on its Lipschitz constant; the specific controller need not be known. From this assumption, we bound the number of affine functions needed to construct a Continuous Piecewise Affine (CPWA) function that can approximate any Lipschitz-continuous controller that satisfies the specification. Then we connect this CPWA to a NN architecture using the authors' recent results on the Two-Level Lattice (TLL) NN architecture; the TLL architecture was shown to be parameterized by the number of affine functions present in the CPWA function it realizes.

Safe-by-Repair: A Convex Optimization Approach for Repairing Unsafe Two-Level Lattice Neural Network Controllers

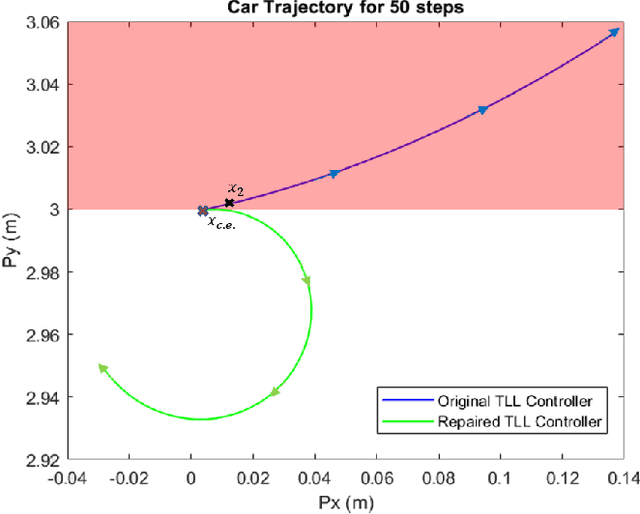
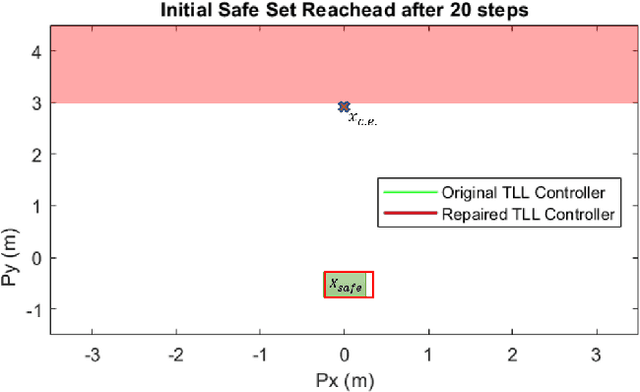
In this paper, we consider the problem of repairing a data-trained Rectified Linear Unit (ReLU) Neural Network (NN) controller for a discrete-time, input-affine system. That is we assume that such a NN controller is available, and we seek to repair unsafe closed-loop behavior at one known "counterexample" state while simultaneously preserving a notion of safe closed-loop behavior on a separate, verified set of states. To this end, we further assume that the NN controller has a Two-Level Lattice (TLL) architecture, and exhibit an algorithm that can systematically and efficiently repair such an network. Facilitated by this choice, our approach uses the unique semantics of the TLL architecture to divide the repair problem into two significantly decoupled sub-problems, one of which is concerned with repairing the un-safe counterexample -- and hence is essentially of local scope -- and the other of which ensures that the repairs are realized in the output of the network -- and hence is essentially of global scope. We then show that one set of sufficient conditions for solving each these sub-problems can be cast as a convex feasibility problem, and this allows us to formulate the TLL repair problem as two separate, but significantly decoupled, convex optimization problems. Finally, we evaluate our algorithm on a TLL controller on a simple dynamical model of a four-wheel-car.

Bounding the Complexity of Formally Verifying Neural Networks: A Geometric Approach

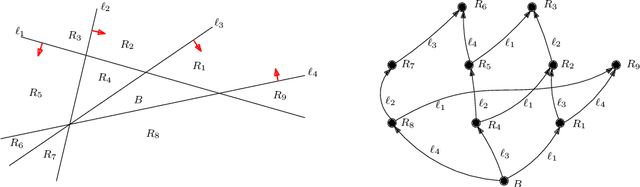
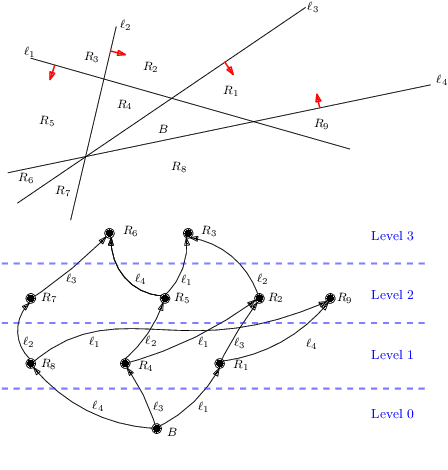
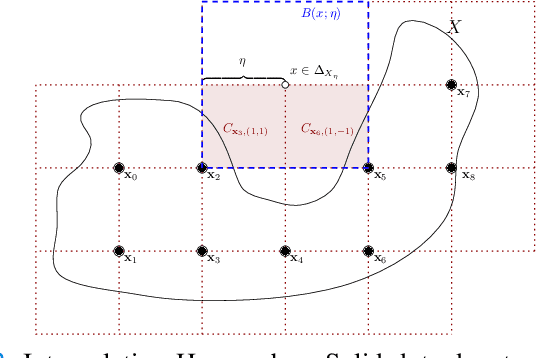
In this paper, we consider the computational complexity of formally verifying the input/output behavior of Rectified Linear Unit (ReLU) Neural Networks (NNs): that is we consider the complexity of determining whether the output of a NN lies in a specific convex polytopic region (in its range) whenever its input lies in a specific polytopic region (in its domain). Specifically, we show that for two different NN architectures -- shallow NNs and Two-Level Lattice (TLL) NNs -- the verification problem with polytopic constraints is polynomial in the number of neurons in the NN to be verified, when all other aspects of the verification problem held fixed. We achieve these complexity results by exhibiting an explicit verification algorithm for each type of architecture. Nevertheless, both algorithms share a commonality in structure. First, they efficiently translate the NN parameters into a partitioning of the NN's input space by means of hyperplanes; this has the effect of partitioning the original verification problem into sub-verification problems derived from the geometry of the NN itself. These partitionings have two further important properties. First, the number of these hyperplanes is polynomially related to the number of neurons, and hence so is the number of sub-verification problems. Second, each of the subproblems is solvable in polynomial time by means of a Linear Program (LP). Thus, to attain an overall polynomial time algorithm for the original verification problem, it is only necessary to enumerate these subproblems in polynomial time. For this, we also contribute a novel algorithm to enumerate the regions in a hyperplane arrangement in polynomial time; our algorithm is based on a poset ordering of the regions for which poset successors are polynomially easy to compute.

Effective Formal Verification of Neural Networks using the Geometry of Linear Regions

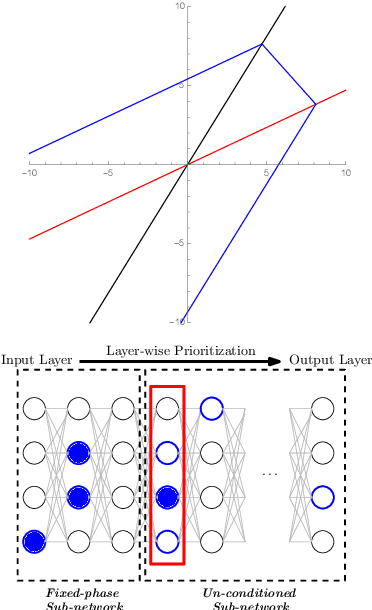
Neural Networks (NNs) have increasingly apparent safety implications commensurate with their proliferation in real-world applications: both unanticipated as well as adversarial misclassifications can result in fatal outcomes. As a consequence, techniques of formal verification have been recognized as crucial to the design and deployment of safe NNs. In this paper, we introduce a new approach to formally verify the most commonly considered safety specification for ReLU NNs -- i.e. polytopic specifications on the input and output of the network. Like some other approaches, ours uses a relaxed convex program to mitigate the combinatorial complexity of the problem. However, unique in our approach is the way we exploit the geometry of neuronal activation regions to further prune the search space of relaxed neuron activations. In particular, conditioning on neurons from input layer to output layer, we can regard each relaxed neuron as having the simplest possible geometry for its activation region: a half-space.This paradigm can be leveraged to create a verification algorithm that is not only faster in general than competing approaches, but is also able to verify considerably more safety properties. For example, our approach completes the standard MNIST verification test bench 2.7-50 times faster than competing algorithms while still proving 14-30% more properties. We also used our framework to verify the safety of a neural network controlled autonomous robot in a structured environment, and observed a 1900 times speed up compared to existing methods.

ShieldNN: A Provably Safe NN Filter for Unsafe NN Controllers

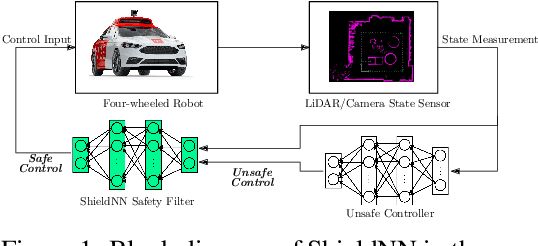
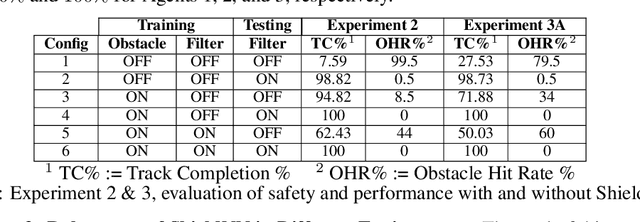
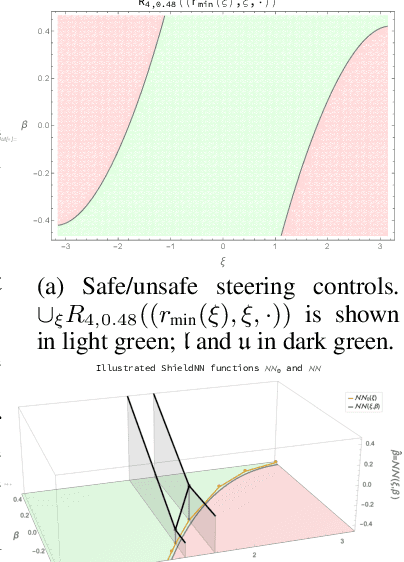
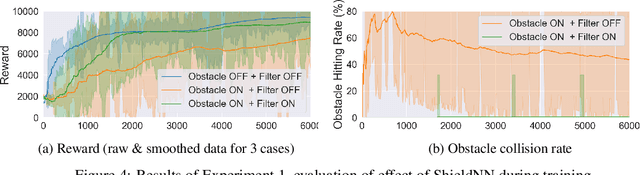
In this paper, we consider the problem of creating a safe-by-design Rectified Linear Unit (ReLU) Neural Network (NN), which, when composed with an arbitrary control NN, makes the composition provably safe. In particular, we propose an algorithm to synthesize such NN filters that safely correct control inputs generated for the continuous-time Kinematic Bicycle Model (KBM). ShieldNN contains two main novel contributions: first, it is based on a novel Barrier Function (BF) for the KBM model; and second, it is itself a provably sound algorithm that leverages this BF to a design a safety filter NN with safety guarantees. Moreover, since the KBM is known to well approximate the dynamics of four-wheeled vehicles, we show the efficacy of ShieldNN filters in CARLA simulations of four-wheeled vehicles. In particular, we examined the effect of ShieldNN filters on Deep Reinforcement Learning trained controllers in the presence of individual pedestrian obstacles. The safety properties of ShieldNN were borne out in our experiments: the ShieldNN filter reduced the number of obstacle collisions by 99.4%-100%. Furthermore, we also studied the effect of incorporating ShieldNN during training: for a constant number of episodes, 28% less reward was observed when ShieldNN wasn't used during training. This suggests that ShieldNN has the further property of improving sample efficiency during RL training.

Two-Level Lattice Neural Network Architectures for Control of Nonlinear Systems

In this paper, we consider the problem of automatically designing a Rectified Linear Unit (ReLU) Neural Network (NN) architecture (number of layers and number of neurons per layer) with the guarantee that it is sufficiently parametrized to control a nonlinear system. Whereas current state-of-the-art techniques are based on hand-picked architectures or heuristic based search to find such NN architectures, our approach exploits the given model of the system to design an architecture; as a result, we provide a guarantee that the resulting NN architecture is sufficient to implement a controller that satisfies an achievable specification. Our approach exploits two basic ideas. First, assuming that the system can be controlled by an unknown Lipschitz-continuous state-feedback controller with some Lipschitz constant upper-bounded by $K_\text{cont}$, we bound the number of affine functions needed to construct a Continuous Piecewise Affine (CPWA) function that can approximate the unknown Lipschitz-continuous controller. Second, we utilize the authors' recent results on a novel NN architecture named as the Two-Level Lattice (TLL) NN architecture, which was shown to be capable of implementing any CPWA function just from the knowledge of the number of affine functions that compromises this CPWA function.