Assured Neural Network Architectures for Control and Identification of Nonlinear Systems

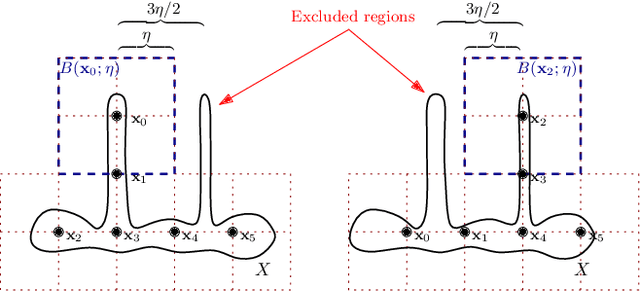
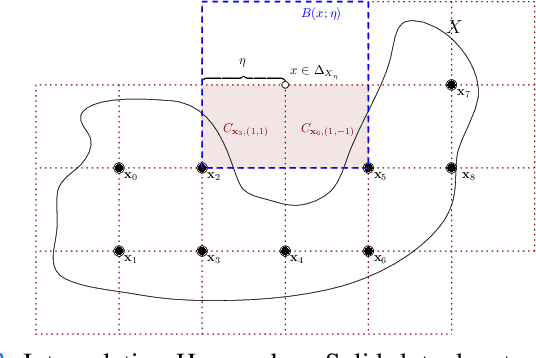
In this paper, we consider the problem of automatically designing a Rectified Linear Unit (ReLU) Neural Network (NN) architecture (number of layers and number of neurons per layer) with the assurance that it is sufficiently parametrized to control a nonlinear system; i.e. control the system to satisfy a given formal specification. This is unlike current techniques, which provide no assurances on the resultant architecture. Moreover, our approach requires only limited knowledge of the underlying nonlinear system and specification. We assume only that the specification can be satisfied by a Lipschitz-continuous controller with a known bound on its Lipschitz constant; the specific controller need not be known. From this assumption, we bound the number of affine functions needed to construct a Continuous Piecewise Affine (CPWA) function that can approximate any Lipschitz-continuous controller that satisfies the specification. Then we connect this CPWA to a NN architecture using the authors' recent results on the Two-Level Lattice (TLL) NN architecture; the TLL architecture was shown to be parameterized by the number of affine functions present in the CPWA function it realizes.