Bounding the Complexity of Formally Verifying Neural Networks: A Geometric Approach

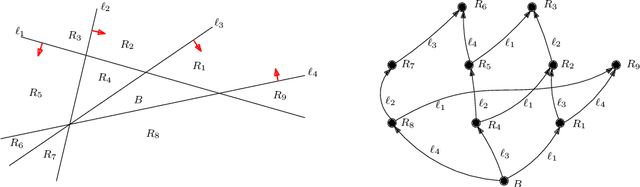
In this paper, we consider the computational complexity of formally verifying the input/output behavior of Rectified Linear Unit (ReLU) Neural Networks (NNs): that is we consider the complexity of determining whether the output of a NN lies in a specific convex polytopic region (in its range) whenever its input lies in a specific polytopic region (in its domain). Specifically, we show that for two different NN architectures -- shallow NNs and Two-Level Lattice (TLL) NNs -- the verification problem with polytopic constraints is polynomial in the number of neurons in the NN to be verified, when all other aspects of the verification problem held fixed. We achieve these complexity results by exhibiting an explicit verification algorithm for each type of architecture. Nevertheless, both algorithms share a commonality in structure. First, they efficiently translate the NN parameters into a partitioning of the NN's input space by means of hyperplanes; this has the effect of partitioning the original verification problem into sub-verification problems derived from the geometry of the NN itself. These partitionings have two further important properties. First, the number of these hyperplanes is polynomially related to the number of neurons, and hence so is the number of sub-verification problems. Second, each of the subproblems is solvable in polynomial time by means of a Linear Program (LP). Thus, to attain an overall polynomial time algorithm for the original verification problem, it is only necessary to enumerate these subproblems in polynomial time. For this, we also contribute a novel algorithm to enumerate the regions in a hyperplane arrangement in polynomial time; our algorithm is based on a poset ordering of the regions for which poset successors are polynomially easy to compute.